Tangential Circles and a Line

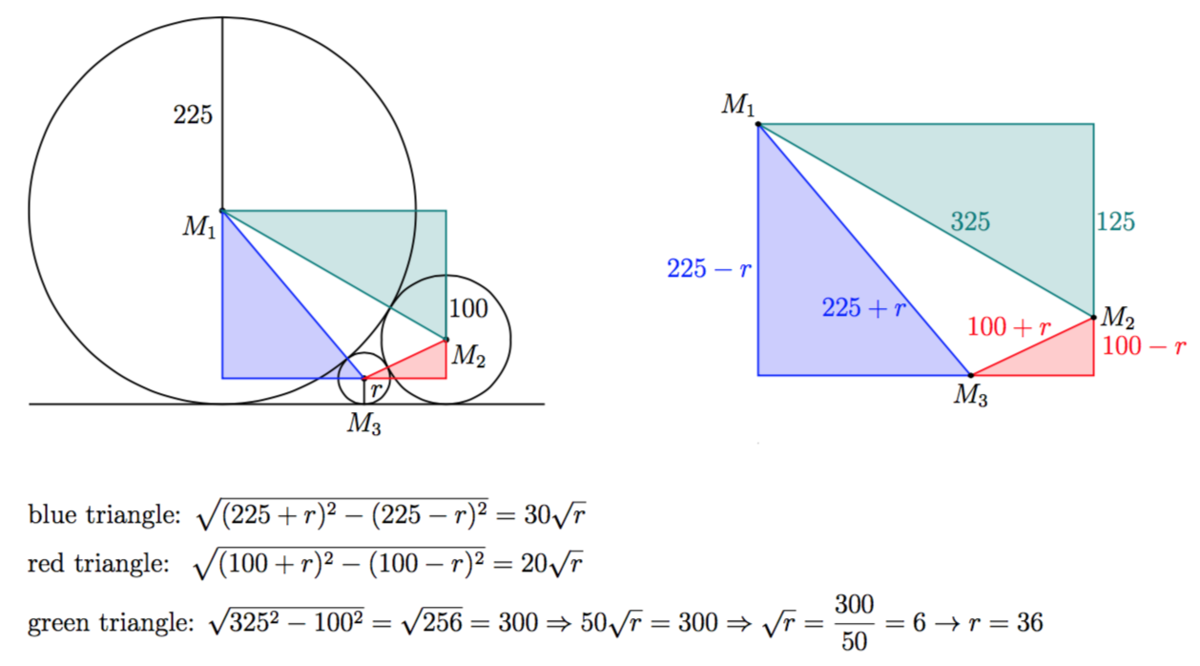
Three right triangles can be constructed, where each hypotenuse is the segment between the centers of two circles and therefore the sum of the two radii of those two circles, and each vertical leg is the difference between the two radii of those same two circles, as pictured below:

In the blue right triangle where the hypotenuse is between the center of the largest circle with a radius of 225 and the center of the medium circle with a radius of 100, the hypotenuse is 225 + 100 = 325, and the vertical leg is 225 – 100 = 125, which means the horizontal leg z is z = $\sqrt{325^2 - 125^2}$ by the Pythagorean Theorem, and simplifies to z = 300.

In the green right triangle where the hypotenuse is between the center of the largest circle with a radius of 225 and the center of the smallest circle with an unknown radius r, the hypotenuse is 225 + r, and the vertical leg is 225 – r, which means the horizontal leg x is x = $\sqrt{(225 + r)^2 - (225 - r)^2}$ by the Pythagorean Theorem, and simplifies to x = $\sqrt{((225 + r) + (225 - r))((225 + r) - (225 - r))}$ = $\sqrt{450 \cdot 2r}$ = $\sqrt{900r}$ = $30\sqrt{r}$ .

In the red right triangle where the hypotenuse is between the center of the medium circle with a radius of 100 and the center of the smallest circle with an unknown radius r, the hypotenuse is 100 + r, and the vertical leg is 100 – r, which means the horizontal leg y is y = $\sqrt{(100 + r)^2 - (100 - r)^2}$ by the Pythagorean Theorem, and simplifies to y = $\sqrt{((100 + r) + (100 - r))((100 + r) - (100 - r))}$ = $\sqrt{200 \cdot 2r}$ = $\sqrt{400r}$ = $20\sqrt{r}$ .

The two smaller horizontal segments x and y add up to the larger horizontal segment z, so x + y = z, and substituting x = $30\sqrt{r}$ , y = $20\sqrt{r}$ and z = 300 gives $30\sqrt{r}$ + $20\sqrt{r}$ = 300. This means $50\sqrt{r}$ = 300, and $\sqrt{r}$ = 6, and r = 36.