This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
How did you get 36? is 4+2x2? Where is that from? What are the last four triangles you add?
Log in to reply
To count the number of rectangles in a 3 × 3 grid, we have to choose 2 horizontal lines (out of 4) and 2 vertical lines (out of 4). Thus, there are ( 2 4 ) × ( 2 4 ) = 6 × 6 = 3 6 such rectangles.
We then have to add the rectangles which include the top most rectangle. This would be any of the vertical rectangles through the middle, of which there are 4 of them.
Log in to reply
what is that (4/2) or some thing else. 4/2 =2 how it is 6. please elaborate the calculation.
Log in to reply
@Kiran Waychal – ( 2 4 ) is the mathematical notation for "4 choose 2". It is calculated as 2 × 1 4 × 3 = 2 1 2 = 6 .
Read up on Combinations .
I am able to count 44 rectangles.
Log in to reply
uhh i messed up and forgot the extra rectangle, but how are you getting 44 , are you counting by hand or as @Chung Kevin did?
For this question, if you use Casework like Curtis did, then you have to be very very careful to list them out clearly, to ensure that you have counted the rectangles exactly once.
I like his format of "list out all the different types of rectangles, and ensure that we have the correct count for them". If you did that, you can check against his list and see what values you obtain.
Log in to reply
Actually I too used casework but I by mistake I counted 2*2 twice that led to an error.
Log in to reply
@Ankit Kumar Jain – Yes, when I first set this problem, I counted 38 rectangles. I didn't like how "random" it was, so I tried to find a "better" solution. I like my approach.
today i need some tutor :D
You could use longer method with casework, where the length of the rectangles is denoted as y and the width as x such that we group them up as follows: x y = 1 0 , x . 2 y = 7 , x . 3 y = 4 , x . 4 y = 1 2 x . y = 6 , 2 x . 2 y = 4 , 2 x . 3 y = 2 3 x . y = 3 , 3 x . 2 y = 2 , 3 x . 3 y = 1 ∴ n u m b e r o f r e c t a n g l e s = 4 0
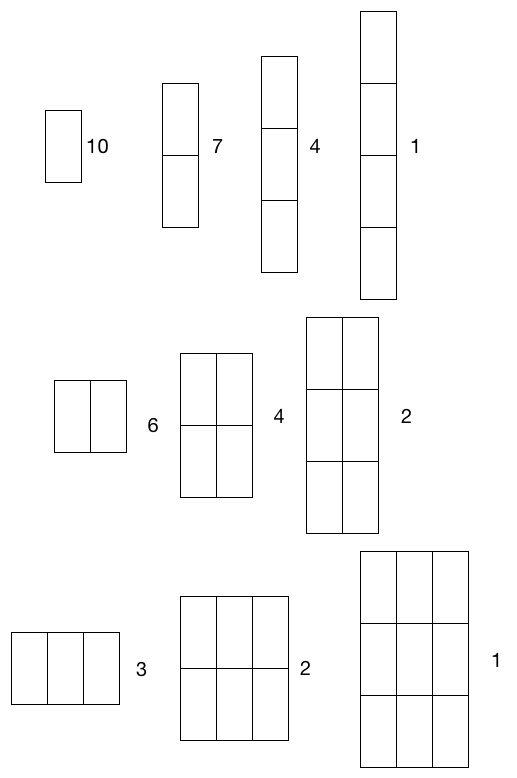
I attached a graphic listing out the rectangles and number of them. I think that makes it easier to visually see and confirm that your values are correct.
It is very easy to miss / double count one or two rectangles here and there.
That was my first approach, but then I miscounted because I forgot one of them. That's why I tried to come up with a better approach.
1 x 1 ........................ 10
1 x 2 ........................13
1 x 3 ........................7
1 x 4 ...........................1
2 x 2 .........................4
2 x 3 ..........................4
3 x 3 ..........................1
Number of rectangles = 40
If you look at the rectangles' vertices ( 2 4 ) would represent all possible rectangles formed by choosing 2 vertices out of the given 4 points from the length and width of the 3 by 3 rectangle on the bottom (which is composed of 4 vertices on each side).
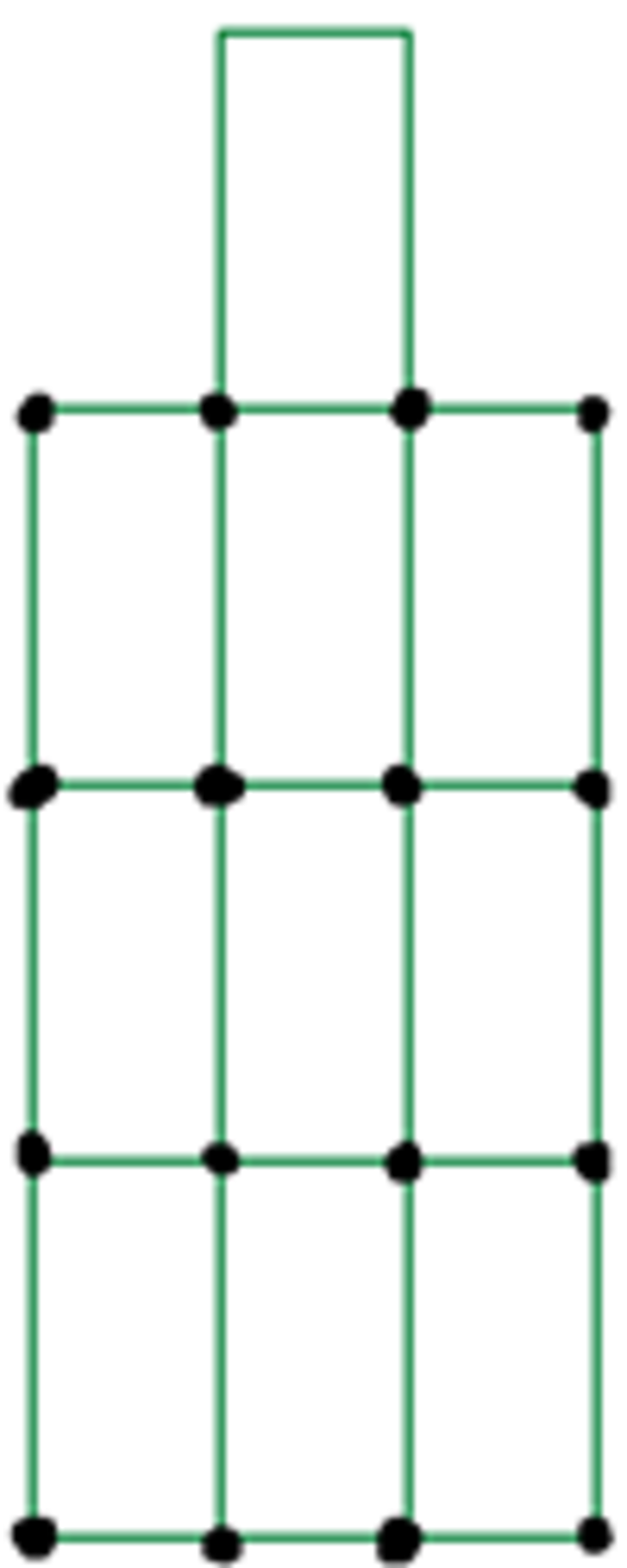
( 2 4 ) is equal to 6, so ( 2 4 ) × ( 2 4 ) gives 36.
Plus the top middle rectangle which contains 4 possible rectangles, the answer is 36 + 4 rectangles.
Nice approach, just like mine :)
Gut feeling dictates - rectangle below has 9 sections and it is quite probably that rectangle count would be dividable by 3. It could be 39 for instance. 1 more above rounds it up to 40.
Why would it be divisible by 3?
Why would you choose to just add 1? Notice that there are 4 rectangles which involve the top most one, and not just 1 rectangle.

We could count all of the rectangles and hope that we got all of them, but that's tedious / could lead to an error.
Alternatively, we know that in the 3 × 3 grid, there are going to be ( 2 4 ) × ( 2 4 ) = 3 6 rectangles. We then add those which include the top most rectangle, and there are 4 of them.
Hence, there are a total of 3 6 + 4 = 4 0 rectangles.