Teetering Book Tower
Joey has an infinite number of identical books that are rigid and perfectly rectangular. He places them all in a stack on the edge of a table.
What is the maximum distance (parallel to the ground) that the edge of the top book can get from the edge of the table without falling over?
Assume the gravitational field is vertical and uniform.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
... (sigh) ... while I like the explanation, I wanted to use it to create a picture of a stack of dominoes where the top domino is clearly beyond the edge of the table. I have not been able to do this! The best I can do is have the top domino approach being halfway over the edge. Can anyone post a picture of a stack of dominoes (or books or whatever) where the top object is clearly beyond the edge? On the other hand, can anyone explain why this theoretical solution cannot actually be constructed. Thanks. (color me curious)
Log in to reply
Log in to reply
... right ... so I wanted to create a real stack of teetering dominoes. The problem seems to be that my dominoes are unaware of my expectations for them. For more stability, I decided to stack dominoes slightly less than the optimal fractions given in the theoretical solutions. In one trial I even used rubber cement to bind the dominoes together, possibly eliminating any instability related to angular momentum effects for each domino. The picture below ( at PhotoBucket ) is the best I've been able to do. The dominoes are not cemented and the top (i.e. 7th) domino is more than halfway beyond the edge of the table. In all of my trials with various numbers of dominoes, where the top block extends more than halfway beyond the table edge, adding another domino at any position (i.e. even directly on top with no offset) would cause the stack to topple over. My challenge: provide a picture to prove that you can stack books (or bricks or dominoes or playing cards, etc.) such that the top object is positioned beyond the edge of the table!

Log in to reply
@David Hairston – I've just done it it with five playing cards (and no glue or sneaky cheats). The trick is not to be too ambitious with the first cards. If you look at my solution you will see that for a stable configuration reaching beyond the edge of the table, the bottom card should project a little less than a tenth of a card length, the next a little less than an eighth, the next a little less than a sixth, the next a little less than a quarter and the top card a little less than a half. It is easier to construct the tower away from the edge of the table, starting by overlaying the second card by a little less than an eighth of a card length. When the tower is built carefully slide the whole structure until the bottom card projects by a little less than a tenth and the top card is just beyond the edge.
It looks amazing and isn't hard to do.
good luck!
Log in to reply
@Peter Macgregor
–
 Wow, with cards it is WAY easier with dominos, I experimented with dominos for about 20 minutes and started to lose faith in the answer. Even taking into consideration friction and the non-rigidity of cards, the fact that these are hanging more than an extra card past the edge is pretty strong support for the answer.
Wow, with cards it is WAY easier with dominos, I experimented with dominos for about 20 minutes and started to lose faith in the answer. Even taking into consideration friction and the non-rigidity of cards, the fact that these are hanging more than an extra card past the edge is pretty strong support for the answer.
Log in to reply
@Alex Li – Hi Alex -
Thanks for posting the amazing picture. it should go a long way to convincing the doubters!
cheers!
@Alex Li – Many possible explanations. 1) dishonesty: cards are glued. I seriously doubt this can be reproduced (ie: scientific method). 2) Static electricity 3) etc..
Log in to reply
@Gilles Gagnon – Haha well I promise it's not dishonestly- of all the things to lie about, why would I lie about that? Anyways you can try it for yourself, with cards its very easy to do. Sometimes the answer is hard to believe but the harder it is to believe, the more you learn from it.
@Peter Macgregor – okay ... so I tried this with playing cards and I was able to hang a card beyond the table edge. Yay! I was also able to find some ancient Time-Life books that were remarkably the same size (i.e. all of them are 200 pages). I suspect that the dimensions may be a factor. In any case, I was also able to hang a book over the table edge. Double yay!! Unfortunately, my dominoes refuse to believe so I have been unable to reproduce these results with dominoes. Sigh. I would still like to see a picture of bricks that reproduces these results. Cheers! (suspenseful music) Oh ... I should point out that even with a whole deck of cards, I was unable to hang a card more than 5-10% beyond the edge of the table ... so a picture of this phenomenon would be really cool, too! (orchestra plays marching band music ...)
My pictures ( at PhotoBucket ):
Teeter Cards:

Teeter Books:

Thumbnail of a video that explains it: https://i.ytimg.com/vi/EegG5TPL29c/0.jpg
Video: https://www.youtube.com/watch?v=CdhuVhWTSMI
While I initially got this problem wrong, I came around. And I thought of another scenario that might make it easier for others to get 'over the hump'.
Imagine a solid object of constant density similar in shape to the horn a bull with a flat base, or an offset triangular obelisk. No one would be surprised to see that the obelisk could be placed at the edge of the table such that the tip overhanging the edge without the obelisk falling over. In fact, you could move the obelisk over the edge of the table up the the point that the center of gravity of the obelisk lies over the edge without it falling.
 diagram
diagram
Now, to increase the distance the tip extends beyond the table, simply make a bigger obelisk! Ignoring issues like how much weight the table can support, the tip of the obelisk could extend past the table any arbitrary distance by simply making it big enough so that the tip reaches the desired distance from the table edge with the object's center of gravity still on the other side.
Now, I hear some of you saying that this scenario is wrong because the obelisk is a solid object, where the stack of books is not. In fact, ignoring things like air currents or sliding, a stack of books, cards, or dominoes will behave the same as the obelisk. To illustrate this, we'll borrow from calculus. Imagine you could divide the obelisk with a laser using a horizontal cut some arbitrary point between the base and the tip. No matter where you made the cut, the two parts would not fall as long as the parts remain in the same position they were in prior to the cut. Now cut those parts into two parts. Same result. In fact, you could cut the obelisk into an arbitrary number of slices and it would be just as stable as when it was a solid object (ignoring air, mischievous siblings, and earthquakes, etc.).
Log in to reply
This obelisk becomes narrower as you go up, so it is a bit different than the setup in this question. Still, this is a great example showing we can get as far as we want from the base of the edge by increasing the height sufficiently.
Very nice explanation! This solution not only shows the math, but helps create an intuitive sense of what is happening.
I disagree!
 check
check
Log in to reply
Is your point that the configuration in your drawing would fall over?
Log in to reply
Definitely!!!
Log in to reply
@Guiseppi Butel – The object would indeed fall, but this is not the only possible configuration of books.
Log in to reply
@Alex Li
–
I now agree with the answer.
 pic
pic
Log in to reply
@Guiseppi Butel – This looks like the record!
Wrong answer, because wrong assumptions. You can't assume the stack of books acts as one mass with one center of gravity. Each book has it's own pivot point that can cause a torque. As books are added above, the CG moves to the right until a given book at the bottom of the pile has more mass past the pivot point than it can support. Then it rotates around the pivot point, ie: it topples.
Log in to reply
The books are arranged such that for any book in the stack, the center of mass of all the books above it lies is not beyond the book itself. This ensures that the books don't topple.
This image shows the optimal solution for how the books can be stacked.
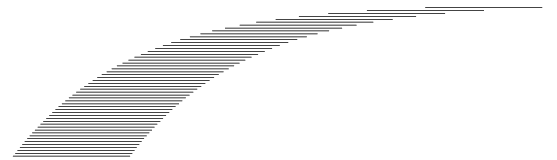
This approach, although very clever, arrives at an incorrect answer. The fault is not in the method of approach, but in simply calculating the centre of mass of each new "tower."
There is something wrong in your definition of "turning moments." I am assuming you mean torque (since there's no other thing related to moment here). You say that the new book has a turning moment (torque) of w/2. But with respect to what point?
Log in to reply
the new blocks, when they have just been introduced and are flush with the table produce a turning moment of 2 w w.r.t the edge of the table.
https://goo.gl/amcCjW
Link to an explanation of why there is a limit to far it can go.
Log in to reply
I believe that the problem with this is that you assume each block hangs over a constant amount. For example, with 5 blocks in Peter's construction, the torques from blocks 2 and 4 would not cancel out.
this is a lot of words
The question was how far, not how many books. Gravity and the fact the books are not glued together means as soon as the top book is a whole book beyond the edge it must topple. No matter how many books there are.
Log in to reply
The question was how far, not how many books.
True, but the total distance increases with the number of books.
Gravity and the fact the books are not glued together means as soon as the top book is a whole book beyond the edge it must topple. No matter how many books there are.
Any given book will topple if more than half of it is past the edge of the book below it. What you said isn't quite right.
If you can keep putting books at the top as far out as you want, then doesn't the center of gravity also move away from the table?
All the pictures that have been posted don't prove that the answer is "As far as he wants". Only that it might be that, or none of the answers listed.
Log in to reply
Here's an analysis of three books where the center of mass remains at the edge of the table as we continue to add books to the stack. This is for the case where the book on the bottom is 1 / 6 of a book length over the edge of the table, the middle book is 1 / 4 of a book length from the edge of the bottom book, and the top book is 1 / 2 of a book length from the edge of the middle book.
For the center of the mass on the bottom, we have r bottom = 2 1 × ( − 5 / 6 + 1 / 6 ) COM bottom book relative to edge of table = − 1 / 3
For the center of the mass in the middle, we have r middle = 2 1 × ( − 3 / 4 + 1 / 4 ) COM middle book relative to edge of bottom book + 1 / 6 = − 1 / 1 2 .
For the center of the mass on top, we have r top = 2 1 × ( − 1 / 2 + 1 / 2 ) COM middle book relative to edge of middle book + 1 / 6 + 1 / 4 = 5 / 1 2 .
And so ∑ r = r bottom + r middle + r top = − 4 / 1 2 − 1 / 1 2 + 5 / 1 2 = 0 .
Since the total center of mass it exactly at the edge of the table, this book stack stays up. Try to extend it by adding one more book to the bottom, so that it is 1 / 8 from the edge of the table. You should find that the center of mass stays at the edge of the table.
As we add further books to the system, with the n th one a distance 1 / 2 n from the edge of the one below it, the edge of the topmost book will get further and further from the edge of the table.
Mind... Blown...
Try it. Get a set of encyclopedias and experiment. My money says the books will fall off the table.
Oh I gotta appreciate your chutzpah, when you say you can make a bridge from you table to the moon just by using books, and use wrong physics arguments to justify it.
Just a quick sanity check. For any collection of books to not topple over the table, the center of mass should be on the table and not extending (to the right in the picture in problem) away from the table. Otherwise, the net torque from the corner will topple the books over, and there is nothing to balance it. (just doing the sanity check for 2 books, will invalidate your solution)
And then there is your infinite collection, with the center of mass protruding infinitely outside the table, causing infinite torque to topple the collection with nothing to balance it. Seriously !!! Am I missing something.
Log in to reply
Here's an easy one: show us the incorrect physics in the argument with three cards I just provided.
Log in to reply
I replied to your arguement.
Log in to reply
@Gaurav Sharma – I made a quick diagram adding up the weights on either side. I didn't get to calculate torque, but you can see there is more total weight on the table (right) side, which should eventually account for the torque as height increases. With the next layer, the weights get more disproportionate.

Here is also an image of someone building this with blocks.

The center of mass of the books on the table cannot lie beyond the edge of the table or the books will topple. As with @Peter Macgregor below, this means the top book cannot overhang the book beneath it by more than 2 1 .
Let's measure the center of mass of all our books from the right edge of the top book. The book underneath the top book can be offset by 2 1 to the left and the top book won't topple.
Now suppose we have n-1 books at center of mass c. Another book can be added beneath these books offset by 2 1 from the combined center of mass of n-1 books above so they don't topple. The center of mass of the n books is
n n − 1 * c + n 1 * (c+ 2 1 ) = c + 2 n 1
Writing out this sequence as @Peter Macgregor, the center of mass is the sum of 2 n 1 , which diverges as noted.
I don't have any pictures, but I used Jenga blocks to simulate. Jenga blocks are about 7.5 cm in length and about 1.5 cm thick. If n = the number of blocks above the base, the distance each block can be moved in without causing the tower to fall is about d = 4.65/n^0.89. With 8 blocks above the base, each block can be pushed in 0.7 cm without the tower collapsing. An indentation of 0.8 cm causes the tower to collapse. (That was fun!)
Log in to reply
That is a cool idea! Even though the math says you can push out the top book/block/CD case arbitrarily far, I feel like it would be hard to do it much past the length of the top item.
I wonder what the record is for actual books/blocks/CD cases. Now I wish I hadn't thrown all my CDs away!
I still have CDs. CDs measure 12.4 cm wide and 1.0 cm thick. The equation I got based on up to 7 CDs above the base was 7/n^0.78. Seven CDs above the base allowed for an indentation of 1.5 cm. A 1.6 cm indentation caused the CDs to topple.
Did you consider the moment force of distance*mass. I believe that the books will tip when the moment gets so large that it gets larger than the force of the book's resting mass. This is why the CD's and the Ginga blocks fell off in the live experiments in the comments above.
What a nice problem with a lovely counterintuitive answer! I hope my solution will convince you that the tower can indeed be extended as far as we please.
The answer seems so impossible because we imagine building the tower from the bottom up (naturally!). At some stage our tower of n books is tottering on the brink of collapse - so if the tower is already way out beyond the edge of the table how could we possibly add an ( n + 1 ) t h book without disaster? But imagine adding a new book to the bottom of the tower, and things are not quite so crazy. For instance suppose our tottering tower of n books is built to overhang the top of the ( n + 1 ) t h book which is sitting flush with the edge of the table. Now it does not seem so impossible that the new book could be pushed out a little from the edge of the table, and so the tower could be extended.
My solution is based on building up the tower by introducing new books one by one at the bottom, finding the centre of gravity of the new tower and then sliding the whole wobbly thing right a bit so that the centre of gravity is exactly over the edge of the table. In this way we can find the maximum extension beyond the edge of the table with n books. Suppose the books have length 1 and weight w, and start by sliding the first book out as far as it will go without falling, in other words shift it to the right by 2 1 .
Now introduce a new book underneath this book, the edge of the new book being flush with the table. The centre of gravity of this two book tower is to the left of the edge - but by how much? Well suppose the centre of gravity is a distance x from the edge. Then the turning moment (about the edge of the table) of the two block tower of weight 2w is 2wx. This turning moment is made up of two parts - the moment of the new book (which is 2 w ) and the moment of the first (top) book which is zero, because at the moment its centre of gravity is above the table's edge! Thus we have
2 w x = 2 w ⟹ x = 4 1
so we can get a two book tower tottering on the edge by sliding everything to the right by 4 1 .
Now introduce a third book underneath this two book tower, the edge of the new book being flush with the table. The centre of gravity of this three book tower is to the left of the edge - and again we ask, 'by how much?' Well suppose the tower's centre of gravity is a distance x from the edge. Then the turning moment (about the edge of the table) of the three block tower of weight 3w is 3wx. This turning moment is made up of two parts - the moment of the new book (which again is 2 w ) and the moment of the first two books which is zero, because the centre of gravity of the two book tower is, at this point in the construction, above the table's edge! Thus we have
3 w x = 2 w ⟹ x = 6 1
so we can get a three book tower tottering on the edge by sliding everything to the right by 6 1 .
By repeating the argument you can see that for n books the total distance slid to the right is
2 1 + 4 1 + 6 1 + ⋯ + 2 n 1 = 2 1 ( 1 + 2 1 + 3 1 + 4 1 + ⋯ + n 1 )
The series in brackets is the 'harmonic series' which does not converge - in other words it can be made as large as you like by taking enough terms.
Since the extension of the tower can be approximated by 2 1 ln ( n ) , and the logarithm grows so slowly, you will need whole libraries of books if you want to go more than a couple of metres from the edge of the table!