Tension in the Ring!

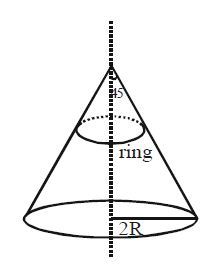A ring of mass $m$ , radius $R$ , cross sectional area $A$ and Young's modulus $Y$ is kept on a smooth cone of radius $2R$ and semi vertical angle $45°$ , as shown in the figure. Assume that the extension in the ring is small :-

$(A)$ The tension in the ring will be same throughout.

$(B)$ The tension in the ring will be independent of the radius of ring.

$(C)$ The extension in the ring will be $\frac{mgR}{AY}$

$(D)$ Elastic potential energy stored in the ring will be $\frac{m^2g^2R}{8\pi YA}$