Tension in the string

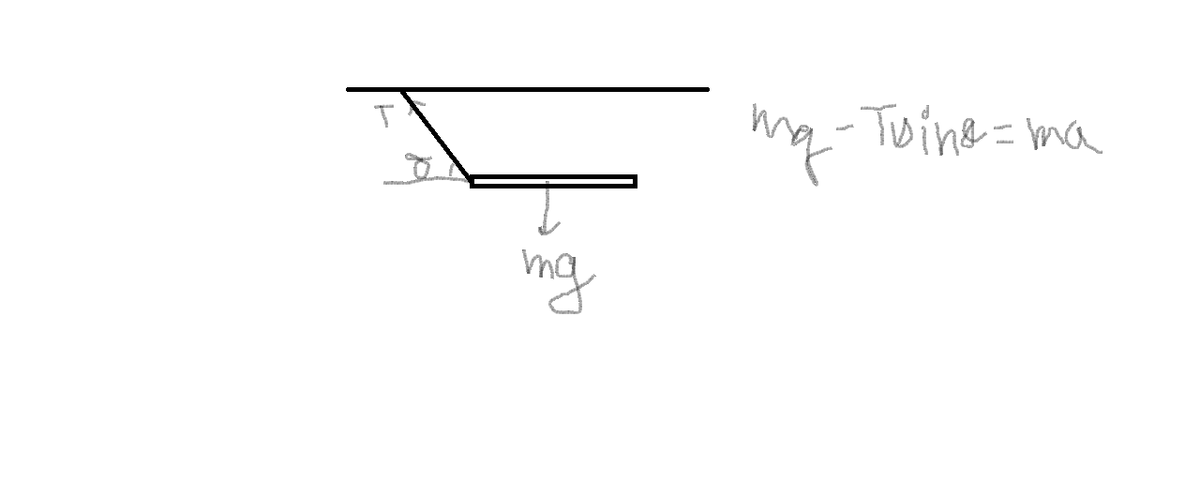
Consider the situation of the rod immediately after collision, make the following observations 1) centre of mass falls under gravity

2) Tension tends to oppose gravity and thus centre of mass does not free fall with acceleration 'g'

3) As the string is not normal to rod it has a non zero horizontal component which means centre of mass does not fall vertically downward

4) The string being inextensible (Constant length) means that as long as the string is not slack it will describe a circle about the pivot at the roof , thus the end of the rod just attached to the string describes an arc of the circle , thus moving PERPENDICULAR to the string.

5) And finally the torque about centre of mass is purely due to tension

Now lets state the above statements mathematically so that we can solve it

$mg\quad -\quad Tsin(\theta )=\quad m{ a }_{ y }\\ ---(1)\\ \\ Tcos(\theta )\quad =\quad m{ a }_{ x }\\ ---(2)\\ \\ and\quad \frac { l }{ 2 } Tsin(\theta )\quad =\quad I\alpha \\ ---(3)\\ \\ Now\quad lets\quad derive\quad the\quad constraing\quad equation\\ \\ All\quad components\quad on\quad the\quad rod\quad have\quad the\quad following\quad accelerations$

Now lets derive the constraing equation

any part of the rod experiences two accelerations,, one translation by virtue of com and one rotational by virtue of rotation about com

Thus the superposition of these two components gives the resultant acceleration at any point

For the end of rod just tied to string AP

the superposition of these accelerations give 0 net component along the string as the string is inextensible ,

the accelerations experienced by this part is

$\\ { a }_{ x }\quad along\quad horizontal\\ { a }_{ y }\quad along\quad vertical\\ (by\quad virtue\quad of\quad translation\quad of\quad com)\\ \\ and\quad \\ \\ \alpha \frac { l }{ 2 } \quad perpendicular\quad to\quad rod\\ \\ Thus\quad equating\quad components\quad along\quad string\quad to\quad 0\\ we\quad get\\ { a }_{ x }cos(\theta )\quad +\quad \alpha \frac { l }{ 2 } sin(\theta )\quad -\quad { a }_{ y }sin(\theta )\quad =\quad 0\\ \\ ---(4)\\$

Now solve these 4 equations to get

$T=\quad \frac { mg\quad sin(\theta ) }{ 3(sin(\theta ))^{ 2 }+1 }$

which on putting values you get the answer as 2.8

The constraint that I have imposed is only the acceleration of the point attached to the string along the string must be zero.Just after cutting let the tension be $T$ .then resolving $T$ into its components and taking the torque due to only the component perpendicular to the rod $(T/2)(L/2)=ML^2/12@$ so $@=3T/ML$ .( $@$ is the angular acceleration of the body).now we observe that the acceleration of point considered is $a(y)=(T/2M+@L/2-g)$ in the upward direction and $a(x)=(T√3/2M)$ in horizontal.so using the constraint $a(x)cos30+a(y)sin30=0$ .Now plugging the values of $a(x$ ) and $a(y)$ we get $T=2Mg/7$

also write torques about c.o.m , you get the ans as 2.823 !