Tetradecagon Area

Geometry Level 5

If the area of a regular unit polygon with $14$ sides can be expressed as:

$A \sin \cfrac{\pi}{7} + B \sin \cfrac{2\pi}{7} + C \sin \cfrac{3\pi}{7}$

for positive integers $A$ , $B$ , and $C$ , find $A + B + C$ .

Inspiration: (1) , (2)

The answer is 21.

3 solutions

Michael Huang
Jan 27, 2021

The $14$ -sided polygon can be tiled with $7$ cyan unit rhombi of interior angle $\dfrac{\pi}{7}$ , $7$ blue unit rhombi of interior angle $\dfrac{3\pi}{7}$ and $7$ purple unit rhombi of interior angle $\dfrac{2\pi}{7}$ as follows:

Following the triangle area formula , since

Each cyan rhombus has an area of $2 \cdot \dfrac{1}{2} \cdot 1 \cdot 1 \cdot \sin\dfrac{\pi}{7} = \sin\dfrac{\pi}{7}$
Each blue rhombus has an area of $2 \cdot \dfrac{1}{2} \cdot 1 \cdot 1 \cdot \sin\dfrac{3\pi}{7} = \sin\dfrac{3\pi}{7}$
Each purple rhombus has an area of $2 \cdot \dfrac{1}{2} \cdot 1 \cdot 1 \cdot \sin\dfrac{2\pi}{7} = \sin\dfrac{2\pi}{7}$

The total area is

$7\sin\dfrac{\pi}{7} + 7\sin\dfrac{2\pi}{7} + 7\sin\dfrac{3\pi}{7}$

where $A = B = C = 7$ gives $A + B + C = \boxed{21}$ .

It is known that regular zonogons, like the $14$ -sided regular polygon, can be dissected into rhombi. However, there is not yet a clear (elementary) proof of how many distinct possible numbers of rhombi (of any interior angle) are there for a regular zonogon of $2n$ sides. It's pretty interesting to see that for this problem, the solution is unique.

Here is the next problem I came up with. As my previous problems and this problem caught my attention, I will look more into generalized tilings.

Michael Huang - 4 months, 2 weeks ago

After hours of searching for some interesting articles to read, I encountered that rhombus tilings of a zonogon has more to do with projection. Here is the article for those who are interested. Japanese mathematics is truly elegant filled with magical tricks.

Michael Huang - 4 months, 2 weeks ago

Actually what baffles me about both your solution (and mine) is:

Is there exactly 1 solution to $(A,B,C)$ ? Is there a different tessellation that yields a different $(A,B,C)$ ?

Furthermore, Michael Huang's follow-up problem leds me to think that the answer (to that harder question) is 1 too. But I've found another 2 solutions by running some script. But "3" is not the right answer either. Sigh.

Pi Han Goh - 4 months, 2 weeks ago

That's a beautiful solution. I have a similar question - how do we know it's unique? (I agree that it is, but I wonder if there's a short way of proving it).

@Pi Han Goh - is that the right follow-up problem? It doesn't have 1 or 3 solutions... (or have I misunderstood you? What additional 2 solutions do you mean)?

Chris Lewis - 4 months, 2 weeks ago

The answer is neither 1 nor 3. I cannot get the answer. I'm not spoiling the (numerical) answer here.

What other 2 solutions? I've referring to: "I've found three 7-tuplets of (n1,n2,...,n7) that satisfies his equation in his other question"

Pi Han Goh - 4 months, 2 weeks ago

@Pi Han Goh – Ugh, I've definitely misunderstood, sorry. And don't worry, that's not much of a spoiler!

I was asking about your boxed question (about the uniqueness of $(A,B,C)$ in this problem). It looked like you meant you'd found other tessellations for this $14$ -gon question.

Chris Lewis - 4 months, 2 weeks ago

@Chris Lewis – Oh no need to apologize. My message wasn't clear. (I will edit my comment above)

To be clear, I've found one solution of $(A,B,C)$ to this very problem that we're looking at right now. But I didn't prove its uniqueness.

For Michael Huang's follow-up question , I found 1 solution by myself and found another 2 solutions via a script. But the answer isn't 3 either. So I'm pretty stumped.

Pi Han Goh - 4 months, 2 weeks ago

@Pi Han Goh – Come to think of it, David Vreken's question is much suitable to be phrased as:

Partition a regular 14-gon into quadrilateral such that the following is evident $2\cdot \Bigg [ \sin\left(\dfrac\pi7\right) + \sin \left(\dfrac{2\pi}7\right) + \sin \left(\dfrac{3\pi}7\right) \Bigg ] = \cot \left( \frac\pi{14} \right)$

Pi Han Goh - 4 months, 2 weeks ago

"Is there exactly $1$ solution to $(A,B,C)$ ?" For positive integers $A$ , $B$ , and $C$ , yes. I don't have an elegant proof for it yet, but at least for now here is a quick Python code that checks all the possible positive integer values for $A$ , $B$ , and $C$ , and $A = B = C = 7$ is the only solution:

import math
G = 7.0 * (math.sin(math.pi / 7) + math.sin(2* math.pi / 7) + math.sin(3 * math.pi / 7))
for A in range(1, int(1.0 * G / math.sin(math.pi / 7)) + 1):
    for B in range(1, int(1.0 * G / math.sin(2 * math.pi / 7)) + 1):
        for C in range(1, int(1.0 * G / math.sin(3 * math.pi / 7)) + 1):
            V = A * math.sin(math.pi / 7) + B * math.sin(2* math.pi / 7) + C * math.sin(3 * math.pi / 7)
            if abs(G - V) < 0.0001:
                print(G, V, A, B, C)

David Vreken - 4 months, 2 weeks ago

Replace if abs(G - V) < 0.0001: with if math.isclose(V,G): and it works too.

Pi Han Goh - 4 months, 2 weeks ago

@Pi Han Goh – I didn't know about that function, thanks!

David Vreken - 4 months, 2 weeks ago

@Michael Huang Can you give me some insight on how you found this tiling, I find it quite amusing to think that a fellow human being did this, was it with computer graphics or with pen and paper

Jason Gomez - 4 months, 2 weeks ago

As a unit rhombus consists of all equivalent sides and two pairs of equivalent opposite angles, in a regular unit zonogon of $2n$ sides, the number of possible distinct rhombus choices (including a square, which is a rhombus) to fill in a side of a unit length is as follows:

$\begin{cases} \left\lfloor \dfrac{n}{2} \right\rfloor & \text{for }n\text{ odd}\\ \dfrac{n}{2} & \text{for }n\text{ even} \end{cases}$

where possible interior angles are in the form of $\dfrac{\pi}{n} \leq \dfrac{k\pi }{n} \leq \dfrac{\pi}{2}$ for integers $k = 1, 2, \dots, \left\lfloor \dfrac{n}{2} \right\rfloor$ . The more complex concept involves combinatorial tiling.

Harold Coxeter found that we can tile $21$ parallelograms in a $14$ -sided regular polygon (which came from $\dfrac{7 \cdot 6}{2} = 21$ ). In this case, we see that the shape can be tiled, using $21$ rhombi. The special case that $A = B = C$ more likely follows that $7$ is a prime number. Also consider a regular unit polygon, having $34$ sides. Then, the number of each interior angle of an arithmetic progression between $\dfrac{\pi}{17}$ and $\dfrac{8\pi}{17}$ is $17$ . Thus,

$\dfrac{17}{2} \cot \dfrac{\pi}{34} = 17 \sum\limits_{n=1}^8 \sin \dfrac{n\pi}{17}$

The solution is not unique for $2n$ -gon if $n$ is not prime.

Michael Huang - 4 months, 2 weeks ago

Great solution! For those interested, here are some more other tilings of the tetradecagon (taken from here ) using the same $21$ rhombi as this solution:

David Vreken - 4 months, 2 weeks ago

On the point of uniqueness, firstly this has a very Galois feel. But given I've forgotten all that, assume there is a second solution in integers $(A',B',C')$ , that is $P=A\sin\frac{\pi}{7}+B\sin\frac{2\pi}{7}+C\sin\frac{3\pi}{7}=A'\sin\frac{\pi}{7}+B'\sin\frac{2\pi}{7}+C'\sin\frac{3\pi}{7}$

So $(A-A')\sin\frac{\pi}{7}+(B-B')\sin\frac{2\pi}{7}+(C-C')\sin\frac{3\pi}{7}=0$

ie we can find integers $(X,Y,Z)$ , not all zero, such that $X\sin\frac{\pi}{7}+Y\sin\frac{2\pi}{7}+Z\sin\frac{3\pi}{7}=0$

Multiply by $2\cos\frac{\pi}{14}$ to get $X \left(-\sin\frac{\pi}{14}+\sin\frac{3\pi}{14}\right)+Y \left(-\sin\frac{3\pi}{14}+\sin\frac{5\pi}{14}\right)+Z \left(-\sin\frac{5\pi}{14}+\sin\frac{7\pi}{14}\right)=0$

and rearrange (noting $\sin\frac{7\pi}{14}=1$ ) to $X\sin\frac{\pi}{14} - Z = (X-Y)\sin\frac{3\pi}{14} + (Y-Z)\sin\frac{5\pi}{14}$

Similarly, multiplying by $2\sin\frac{\pi}{14}$ we get $X \cos\frac{\pi}{14} = (X-Y) \cos\frac{3\pi}{14} + (Y-Z) \cos\frac{5\pi}{14}$

Squaring and adding (yes, really), lots of things cancel; we get $X^2-2XZ\sin\frac{\pi}{14} = (X-Y)^2+(Y-Z)^2 + 2(X-Y)(Y-Z)\cos \frac{\pi}{7}$

In other words, $2XZ\sin\frac{\pi}{14} + 2(X-Y)(Y-Z)\cos \frac{\pi}{7}$

is an integer. But $\cos \frac{\pi}{7} = 1-2\sin^2 \frac{\pi}{14}$ , which implies either that

1) $\sin\frac{\pi}{14}$ is the root of a quadratic or linear function with rational coefficients

2) $XZ=(X-Y)(Y-Z)=0$

We know the first of these can't be the case (heptagons aren't constructible with ruler and compass); so $XZ=(X-Y)(Y-Z)=0$

From this, either $X=0$ and $Y=Z$ or $Z=0$ and $X=Y$ . But returning to the equation $X^2-2XZ\sin\frac{\pi}{14} = (X-Y)^2+(Y-Z)^2 + 2(X-Y)(Y-Z)\cos \frac{\pi}{7}$

and substituting either of these gives the unique solution $X=Y=Z=0$ .

So after all that, the representation of any number in the form $A\sin\frac{\pi}{7}+B\sin\frac{2\pi}{7}+C\sin\frac{3\pi}{7}$

with integer $(A,B,C)$ is unique.

Chris Lewis - 4 months, 2 weeks ago

That took way longer than I expected. I had hoped for an amazing magic-trick style reveal, but instead it's more like watching someone find your card by conducting painstaking fingerprint and DNA analysis on the whole deck while you wait.

Shortcuts, anyone?

Chris Lewis - 4 months, 2 weeks ago

Wow, brilliant proof!

David Vreken - 4 months, 2 weeks ago

Chew-Seong Cheong
Jan 28, 2021

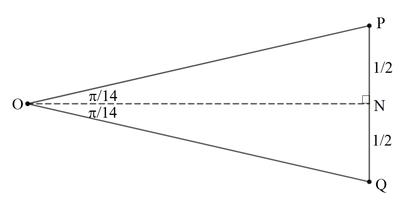
A 14-sided regular unit polygon is made of 14 isosceles triangle with vertex angle measuring $\frac \pi 7$ and base of $1$ . Then the area of the polygon is:

$\begin{aligned} A & = 14 \cdot \frac 12 \cdot PQ \cdot ON = 14 \cdot \frac 12 \cdot \frac 12 \cot \frac \pi{14} \cdot 1 = \frac 72 \blue{\cot \frac \pi{14}} & \small \blue{\text{Note that } \tan \theta = \cot \left(\frac \pi 2 - \theta \right)} \\ & = \frac 72 \blue{\tan \frac {3\pi}7} = \frac 7\blue 2 \cdot \frac {\sin \frac {3\pi}7}{\cos \frac {3\pi}7} & \small \blue{\text{and }\cos \frac \pi 7 + \cos \frac {3\pi}7 + \cos \frac {5\pi}7 = \frac 12} \\ & = 7 \cdot \frac {\sin \frac {3\pi}7}{\cos \frac {3\pi}7} \blue{\left(\cos \frac \pi 7 + \cos \frac {3\pi}7 + \cos \frac {5\pi}7\right)} \\ & = 7 \cdot \frac {\sin \frac {3\pi}7}{\cos \frac {3\pi}7} \blue{\left(\cos \frac \pi 7 + \cos \frac {5\pi}7\right)} + 7 \sin \frac {3\pi}7 & \small \blue{\text{and }\cos(A-B)+\cos(A+B) = 2\cos A \cos B} \\ & = 7 \cdot \frac {\sin \frac {3\pi}7}{\cos \frac {3\pi}7} \cdot \blue{2 \cos \frac {3\pi}7 \cos \frac {2\pi}7} + 7 \sin \frac {3\pi}7 \\ & = 14 \blue{\sin \frac {3\pi}7} \cos \frac {2\pi}7 + 7 \sin \frac {3\pi}7 & \small \blue{\text{and }\sin \theta = \cos \left(\frac \pi 2 - \theta\right)} \\ & = 14 \blue{\cos \frac \pi {14}} \cos \frac {2\pi}7 + 7 \sin \frac {3\pi}7 \\ & = 7 \left(\cos \frac {3\pi}{14} + \cos \frac {5\pi}{14} \right) + 7 \sin \frac {3\pi}7 \\ & = 7 \sin \frac {2\pi}7 + 7 \sin \frac \pi 7 + 7 \sin \frac {3\pi}7 \end{aligned}$

Therefore $A+B+C = 7+7+7 = \boxed{21}$ .

Pi Han Goh
Jan 27, 2021

Disclaimer: I've only found 1 triplet of $(A,B,C)$ , but I didn't prove that this triplet is unique.

The area of a regular $N$ -sided polygon with side length $s$ is given to be $\mathscr A = \frac14 Ns^2 \cot\left (\dfrac\pi N \right).$

In this case, $N = 14, s = 1$ , so $\mathscr A = \dfrac72 \cot \left(\dfrac\pi {14} \right) .$

Through a complete leap of faith, I suspect that $A=B=C$ . This leads me to think about the sum of sines of angles in an arithmetic progression :

$\sum_{k=0}^{n-1} \sin(a + kd) = \dfrac{\sin(n\, d/2)}{\sin(d/2)} \sin \left ( a + \frac {n-1}2 d \right )$

Substitute $a = d = \dfrac\pi7$ , and $n - 1 = 5$ , we have $\begin{array} { r c l } \sin \left(\dfrac\pi7\right) + \sin \left(\dfrac{2\pi}7\right) + \cdots \sin \left(\dfrac{6\pi}7\right) &=& \dfrac{\sin(6\pi/14)}{\sin(\pi/14)} \, \underbrace{ \sin \left(\frac\pi7 + \frac52 \cdot \frac\pi7 \right)}_{=\, 1} \\ \phantom0\\ &=& \dfrac{\cos(\pi/14)}{\sin(\pi/14)} = \cot\left(\dfrac\pi{14} \right) \end{array}$

Using the complementary angle formula, $\sin X = \sin(\pi - X)$ , the left-hand side of the equation above can be expressed as $2\cdot \Bigg [ \sin\left(\dfrac\pi7\right) + \sin \left(\dfrac{2\pi}7\right) + \sin \left(\dfrac{3\pi}7\right) \Bigg ] = \cot \left( \frac\pi{14} \right)$

Multiply both sides by $\frac72$ yields $\frac72 \cot\left(\dfrac\pi{14} \right) = \mathscr A = 7 \sin\left(\dfrac\pi7\right) + 7 \sin \left(\dfrac{2\pi}7\right) + 7 \sin \left(\dfrac{3\pi}7\right)$

Hence, $A=B=C=7\Rightarrow A+B+C=\boxed{21} .$

I think I've got a proof of uniqueness (see under Michael Huang's solution), but it is messy . Perhaps some of the ideas could be used better, though.

Chris Lewis - 4 months, 2 weeks ago

I think that comment deserves to be a solution of its own. I'm still digesting it...

Pi Han Goh - 4 months, 2 weeks ago

Tetradecagon Area

The answer is 21.

3 solutions

0 pending reports