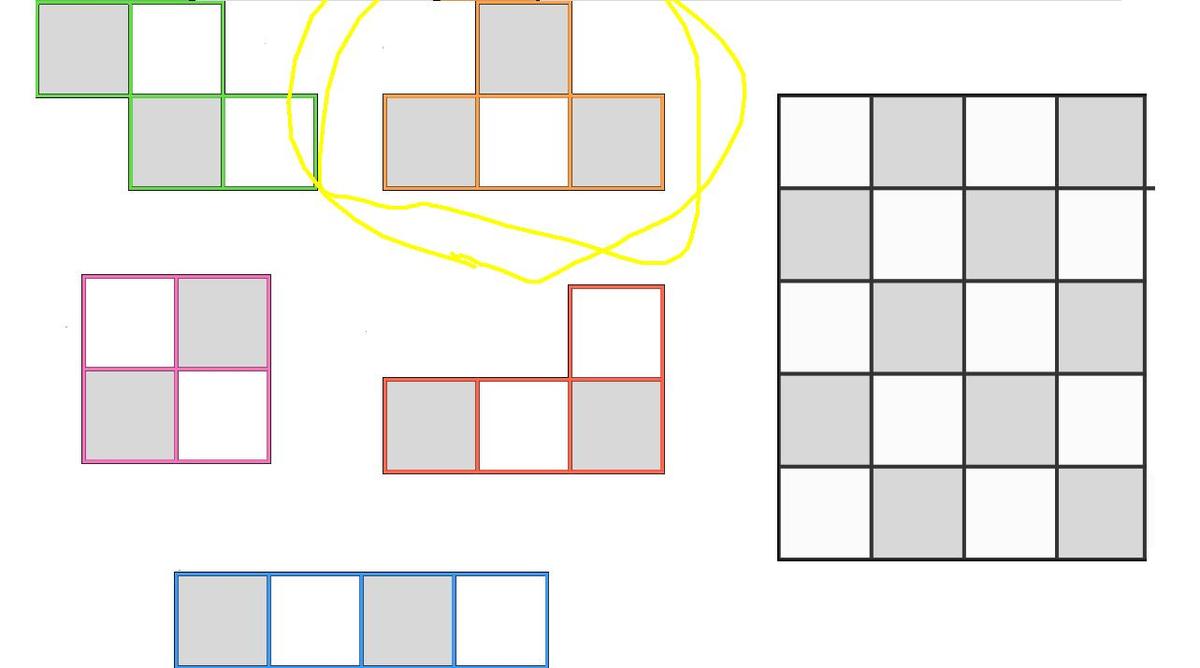
Tetromino Dilemma

Relevant wiki: Coloring (Parity Arguments)

There are $10$ black squares and $10$ white squares on the board. All the shapes except for the orange one covers $2$ black squares and $2$ white squares when placed on the board, regardless of how it is oriented. The orange shape covers $3$ squares of one color and $1$ square of the other color. Adding all the shapes up will result in a different number of black and white squares, which is not how the board is. Therefore, it is impossible to cover the board with these five tetrominoes.

Consider the rectangle colored like a checkerboard. Each tetromino covers exactly two white and two black squares except for the "T" shape which must cover either three white squares & one black square or three black squares & one white square. Since an equal number of black and white squares must be covered to include the complete checkerboard, it is impossible to fit the pieces in a 5 by 4 rectangle.

Relevant wiki: Coloring (Parity Arguments)

The green, purple, red, and blue shapes must cover $2$ white squares and $2$ black squares each when placed on the board, for a total of $8$ black and $8$ white squares. There are now $2$ black and $2$ white squares remaining. However, the orange shape cannot be oriented to cover $2$ black and $2$ white squares. Therefore, it is impossible to cover the board.

In a 5×4 it has 20 square boxes but in the given shapes has only 18 in total

I thought of this like Tetris...

Just look at the shape with a single protruding box. You can intuitively conclude that it is incompatible with the rest of the shapes in filling the whole board just by visual comparison.

Consider the rectangle colored like a checkerboard. Each tetromino covers exactly two white and two black squares except for the "T" shape which must cover either three white squares & one black square or three black squares & one white square. Since an equal number of black and white squares must be covered to include the complete checkerboard, it is impossible to fit the pieces in a 5 by 4 rectangle.

Clearly, there are only six singular pieces or (2 mod 4) anyone you wish so it is not possible to fit this into the rectangle.

Clearly, there are only six singular pieces or (2 mod 4) anyone you wish so it is not possible to fit this into the rectangle

Lets say that its a fraction if you shade in all the parts given to you then it will not fit in all the spaces.

Total count of squares in shapes and total count of squares in the 5X4 box is not same..so the answer is NO

no is the awanser

No need to overcomplicate things. The T shaped piece would leave a gap somewhere on the board. Simply put, if on the bottom, no piece juts down, if on the top, there is no one black piece to fill it, and if in the middle, same problem as with the bottom. Also, even taking into account rotation, there would still end up a gap.

The checkerboard has equal number of black and white sqares All shapes except the Orange when placed would cover an equal number of black and white squares...

But the Orange Shape however placed will cover 2 extra squares of some colour...but the board has an equal number of black and white squares that are to be covered.

Therefore it is not possible to cover it using 1 of each of the coloured shapes given.

The box contains 20 individual smaller boxes. The pieces in the solution contains 21 small individual boxes collectively. There is no way to fit 21 boxes into a space that only contains 20 boxes. The answer is "no"

The trick seems to be to imagine the checkerboard in the tile and not trying to place them on the board in your mind.

My intuition was something like "There too many tiles art facing upwards...creating holes in the mosaic...not depending on how you'd combine them."

Maybe it's about not being able to create a 5x4 rectangle out of the tetris tiles.

There needs to be a certain kind of symmetry, which is probably easiest done dividing the piles into black and white subpieces.

Anyway, I could also use a scissor to divide the ones that aren't fitting - or change the checkerboard...or the rules of the question.

If there doesn't seem to be a solution you haven't thought about the problem enough yet, imo. ;)

Also, I thought that a checkerboard is defined as a 8x8 board? And it's not a square...