Harmonic At It's Best
Let
A = 1 0 0 1 1 + 1 0 0 2 1 + 1 0 0 3 1 + ⋯ + 3 0 0 1 1 .
Then x < A < 3 y .
Where x is the greatest integer possible in its range and y is the smallest integer possible in its range.
Find the value of x + y .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
There is a typo.
It should be ln ( 1 0 0 1 3 0 0 1 ) not ln ( 1 0 0 0 1 3 0 0 1 )
Log in to reply
Thank you for pointing out the typo. I don't have a link or anything, but I think I can make it more clear if I draw a picture. Give me some time I will add a picture to the solution.
Could you explain this continuous approximation of x 1 ?
Could you give me a link?
Log in to reply
Ok, I've added the picture. If you have any more questions after studying the picture, I will try to answer them.
Also, making the picture made me realize my first edit was slightly off! I corrected the limits and now the restriction on A is even better ! :)
Log in to reply
Thanks for the explanation
how did you get the picture
Log in to reply
@Rajdeep Dhingra – I drew the picture on my computer... Do you mean how did I think of it?
I thought of it because a series, (like Σ n 1 ), is just an approximation of the area of the continuous case, (like ∫ x 1 d x ). Instead of d x , you have Δ x = 1 .
But there are two ways to approximate an integral; by too much (rectangles above) or by too little (rectangles below). I just used this idea to constrain the sum.
This idea (of approximating integrals with Δ x instead of d x ) is pretty fundamental to calculus. Calculus is built out of the limit of Δ x → d x
To be honest, I don't know any 13 year olds who know calculus, but if you're on this website, you must be pretty smart :)
Log in to reply
@Nathanael Case – No I meant how did you drew the image on your computer?
Using which software?
Log in to reply
@Rajdeep Dhingra – I have a mac, so I used something called "Paintbrush"
Side note: If we average the two limits:
2 1 ln ( 1 0 0 1 3 0 0 2 ) + 2 1 ln ( 1 0 0 0 3 0 0 1 )
we get a very good approximation of the sum (correct to 6 decimal places)
From a question I encountered yesterday, the value of the nth harmonic number is the same as y + l n ( n ) , where y is the constant, which by manipulating gives us 2 y + l n ( 3 0 0 1 ) − l n ( 1 0 0 0 ) − 1 = 1 . 2 5 3 3 Is this still a good approximation? I'm talking about when the value of this becomes 0 . 9 9 while the true value is 1 . 0 1 which gives different answers for the question.
Log in to reply
Actually, because H n ∼ γ + ln n (that's a gamma, by the way), what you get is A ≈ ln 3 . 0 0 1 . You made a mistake somewhere in the algebraic manipulation. We can then use our intuition to bound A .
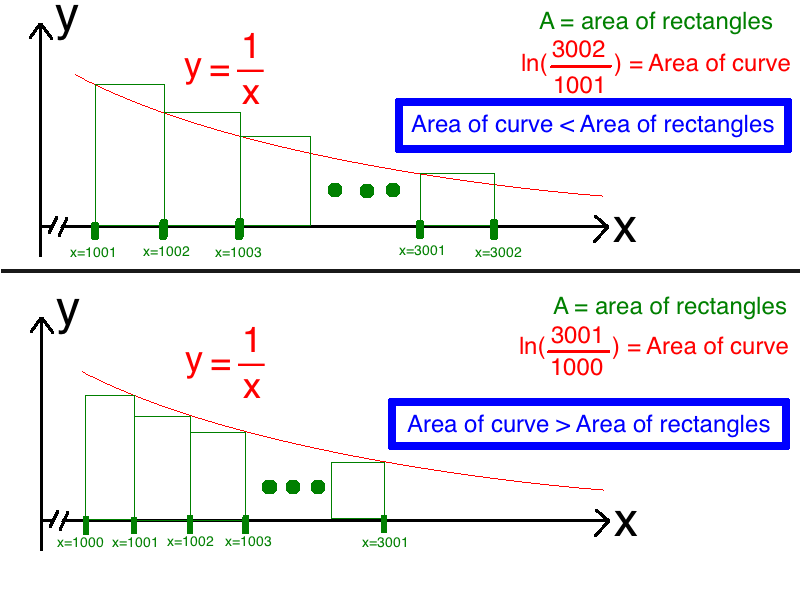
I used the continuous form 1/x to find a lower bound and upper bound for A
So if we call the sum "A" like in the problem then we have:
1 0 0 1 ∫ 3 0 0 2 x d x < A < 1 0 0 0 ∫ 3 0 0 1 x d x
ln ( 1 0 0 1 3 0 0 2 ) < A < ln ( 1 0 0 0 3 0 0 1 )
1 . 0 9 8 3 < A < 1 . 0 9 8 9
That puts a pretty good restriction on A! Therefore 1 < A < 3 4
Here is a picture to explain the idea: