Chomp the Row & Column!
Note: This was a contest question hosted earlier by me, so don't get confused by the comments of the solutions posted in this problem.
Today's question is based on the game of Chomp, you can check its rules and more about it here: Chomp
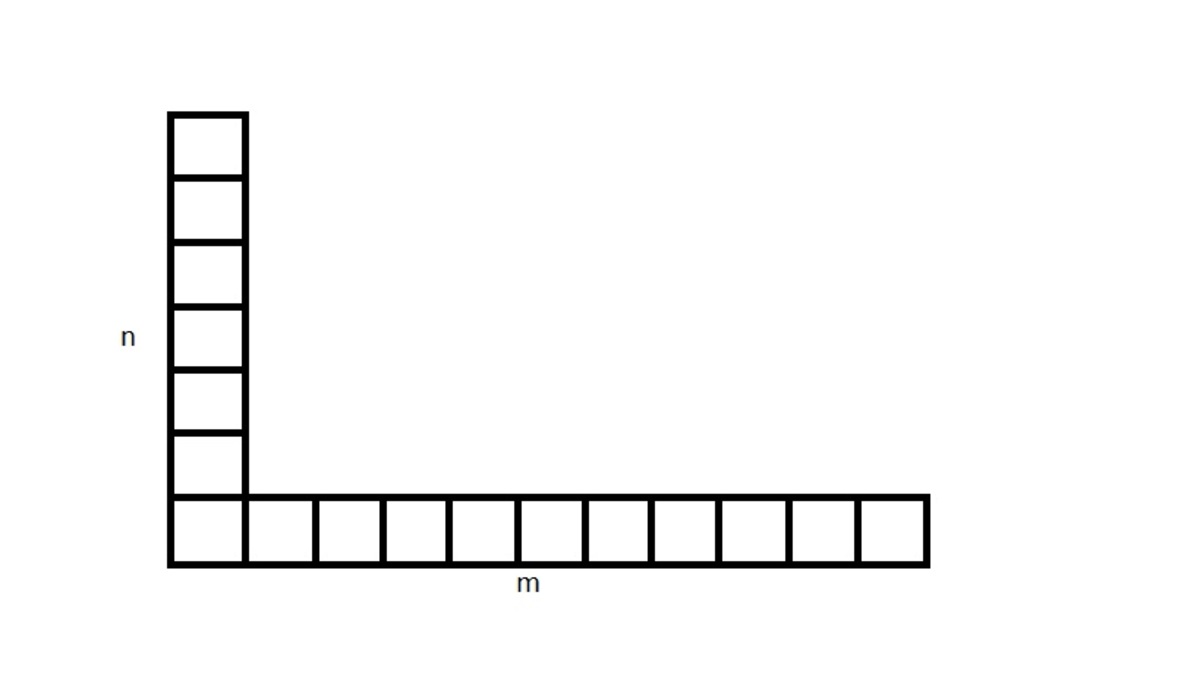
Question: Suppose Sierra and Caleb are playing Chomp, its Sierra's turn and she is left with the arrangement as shown below where there are m rows to the right and n squares up, and m > n . Is there any strategy for Sierra that guarantees her winning, assuming optimal play from both the players. It is not a rectangular piece below, it is an arrangement with a row of m squares and a column of n squares.
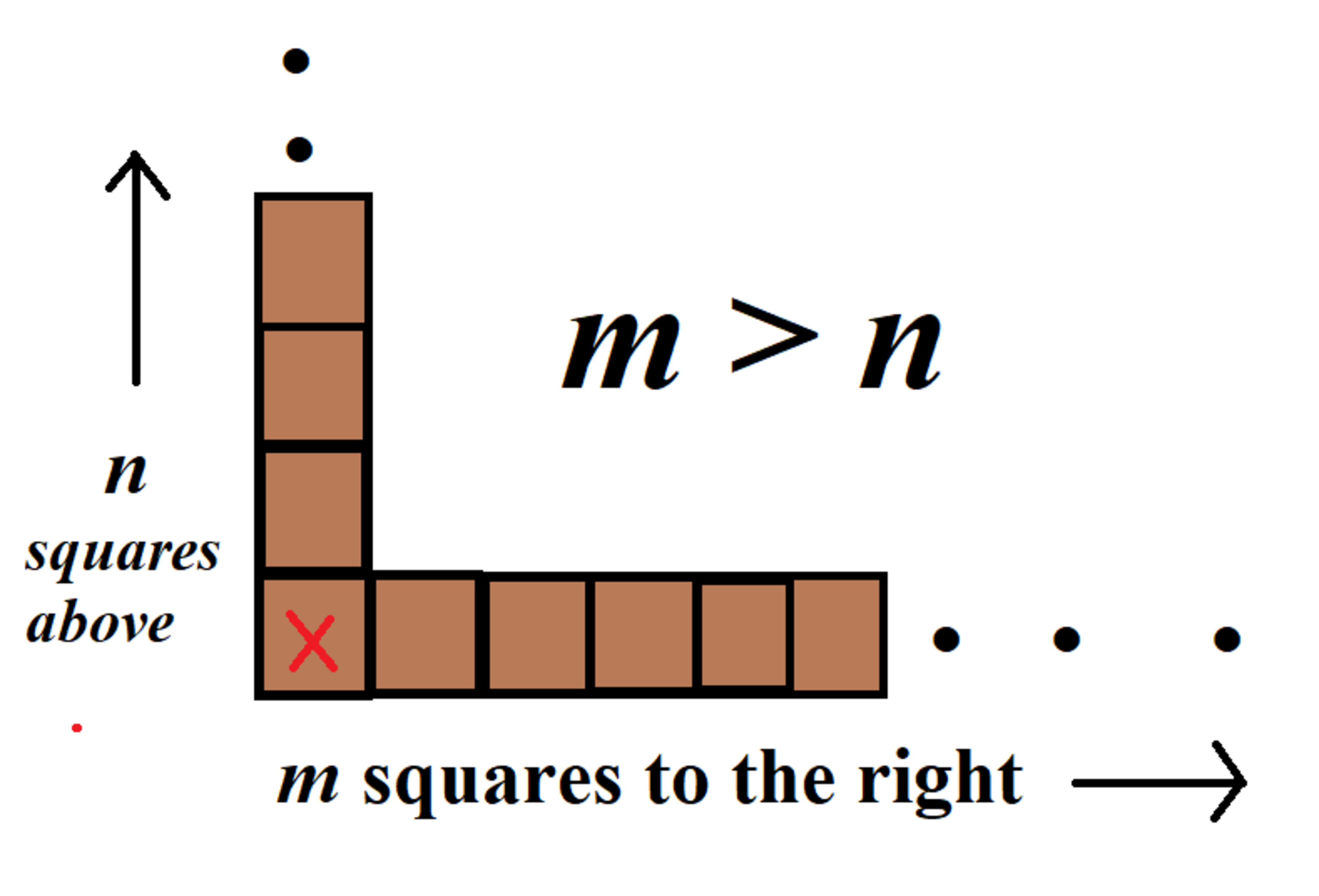 The arrrangement
The arrrangement
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
11 solutions
Before giving any points, see that if you have something to edit, that is if you have used enough latex or pictures, or the link to Nim-sum's proof or something else. Then mention me to give points when you want.
@Siddharth Chakravarty I'm done with links of Game of Nim and XOR operator , and the photos . You could give scores now.
Proof by induction
It is not possible for m = n Actually, it is stated that m > n . from beginning, so Sierra can eat that many pieces in her first move, so that for Caleb’s first move, m = n , then this procedure follows.
So, no matter what, there is a strategy for Sierra, since she is the first player.
@Siddharth Chakravarty , I need a clarification, do you mean there is a rectangle chocolate or there is just chocolate as shown in the picture?
Log in to reply
It is not a rectangular piece, as I have not shown a complete rectangular piece. I have also added a statement for it so that there is no more confusion. Also, present any strategy what Sierra will use, I am giving you the last chance to edit and then I will give you points.
Log in to reply
Ok, then I'll probably change my solution a little, maybe not, but please don't give me points until I ask you. Thanks!
@Siddharth Chakravarty , now I have edited. Thanks for giving me time!
Sierra has a killer strategy to win
Since Sierra is moving first, she must try to make the bar symmetric like this -
Once she eats m − n squares from the leg with m squares, both legs will have n number of squares and the bar will be symmetric like this -
Then the winning strategy for Sierra becomes simple - She just has to copy Caleb. Copying Caleb will make the bar retain its symmetry like this -
Caleb eats Y squares, and Sierra copies him. This will continue until Caleb eats a square next to the X square. When Caleb eats a square that is next to the X square, Sierra can copy him like this -
L e a v i n g t h e X s q u a r e f o r C a l e b .
( This is all true, assuming they are both at optimal play, as it was mentioned in the question )
Chomp Game Explained - I learnt about Chomp today from this place, so you can too!
I will say stop being Percy Jackson for this contest at least 😂 Just mention me when you want me to give you points.
Log in to reply
Sure, I'll mention you at the right time. OK I'll ask Frank to write it for me (he isn't dyslexic).........
Sierra's Strategy
On her first turn, Sierra should eat m − n squares on the m leg so that it becomes the same length as the n leg:
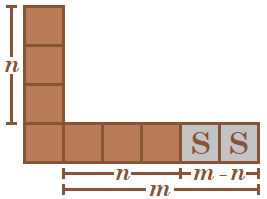
Then for all her turns after that, if Caleb eats x k squares of one leg on his k th turn, then Sierra should eat x k squares of the other leg on her ( k + 1 ) th turn:
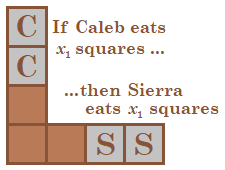
Example
Here is one example of a game where Sierra uses her winning strategy:
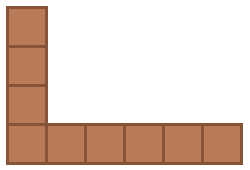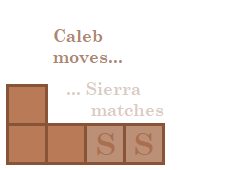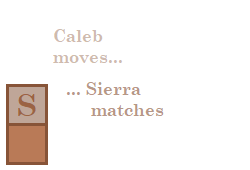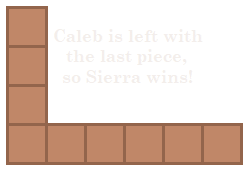
Analysis
By eating m − n squares on her first turn, Sierra makes both chocolate legs have the same length of n . Then by matching Caleb's squares for all her turns after that, Sierra can keep both chocolate legs the same length of
n − k = 1 ∑ t x k
(after Caleb has had a total of t turns). By keeping both chocolate legs the same length, Sierra is guaranteed that there will always be x k matching squares for her to eat that will not include the lower left square.
In other words, no matter what Caleb does, Sierra can counter, so eventually Caleb will be left with the last square, making Sierra the winner!
Weird coincidence: I have a son and daughter named Caleb and Sierra.
Log in to reply
Really, I didn't know that. Maybe I need to put a disclaimer, that this is purely coincidental if any resemblance is found LOL. Should I give you points? Like, don't you want to use more Latex? or any pictures?
Log in to reply
Doesn't the animation count as a picture as well?
Log in to reply
@David Vreken – It is a sequence of pictures, but no they are counted separately here.
Log in to reply
@Siddharth Chakravarty – I'll do some more editing then if that's allowed.
Log in to reply
@David Vreken – Yes, that is, just mention me when you want me to give scores.
Log in to reply
@Siddharth Chakravarty – Okay, I'm finished editing. Thanks!
| Criteria | Points | Reason |
| Intelligble Solution | 15 | The solution is clear and well-explained with a smooth animation. |
| Uniqueness | 0 | The strategy is the same. |
| Using L A T E X | 4 | L A T E X could be used more for formatting, I am giving this for using all the symbols in Latex and little formatiing. |
| Animation | 7 | Animation is used |
| Pictures | 7 | Pictures are used |
| Total Points | 33 |
Log in to reply
Thanks! And thank you for your time on heading up this competition!
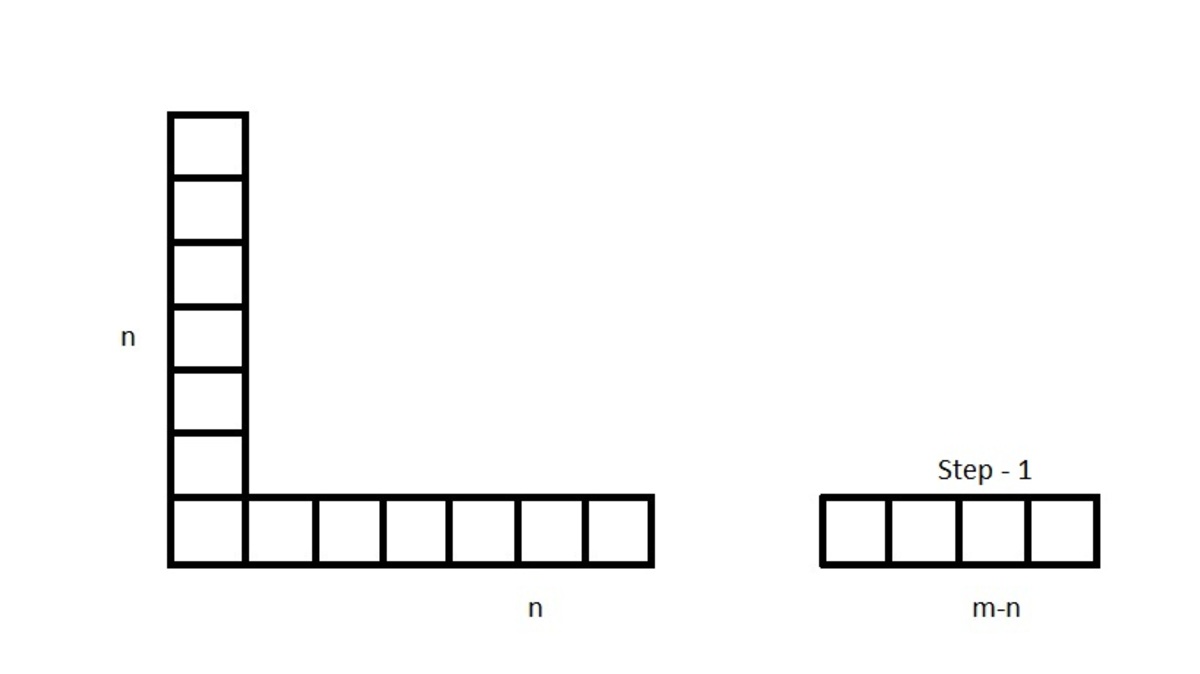
We've a column of n squares and a row of m squares and m>n
Step - 1
Sierra chops off
m
−
n
squares from the row so we have same numbers of square in row and column.
Step - 2 & 3
Now, let x be the no. of squares Caleb takes away,so Sierra will also chop off same amount
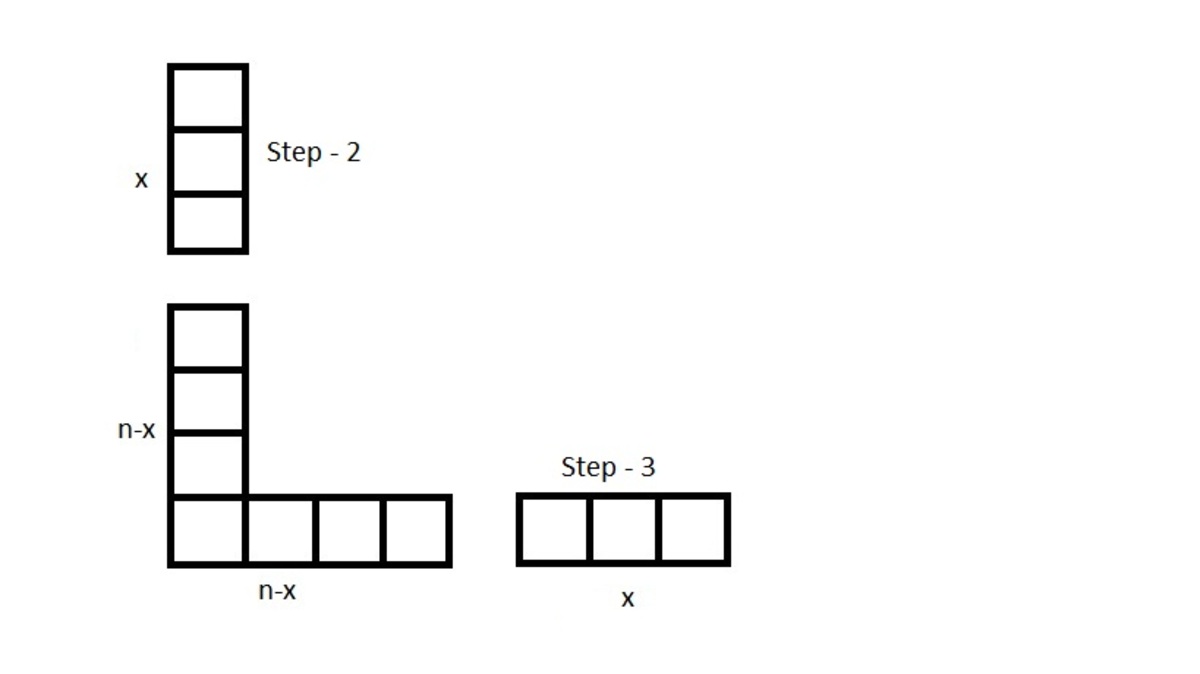
Step - 4 & 5
Repeating steps 2 & 3 till the last square remaining, Sierra
(Player-1)
will always be the winner.
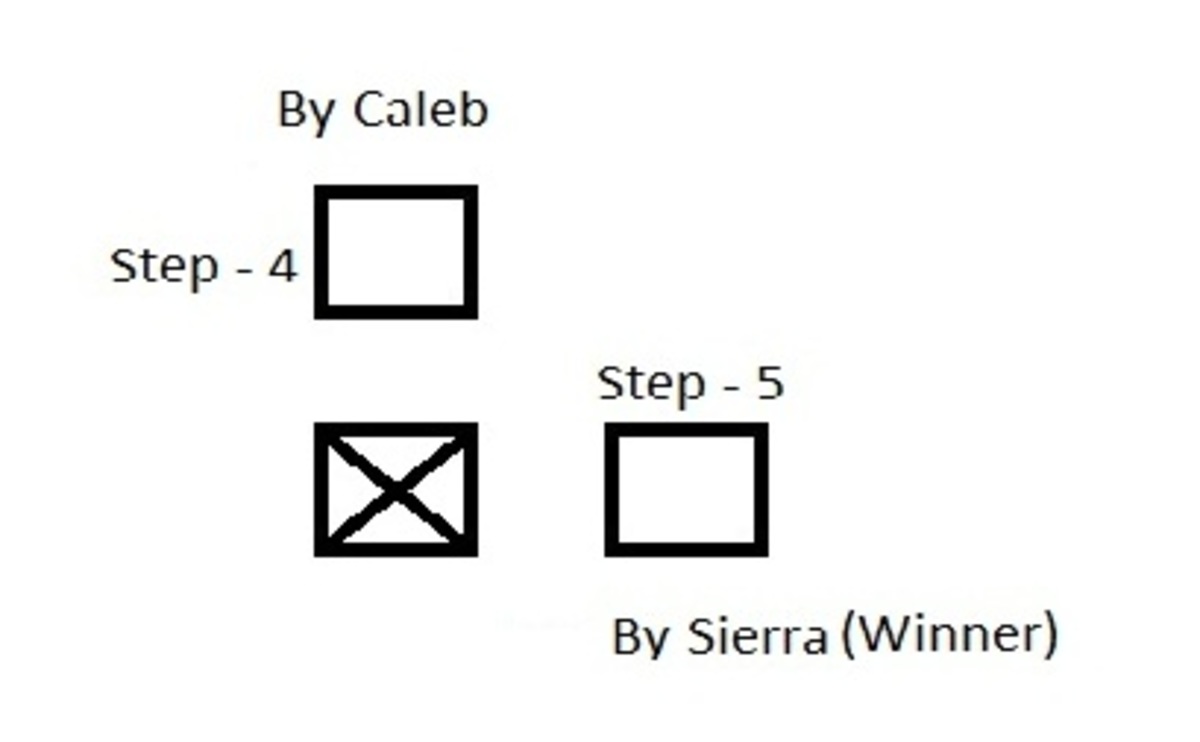
By this Startegy, Players 1 will always win.
However, if we start with m=n, then Caleb is advantageous cause he becomes the Pseudo-Player-1
@Siddharth Chakravarty , you can score my solution.
| Criteria | Points | Reason |
| Intelligble Solution | 15 | The solution is easy-to-understand and correct. |
| Uniqueness | 0 | This is a very common approach |
| Using L A T E X | 0 | Barely any L A T E X is used, for which so next time please use a bit more L a T e X for headings, symbols and as you like! |
| Animation | 0 | No Animation is used |
| Pictures | 7 | Pictures are used |
| Total points | 22 |
This is equivalent to a game of
Nim
. Think of the straight column(except for the bottom-left corner) as stack 1, and the horizontal one(also except for the bottom-left) as stack 2.
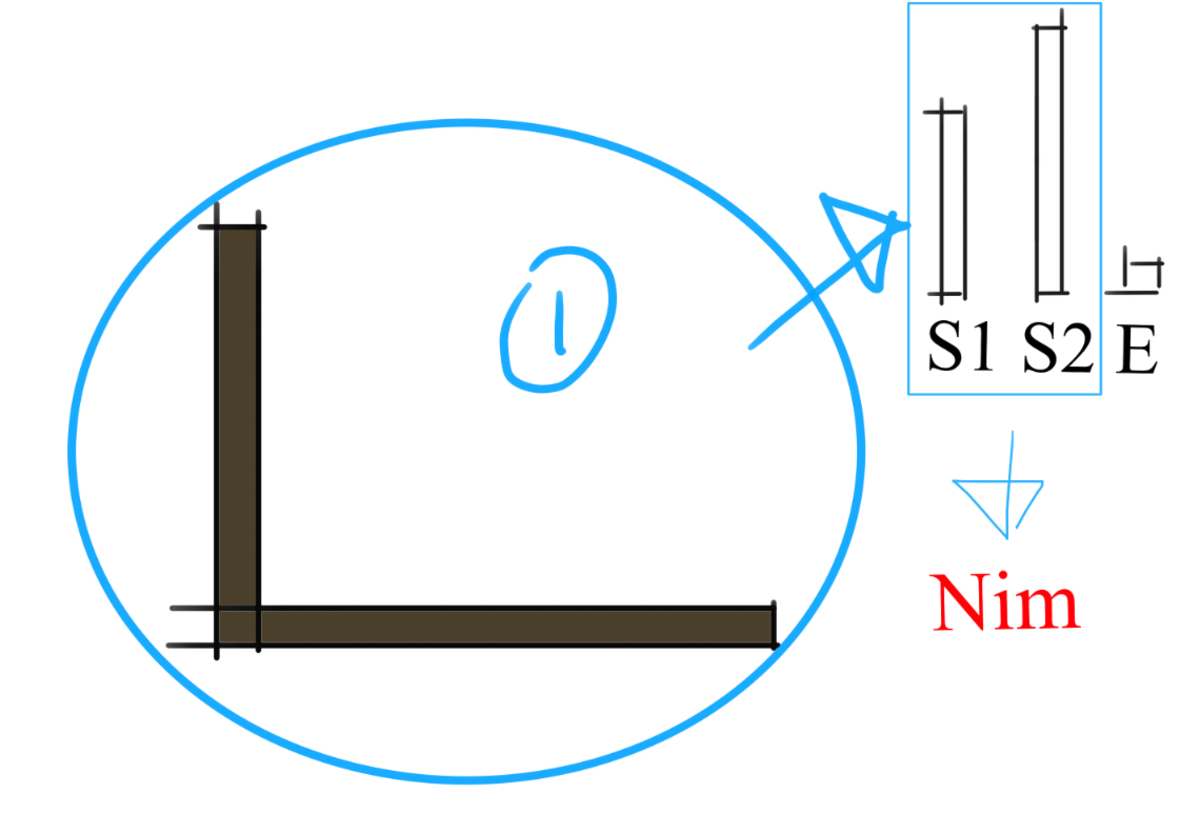 Now winning is equal to making the last move.
Now winning is equal to making the last move.
First, we note that
m
⊕
n
=
0
where
⊕
stands for XOR or there is no optimal strategy.
Since Sierra moves first, she can reduce the number of elements in stack 1 so it is congruent to stack 2 by taking
(
m
−
n
)
elements.
Then all we have to prove is that as long as Caleb can make a move, so can Sierra. This is simple—if Caleb takes elements
a
,
b
.
.
.
n
from stack 1, Sierra can do the same to stack 2 since they are congruent, which keeps the congruency.
This works
vice versa
and we see that Sierra has an optimal strategy to win as in Nim.
Done,
@Siddharth Chakravarty
Should I give you points now?
| Criteria | Points | Reason |
| Intelligble Solution | 15 | You have written in a very short way, and it is a clear explanation |
| Uniqueness | 0 | Although, you used comparison to Nim but the strategy is the same |
| Using L A T E X | 0 | Barely L A T E X is used, use it next time to format text in a clear way, use more symbols and as you like |
| Animation | 0 | Animation is not used |
| Pictures | 0 | Picture is used |
| Total points | 22 |
m>n , first movement is eat m-n squares , so the result is m=n , so on until result is m=n=1 and win.
It is ready @Siddharth Chakravarty
| Criteria | Points | Reason |
| Intelligble Solution | 7 | The solution is correct, but please write in clear way. |
| Uniqueness | 0 | The strategy is the same. |
| Using L A T E X | 0 | L A T E X is not used |
| Animation | 0 | No Animation is used |
| Pictures | 0 | No Pictures are used |
| Total Points | 7 |
Log in to reply
LOL, this guy has 0 enthusiasm for this awesome contest @jordi curto , @Siddharth Chakravarty
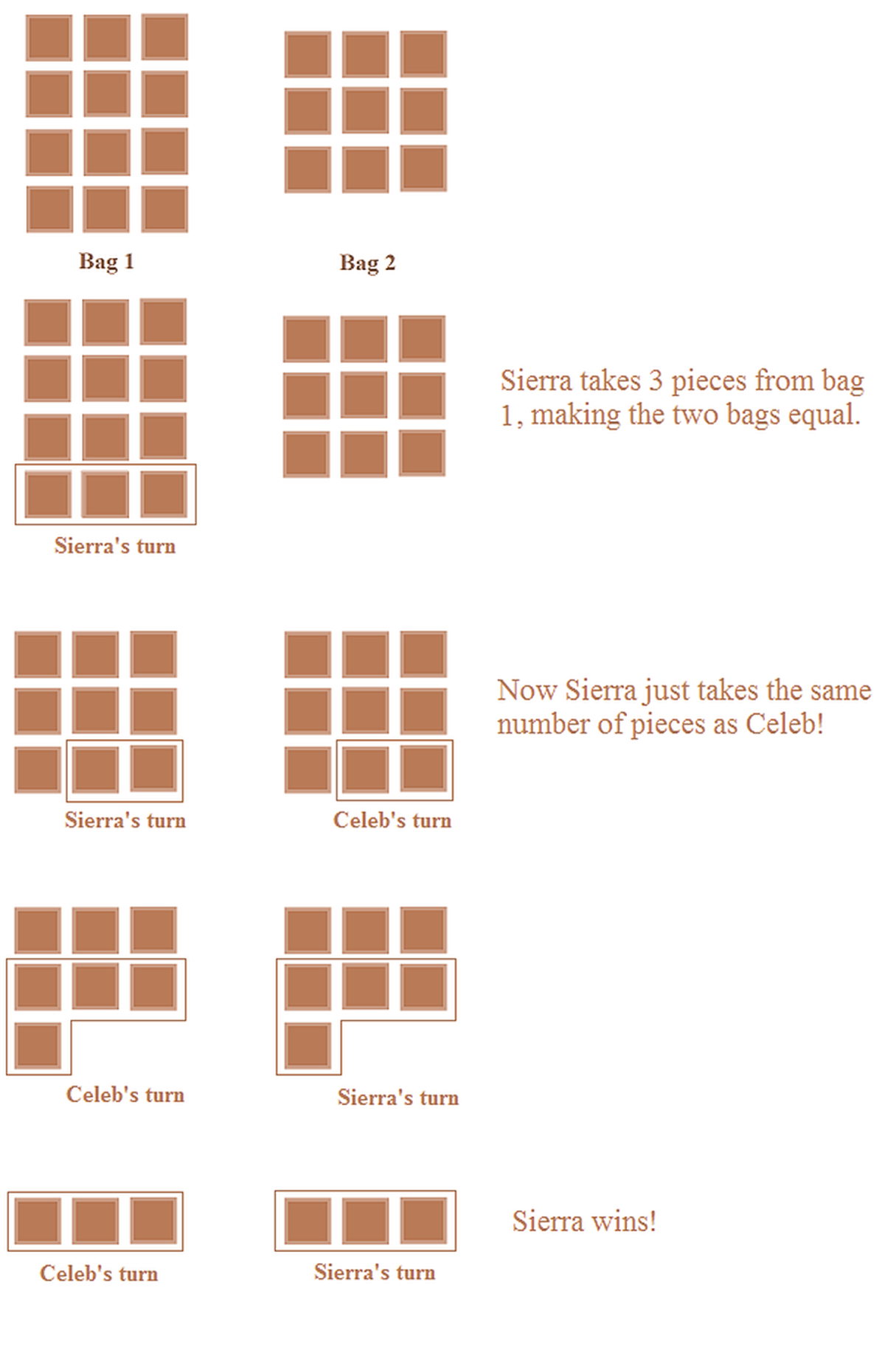
This problem can be simplified as a Nim game :
Sierra and Celeb has two bags with m and n chocolate pieces respectively ( m > n ) . Each of them take turns picking a bag and taking some chocolate pieces from that bag. The person who takes the last piece will win. It's Sierra's turn. Assuming both of them play optimally, is there any strategy for one to win?
In the case of two bags, there's a really easy strategy for Sierra to win:
- First, take m − n chocolate pieces from the bigger bag, leaving the two bags with equal pieces.
- If Celeb takes a pieces from a bag, simply take a pieces from the other bag.
So Sierra have a strategy to win the game.
The picture below shows an example of the game.
Before mentioning me to give scores, see if you want to add more Latex, pictures or any animation. I feel this is very little Latex. I will give you scores after a few hours even if you mention because its late night and I need to go to sleep.
Log in to reply
@Siddharth Chakravarty That's indeed very little Latex, because I really don't know what to write. This is a really easy logic problem, so you can't expect much Latex, picture or animation ... And uniqueness is also nearly impossible here. So on the next days please post some harder problem, then more special things can come to play :).
I'm ready for scoring.
| Criteria | Points | Reason |
| Intelligble Solution | 15 | The solution is clear and well-explained. |
| Uniqueness | 0 | The strategy is the same. |
| Using L A T E X | 0 | L A T E X could be used more for formatting, but this is very little. Use a little more next time. |
| Animation | 0 | Animation is not used |
| Pictures | 7 | Picture is used |
| Total Points | 22 |
The strategy
Sierra = ALICE and Caleb = BOB .
ALICE makes the first move, as shown in the figure:
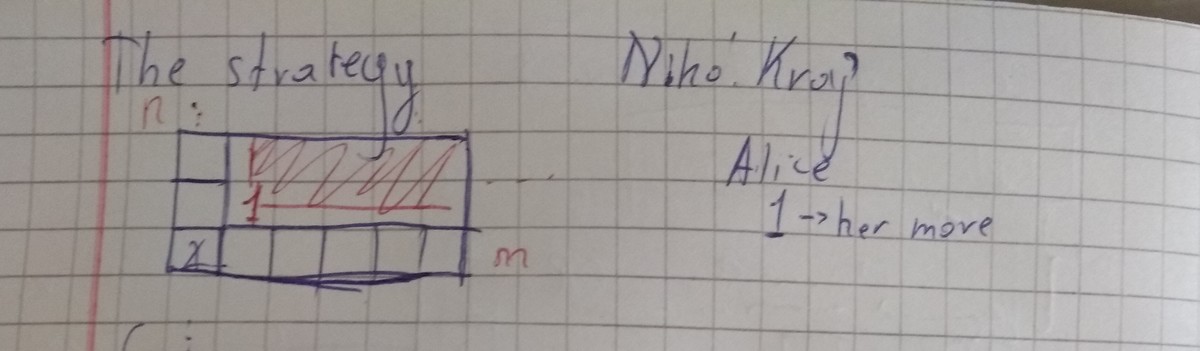
 After
ALICE
s move,
After
ALICE
s move,
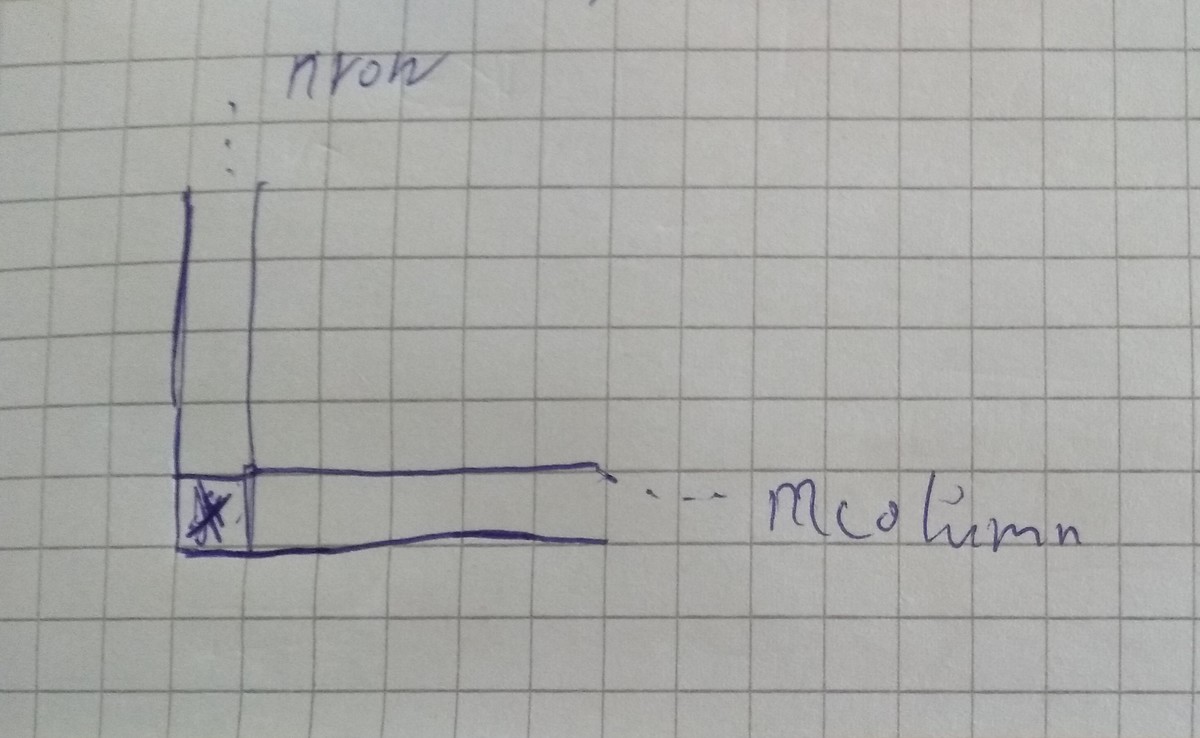
BOB has now 6 possible moves (from the way I see fit):
 Case 1
Case 1
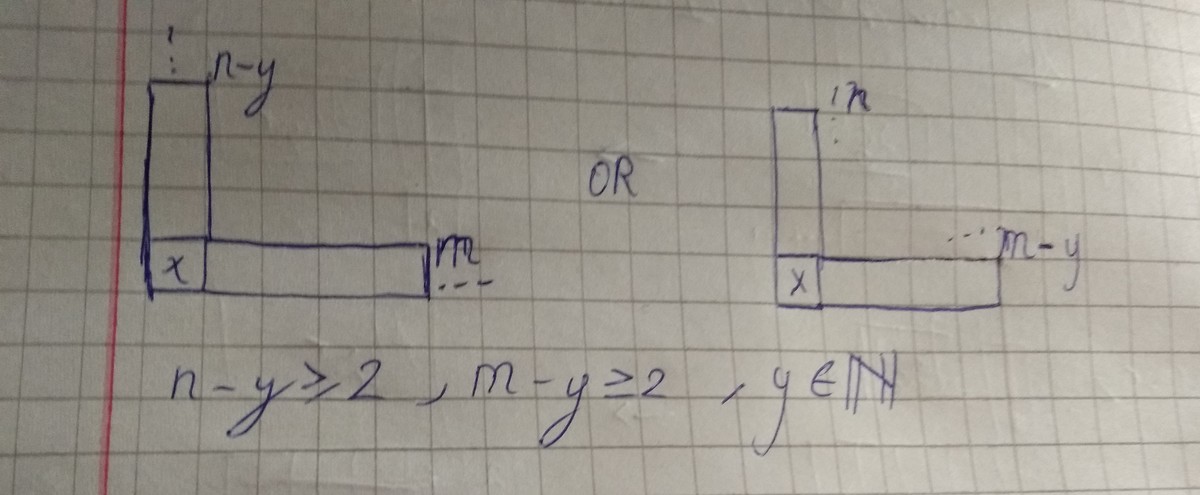 Case 2
Case 2
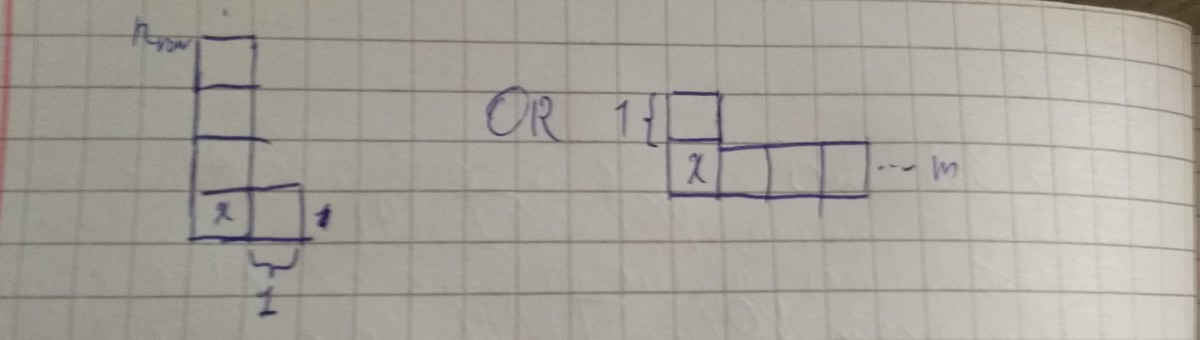 Case 3
Case 3
Take the entire m column, O R to take n row (except the x ) (case 1),
Take almost all the m column O R n row, leaving one box free (except the x ) (case 2),
Take almost all the m column O R n row, leaving two or more boxes free (except the x ) (case 3),
If none of these options work, we have a guarantee that ALICE wins if she plays optimally.
Try these on paper!
Case 1
- If BOB takes all the n row, ALICE counteracts of taking all m column. NOT FAVORABLE MOVE!
- If BOB takes all the m column, ALICE counteracts of taking all n row. NOT FAVORABLE MOVE!
Case 2
- If BOB takes almost all the m column leaving one box free, ALICE counteracts by doing the same to the n row (taking all the boxes leaving one free). BOB is forced to take one of either free boxes . ALICE takes the other free box. NOT FAVORABLE MOVE!
- If BOB takes almost all the n row leaving one box free, ALICE counteracts by doing the same to the m column (taking all the boxes leaving one free). BOB is forced to take one of either free boxes. ALICE takes the other free box. NOT FAVORABLE MOVE!
Case 3
- If BOB takes almost all the m column leaving two or more boxes free, ALICE counteracts by taking almost all the m column leaving one box free. By the figure:
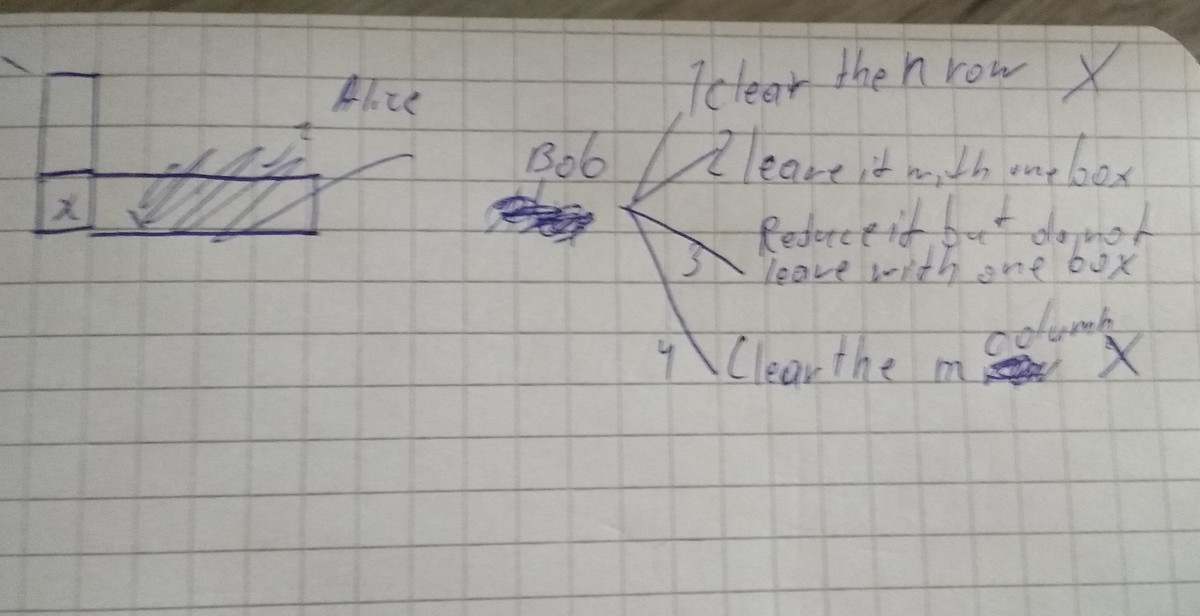
1 and 4 clearly lead to failure. 3 In this case ALICE will take almost all that's left of the n row leaving one box free. BOB is forced to take one of either free boxes . ALICE takes the other free box. 2 In this case ALICE will take almost all on the m row leaving one box free. BOB is forced to take one of either free boxes . ALICE takes the other free box.
Since all these cases of Case 3 lead to failure for poor BOB NOT FAVORABLE MOVE!
Result:
Take the entire m column, O R to take n row (except the x ) (case 1), NOT FAVORABLE MOVE!
Take almost all the m column O R n row, leaving one box free (except the x ) (case 2), NOT FAVORABLE MOVE!
Take almost all the m column O R n row, leaving two or more boxes free (except the x ) (case 3), NOT FAVORABLE MOVE!
If none of these options work, we have a guarantee that ALICE wins if she plays optimally.
This took a LOT to make! Please upvote!
One thing, I would say that you misinterpret the question, it is not a rectangular piece it is an arrangement which only a row with m squares and column with n squares. Also. here BOB can defeat ALICE by taking m-n squares in the row and continue on the procedure to match the no. of squares in the row and column so that Sierra loses. I feel sad that you wrote so much, I give you the last chance to write and edit again as this is the first Q. Don't delete the solution otherwise you won't be able to write again, just edit it.
The game is a finite, impartial, combinatorial game. For such games every game state is either "winnable" (the first player has some winning strategy) or "unwinnable" (the second player has some winning strategy). In this setting, we can prove by induction that each "symmetric" state is "unwinnable", while all other states are "winnable".
- Theorem: all "symmetric" states (having the bottom left square with m squares to the right and m squares up) are unwinnable.
When m = 1 , there are three possible first moves for the first player (Sierra) -- eat the top square, the right most square, or the whole thing.
- If Sierra chooses to eat the top square, the second player (Caleb) can eat the right most square and win.
- If Sierra chooses to eat the right most square, Caleb can eat the top square and win.
- If Sierra chooses to eat the whole thing, Caleb wins straight away.
Therefore, this game state is "unwinnable", and the statement holds true when m = 1 .
Suppose the statement holds true for any m < k , now let's examine the game state of having the bottom left square with k squares to the right and k squares up.
there are 2 k + 1 possible moves for Sierra -- eat the top x squares, the right most x squares, or the whole thing. ( x = 1 , 2 , … , k )
- If Sierra chooses to eat the top x squares, the Caleb can eat the right most x squares and the state becomes "unwinnable", as now m = k − x < k .
- If Sierra chooses to eat the right most x squares, Caleb can eat the top x squares and the state becomes "unwinnable", as now m = k − x < k .
- If Sierra chooses to eat the whole thing, Caleb wins straight away.
Therefore, this game state is "unwinnable", and the statement holds true again. By induction, the theorem is proved.
Now that we know that all "symmetric" game states are "unwinnable", we can easily show that all other game states are "winnable". This is because the Sierra can simply eat the difference off of the longer side and make the game state "symmetric" in one move.
The winning strategy for Sierra is indeed to eat the difference off of the longer side and make the game state "symmetric" every single move. Note that this strategy is unique, because if Sierra strays away from this in any move, the game state will no longer be "symmetric", therefore "unwinnable" for Caleb. Caleb can now use the strategy instead and be guaranteed to win.
Should I give you points? Please mention me next time you want me to give points.
@Siddharth Chakravarty Sorry I forgot it. Please give me scores and thank you for letting me know.
| Criteria | Points | Reason |
| Intelligble Solution | 15 | The explanation is clear the proving is ingenious. |
| Uniqueness | 0 | This strategy is the same |
| Using L A T E X | 4 | Little L A T E X is used for bolding and in a lot of symbols |
| Animation | 0 | No Animation is used |
| Pictures | 0 | No pictures are used |
| Total points | 19 |
How to find a suitable stragegy for Sierra:
Let's start by considering a simple case:
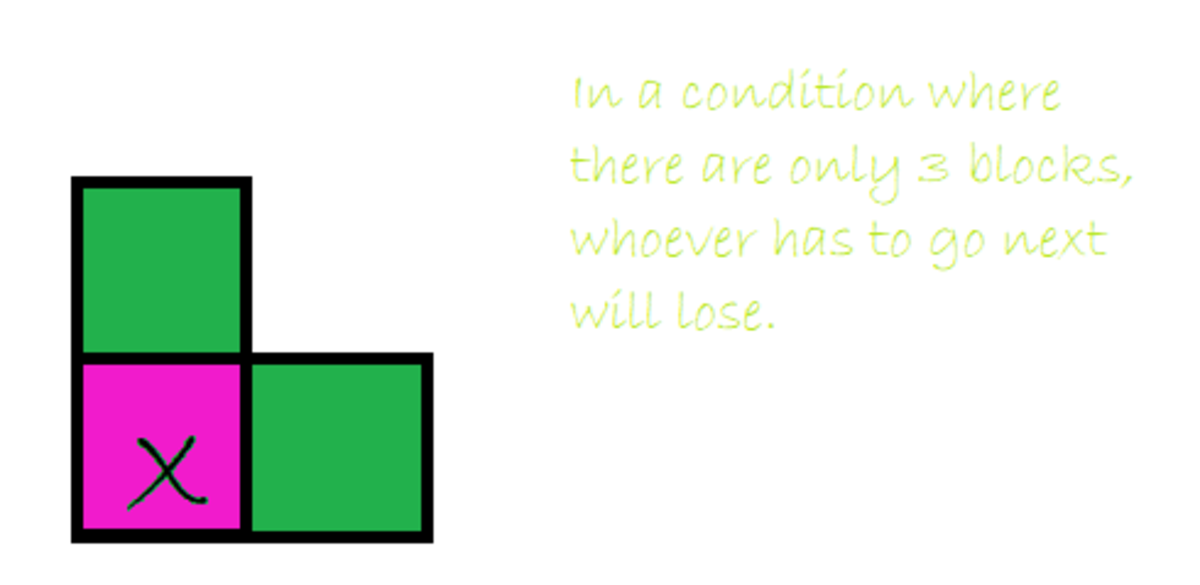
Player 1 must remove one of the green squares. Player 2 can then remove the other block, securing a win.
We can generalize this case stating that if Sierra can make an equal number of blocks above and to the right (i.e. - m=n), she can win.
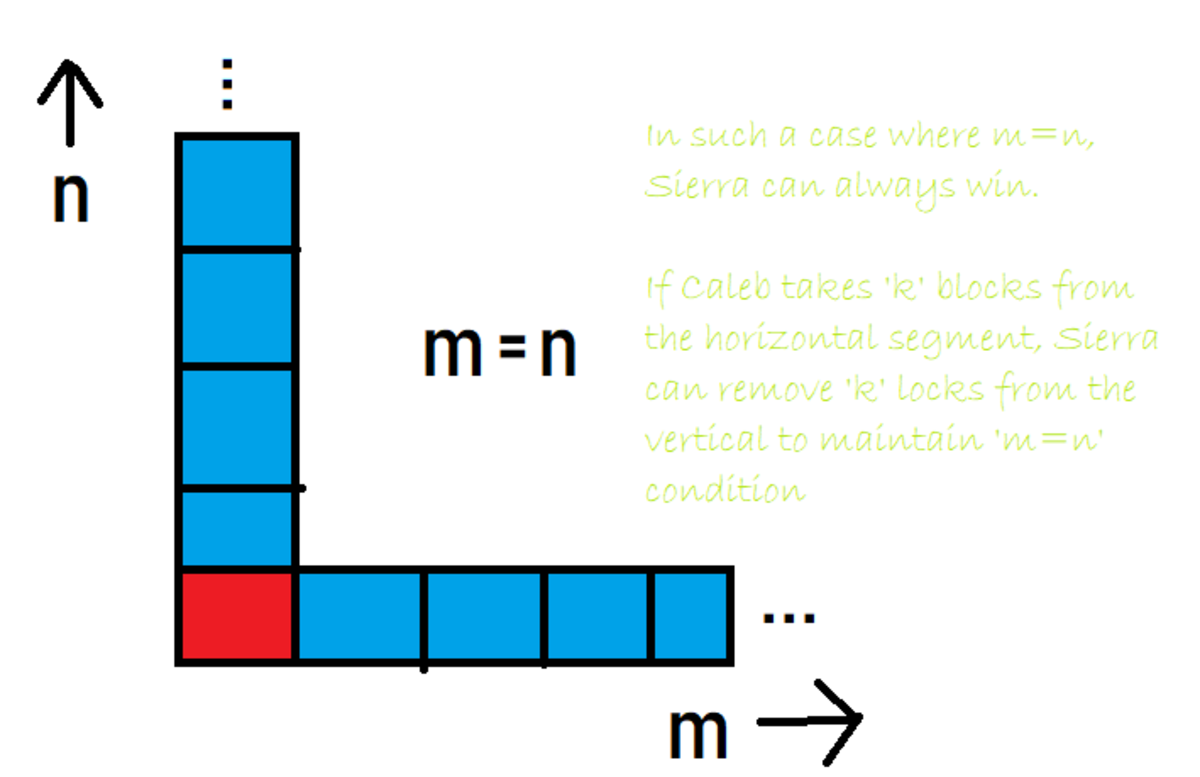
To win, Sierra has to maintain a condition where there are an equal number of blocks to the right and upwards until they reach the base case, with three blocks remaining, and Caleb to play.
Hence:
By taking ( m − n ) blocks out of the horizontal row, Sierra can always win.
I'm still editing @Siddharth Chakravarty . I'll post here when I finish.
Log in to reply
@Siddharth Chakravarty - I'm ready. You can score my solution.
| Criteria | Points | Reason |
| Intelligble Solution | 15 | The explanation is correct and clear, but next time try to write in a easy way as it looks a bit misinterpreting at the first view. |
| Uniqueness | 0 | This is a very common approach |
| Using L A T E X | 0 | Barely any L A T E X is used, next time try to bold your heading and use more Latex type symbols. |
| Animation | 0 | No Animation is used |
| Pictures | 7 | Pictures are used, but write your text in a dark and clear color! |
| Total points | 22 |
Log in to reply
I'll try another colour for sure. It seemed clear on my device, but I'll change.
Game Of Nim