Think about 5
( x + 3 ) ( x + 4 ) ( x + 6 ) ( x + 7 ) = 1 1 2 0
Find the sum of all reals x satisfying the equation above.
The answer is -10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
23 solutions
This one's a lot simpler than the first one....
Log in to reply
First one is Just more work, but the 2nd one needs the insight for choosing y = x + 5
Awesome solution
why do you take y=x+5 , why not x+4 or something else , can you brief me a little bit ?
Log in to reply
So that I get ( y − 1 ) ( y + 1 ) = y 2 − 1 and ( y − 2 ) ( y + 2 ) = y 2 − 4 . Other options are not possible. Why don't you try y = x + 4 .
Because y = x + 5 makes ( x + 3 ) ( x + 7 ) = ( y − 2 ) ( y + 2 ) = y 2 − 4 and ( x + 4 ) ( x + 6 ) = ( y − 1 ) ( y + 1 ) = y 2 − 1 , then ( y 2 − 1 ) ( y 2 − 4 ) = y 4 − 5 y 2 + 4 so eliminated the x 3 term and it becomes a quadratic equation which is easily solved.
But why (x+5)?
Log in to reply
Because 5 is not a subtrahend in any of the factors
Because y = x + 5 makes ( x + 3 ) ( x + 7 ) = ( y − 2 ) ( y + 2 ) = y 2 − 4 and ( x + 4 ) ( x + 6 ) = ( y − 1 ) ( y + 1 ) = y 2 − 1 , then ( y 2 − 1 ) ( y 2 − 4 ) = y 4 − 5 y 2 + 4 so eliminated the x 3 term and it becomes a quadratic equation which is easily solved.
best solution of all
Elegant solution
IT IS EASY by Factorization! 1120=4×5×7×8 or 1120=-4×-5×-7×-8 so x=1 or -11!( •̀∀•́ )
Log in to reply
You are right.
Log in to reply
Can you explain the step after factorisation in a bit more depth, please?
Log in to reply
@Sol Rey – Note that ( a − b ) ( a + b ) = a 2 − b 2 . Therefore, ( y − 1 ) ( y + 1 ) = y 2 − 1 and ( y − 2 ) ( y + 2 ) = y 2 − 4 ,
Why we ignore “ y^2 + 31=0 ?
Even simpler: the term on the left is symmetric around x=-5. It crosses the zero 4 times around x=5 and gets more positive for x<-7 and x>-3. It will cross y=1120 at some x1=-5-z and x2=-5+z. Then, x1+x2= -5-z+(-5+z)=-10. So we don't even need to calculate x1 and x2.
Log in to reply
Nice, this solves for a right range of values on the right.
How on earth do you people even think of these ideas on the spot?
darn i tried to use vietas and failed
When x=-10 is substituted the left hand side of the equation is 504 therefore x cannot equal -10
Log in to reply
You are right. The roots are 1 and − 1 1 . And the answer needed is the sum of roots (1-11 = - 10) and not x .
( x + 3 ) ( x + 4 ) ( x + 6 ) ( x + 7 ) = 1 1 2 0
( x + 3 ) ( x + 7 ) ( x + 4 ) ( x + 6 ) = 1 1 2 0
( x 2 + 1 0 x + 2 1 ) ( x 2 + 1 0 x + 2 4 ) = 1 1 2 0
Let x 2 + 1 0 x = a
( a + 2 1 ) ( a + 2 4 ) = 1 1 2 0
a 2 + 4 5 a + 5 0 4 = 1 1 2 0
a 2 + 4 5 a − 6 1 6 = 0
( a + 5 6 ) ( a − 1 1 ) = 0
⇒ a = − 5 6 o r a = 1 1
When a = − 5 6 ⇒ x 2 + 1 0 x + 5 6 = 0 ⇒ x = 2 − 1 0 ± − 1 2 4 which are complex roots , hence not considered.
When a = 1 1 ⇒ x 2 + 1 0 x − 1 1 = 0 , the discriminant is positive.
Hence by Vieta's formula , sum of real roots = − 1 0
I think that the RELATION to the picture in the question is that if we put y = x + 5 , the whole equation can be reduced to the quadratic equation, which can be further solved very easily.
Also, 5 is the average of 3 , 4 , 6 , 7 : listed in the problem.
You can also consider a = x 2 + 1 0 x + 2 1 .
a ( a + 3 ) = 1 1 2 0 ⟹ a 2 + 3 a − 1 1 2 0 = 0 ⟹ ( a + 3 5 ) ( a − 3 2 ) = 0 ⟹ ( x 2 + 1 0 x + 5 6 ) ( x 2 + 1 0 x − 1 1 ) = 0
The rest is the same as yours.
Log in to reply
Yeah. This is the same method as used in the continuation of the problem!
Can't we put x = 1? ( 1 + 3 ) ( 1 + 4 ) ( 1 + 6 ) ( 1 + 7 ) = 4 ∗ 5 ∗ 7 ∗ 8 = 1 1 2 0 Why isn't it correct?
Log in to reply
the question asks for the sum of all real x. -11 satisfies.
not the easiest.. enter x-5 instead of x. then ( x − 2 ) ( x − 1 ) ( x + 1 ) ( x + 2 ) = 1 1 2 0 it forms a bi-quadratic whose real root will always have a sum of 0. judging by the quadratic discriminant, it has 2. so n = 1 ∑ 2 ( x n − 5 ) = 0 → n = 1 ∑ 2 ( x n ) = 1 0
Can someone explain to me what Vieta's formula is? I am not a mathematical genius so please explain at a commoner level.
Log in to reply
The simplest case is for a quadratic equation, let's say a x 2 + b x + c = 0 , with a , b and c as the coefficients respectively, the sum of the two roots is equal to − a b and the product of the two roots is a c . For general cases, please check http://en.wikipedia.org/wiki/Vieta's_formulas
Log in to reply
Thanks. I knew the formula but I didn't know that it was called Vieta's formula. I got up to expanding the LHS but I was lost after that.
Log in to reply
@John Taylor – i did the same mistake that of yours...
Thanks a lot.....
@John Taylor , This might help you out. ⌣ ¨
why can't it be x=1?? then it would be (1+3)(1+4)(1+6)(1+7)=1120
Log in to reply
Note that the problem asks for the sum of all real solutions x . x = 1 is one of the (real) solutions. There's another one, namely x = ( − 1 1 ) . Their sum is ( − 1 0 ) , hence the answer.
I agree with you
Nice. Same method. Cheers!
What's the relation of − 1 0 with the picture?
Is it 5 × − 2 = − 1 0 ? @Mehul Arora
Log in to reply
TBH, I do not know that what is the relation. A moderator had probably changed the title of the problem. Initially, the problem was named, "That can't be tough, Can it?"
Log in to reply
OK, BTW , Sir Sandeep Bhardawaj found the relation!
Log in to reply
@Harsh Shrivastava – Yeah! He has a great observation.
I think the problem modifier wants to question the people 'where is 5?' Hence to complete the series 3,4,5,6,7 ,he added image of 5. :/
Log in to reply
That logic is also awesome like Sir Sandeep's logic!
I'd also like to point out that 1 also works for the answer, though it says it's wrong.
(1+3)(1+4)(1+6)(1+7)
= 4 x 5 x 7 x 8
= 20 x 56
= (20 x 50) + (20 x 6)
= 1000 + 120
= 1120
I'll point out that I got this answer by guessing, but I'm disappointed that it didn't work.
Log in to reply
1 is 1 solution. try -11. it asks for the sum.
It does work but you stopped just short. The only thing is that for the other solution (-11) the answers would have been -8, -7, -5 and -4 and the product would have been the same.
-11 not -10 ...correct, also +1 correct
why x is not equal to 1?
but if we multiply the terms and apply theory of polynomial equations we get x 4 + 2 0 x 3 + 1 4 5 x 2 − 6 1 6 = 0 and by theory of polynomial equations sum of roots is given by negative division coefficient of highest power of x upon coefficient of second highest power of x i.e -20
Log in to reply
Hi Jus,note that the problem asks for the sum of real roots of the given equation.
Log in to reply
OK so basically the method i used gives sum of all real unreal roots thus i got it wrong ? Well if thats the case thn thanks Mehul
Log in to reply
@Jus Jaisinghani – Yes! Vieta's formula gives the sum of all the real as well as complex roots. Thus, you got it wrong. Glad to be of assistance :)
Why we cant put 1? (1+3)(1+4)(1+6)(1+7)=1120 also!!!!!!!!
Log in to reply
Hi Shadman, the problem asks for the SUM of the solutions that satisfy the equation above. Indeed, one satisfies the equation, but there are other solutions too.
Why can't we do it by subsituting x=y-5
cant we just multiply all the monomials and apply the sum of roots formula to it, since the constant has no effect on the sum of roots of any polynomial
Log in to reply
No, because that would be the sum of ALL the roots and the questions asks for only the REAL roots
I could get x only equal to 1 and -10
I also did the same :)
@Christopher Boo Did you modify it? Please tell the logic behind 5!
Hi, I found a mistake: I check for x=-10 (-10+3)(-10+4)(-10+6)(-10+7)=(-7)(-6)(-4)(-3)= 504 5 0 4 = 1 1 2 0
I think that there is a mistake: x 2 + 1 0 x − 1 1 = 0 d e l t a = b 2 − 4 a c d e l t a = 1 0 0 + 4 4 = 1 4 4 d e l t a = 1 2 x 1 = 2 − 1 0 + 1 2 = 1 x 2 = 2 − 1 0 − 1 2 = − 1 1
And I solved this task: I consider: a= x+5 ( a − 2 ) ( a − 1 ) ( a + 1 ) ( a + 2 ) = 1 1 2 0 ( a 2 − 4 ) ( a 2 − 1 ) = 1 1 2 0 a 4 − 5 a 2 − 1 1 1 6 = 0 I consider: a 2 = t , where 0 < t < + ∞ t 2 − 5 t − 1 1 1 6 = 0 d e l t a = 2 5 + 1 1 1 6 × 4 = 4 4 8 9 d e l t a = 6 7 t 1 = 2 5 + 6 7 = 3 6 t 2 = 2 5 − 6 7 = − 3 1 (It's not OK.) So t=36 \ --> a 2 = 3 6 --> a=6 or a=-6 --> x= -11 or x= 1
What do you think about my solution?
Log in to reply
"Find the sum of all real satisfying the equation above"
Nobody said x = -10. It was -11. So the answer to the original question i.e. sum of the real roots is -10
We have ( x + 3 ) ( x + 4 ) ( x + 6 ) ( x + 7 ) = 1 1 2 0 . Let x + 5 = z . The expression becomes ( z − 2 ) ( z − 1 ) ( z + 1 ) ( z + 2 ) = 1 1 2 0 .
( z 2 − 4 ) ( z 2 − 1 ) = 1 1 2 0
z 4 − 5 z 2 + 4 = 1 1 2 0
z 4 − 5 z 2 − 1 1 1 6 = 0
( z 2 − 3 6 ) ( z 2 + 3 1 ) = 0
The only real values of z for which this equation is true is z = 6 and z = − 6 . x = z − 5 so the real x satisfying this equation are x = 1 and x = − 1 1 .
1 + − 1 1 = − 1 0
We factor 1120 into 7x5x2^5=1120.
With a little playing around one can easily find that one positive solution would be 4,5,7 and 8. Where x=1.
We are not done yet. It also appears there could be a negative solution also for this. We then further rule out 2 negatives and 2 positives because that cannot be consistent with the equation. Thus the only solution must have the characteristics of 4 negatives.
Then again there are two possibilities. We already know that the numbers are 4,5,7 and 8 but we don't know which 'way' the equation starts at. In other words does -4=x+3 or -8=x+3? We test the later and find that it works thus giving us x=-11.
We add 1+(-11) together and get -10, our answer.
I solved it in the same way, but how can we know for sure that these two are the only solutions? The problem states that x is a real number, not a whole number
Log in to reply
I realized that there was probably only two real integer solutions because of the constraints given. When you see that the factors are in increasing order, they thus must be in intervals of 1 or 2. From there I rationalized that if a number was irrational then it would have a conjugate which would be x less which would invalidate the original condition. The numbers must strictly be increasing in order by steps of 1 or 2 AND be all positive or negative.
If x wasn't whole the multiplication wouldn't have a whole answer.
How did your prove that 2 negatives and 2 positives cannot be consistent with the equation ?? Can you explain more explicit please
This is about how I solved it.
I love this solution ....easy and straightforward
Log in to reply
Thank you so much that you love my solution.
1 1 2 0 = 4 ∗ 5 ∗ 6 ∗ 7 s o i f x + 3 = 4 w e g e t t h e s o l u t i o n x = 1 . . N o w t h e c o n s t a n t t e r m i s b y V i e t a ′ s F o r m u l a = 3 ∗ 4 ∗ 6 ∗ 7 − 1 1 2 0 = − 6 1 6 = − p r o d u c t = − 7 ∗ 8 ∗ 1 1 . I f x = ± 7 , ( 7 + 6 ) = 1 3 o r ( − 7 + 4 ) = − 3 n o t f a c t o r s o f 1 1 2 0 . I f x = ± 8 , ( x + 7 ) = 1 5 n o t a f a c t o r 1 1 2 0 b u t − 8 i s . I f x = ± 1 1 , ( 1 1 + 4 ) = 1 5 i s n o t a f a c t o r o f 1 1 2 0 b u t − 1 1 i s . B u t w i t h x = − 8 , t h e p r o d u c t o f f o u r b r a c k e t s i s n o t 1 1 2 0 . B u t w i t h x = − 1 1 , t h e p r o d u c t o f f o u r b r a c k e t s i s 1 1 2 0 . Now the sum of all roots = -(3+4+6+7)= - 20. So the sum of the remaining two roots is = -20 +1 - 11= -10. So other roots can be 1, and -11. That means the expression is a square., but the last is - tive and not a square. So other two roots are not real. Sum of real roots =1 + (-11) = - 10.
I think you wanted to say 1 1 2 0 = 4 × 5 × 7 × 8 = 4 × 5 × 6 × 7 . Also, − 1 1 doesn't divide 1 1 2 0 , but − 1 1 + 4 = − 7 does.
The relation with the picture is that there is no x + 5 term, and hence, one substitutes x = t − 5
We have, after the substitution,
( t − 2 ) ( t − 1 ) ( t + 1 ) ( t + 2 ) = 1 1 2 0 ⟹ ( t 2 − 1 ) ( t 2 − 4 ) = 1 1 2 0
Further substitute s = t 2 . Then,
( s − 1 ) ( s − 4 ) = 1 1 2 0 ⟹ s 2 − 5 s − 1 1 1 6 = 0
Since we have real numbers in play here, use the Quadratic Formula, to get:
s = 2 5 ± 4 4 8 9 = 2 5 ± 6 7 ⟹ s = 3 6 or − 3 1
⟹ t 2 = 3 6 or − 3 1 (rejected, since t 2 > 0 ) ⟹ t = ± 6
⟹ x = ± 6 − 5 = 1 or − 1 1
Hence, x ∈ ℜ ∑ x = − 1 0
I have a non-standard but relatively quick solution to the problem.
Prime factorise 1120 and you get 2 5 × 5 × 7 which can be rewritten as 4×5×7×8.
Note that this is exactly in the format of the LHS expression, clearly x = 1 is a solution.
But consider − 8 × − 7 × − 5 × − 4 as a possibility thus x = − 1 1 is a solution too. Adding both gives you the required answer.
Yes sir. Same method :)
I found this fairly easy to be solved just by inspection.
The prime factors of 1120 are 2 5 , 5 and 7, so it's easy to see that one of the solutions is x = 1. For the other solution, each of the four factors must be the negative equivalents of all the four factors (4, 5, 7 and 8), so x = -11.
Note that x cannot take any other value because each of the factors are in the from of (x + a), and so there is only one combination of real numbers that will produce any real product.
Let (x+5)=a . (a-2)(a-1)(a+1)(a+2)=1120.
Why do this? How does it help?
As many earlier solutions have noted, we can use the prime factorization of 1120 to quickly find two solutions.
1 1 2 0 = 2 5 ∗ 5 ∗ 7
1 1 2 0 = 3 2 ∗ 3 5
1 1 2 0 = 4 ∗ 5 ∗ 7 ∗ 8 = − 8 ∗ − 7 ∗ − 5 ∗ − 4
By inspection, we see that the first factorization gives us x = 1, while the second gives us x = -11.
To see that there are no other real solutions, consider the graph of
f ( x ) = ( x + 3 ) ( x + 4 ) ( x + 6 ) ( x + 7 )
This is a quartic with a positive leading coefficient and four zeros at -7, -6, -4 and -3 (i.e. it looks like a W.) Thus it has to intersect the line y=1120 at least twice, once to the left of the four zeros and once to the right. Any other intersections of the two graphs would have to occur between the two middle zeros (as between -7 and -6, as well as between -4 and -3, the graph lies below the x-axis.)
By symmetry, the maximum value for f(x) between the middle zeros must occur at x = -5; but f(-5) = 4, so the graphs do not intersect anywhere other than the two points mentioned earlier, and thus x = -11 and x = 1 are indeed the only real solutions to the given equation.
First, notice that x ≥ 6 because:
( 6 + 3 ) ( 6 + 4 ) ( 6 + 6 ) ( 6 + 7 ) = 6 4 + O ( 6 ) + 3 × 4 × 6 × 7 = 1 2 9 6 + O ( 6 ) + 5 0 4 > 1 1 2 0
Then, after plugging in some values we find that x = 1 works, and since there is an even number of factors, we can obtain the same result with negative numbers due to the fact that 7 + 3 = 1 0 , and 6 + 4 = 1 0 , which can be "inverted" to get the same numbers but with opposite sign when subtracting 1 0 . And to get the same factors we subtract 1 again, hence x = − 1 0 − 1 = − 1 1 works too.
So the sum is: − 1 1 + 1 = − 1 0
If you think of the 1120 as the area of a rectangle.
You can arrange the two sides of the rectangle as (x+3)(x+7) and (x+4)(x+6).
When you multiply out the brackets, you are left with x^2+10x+21 as one side and x^2+10x+24 as the other.
The latter can then be written as x^2+10x+(21+3).
Therefore the area of the rectangle can be found to be (x^2+10x+21)^2 + 3(x^2+10x+21) = 1120.
Then by Substituting x^2+10x+21 for y. You get y^2+3y-1120=0.
When solving this equation you get 2 solutions 32 and -35.
Then when you substitute x^2+10x+21 back in and try to solve when = to 32 and -35. The solution for when = 32 is -11 and 1 and there is no real solution for when = -35.
So the answer is -11 + 1 which is -10.
Notice that 1 1 2 0 = 2 5 × 5 × 7
If we compare and rearrange with the L H S expression, we can see:
( x + 3 ) ( x + 4 ) ( x + 6 ) ( x + 7 ) = 2 3 × 2 2 × 5 × 7
⇔ ( x + 3 ) × ( x + 6 ) × ( x + 4 ) × ( x + 7 ) = 4 × 7 × 5 × 8
This implies that we need to find x such that it "fits" (or so-called 'symmetric to-') the arrangement on the R H S . We can see that x = 1 is an answer. However, we must check another way that we can arrange this.
We try to attain x to a negative value. By doing this we have:
[ − 1 ( x + 3 ) ] [ − 1 ( x + 4 ) ] [ − 1 ( x + 6 ) ] [ − 1 ( x + 7 ) ] = 2 3 × 2 2 × 5 × 7
( − x − 3 ) ( − x − 4 ) ( − x − 6 ) ( − x − 7 ) = 4 × 7 × 5 × 8
Eyeballing for x gives us x = − 1 1
The reason why we do this is because of these two possible factorizations of 1 1 2 0 :
-
− 2 3 × − 2 2 × 5 × 7
-
− 2 3 × − 2 2 × − 5 × − 7
which have negative values that could accord to the products of the terms in the L H S polynomial, but gives the value of a positive integer. We see that the first option on the list is not symmetric to the L H S polynomial, hence not a feasible factorization. Second option is possible because it is symmetric to the L H S polynomial since its just every term in the product times − 1 .
Therefore, the sum of all solution to x is − 1 1 + 1 = − 1 0
Simply separate 1120 into primes. Note: 5, 7, 2^2, 2^3. Since there are even number of factors two solutions exists; the above values for positive and negative. Which only occurs for 1 and -11; 1 + - 11 = -10.
By analysis, we can see that it will have 2 real roots . Let they be a and b. As product has 4 terms , negative sign gets compensated. We have , (a+3)=-(b+7) , (a+4)=-(b+6) , and so on. Solving any one, we get a+b=-10.
Probably should have solved it using algebra... but that's no fun. Instead, here's a numerical method.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
|
( x + 3 ) ( x + 4 ) ( x + 6 ) ( x + 7 ) = ( x + 3 ) ( x + 7 ) ( x + 4 ) ( x + 6 )
( x + 3 ) ( x + 4 ) ( x + 6 ) ( x + 7 ) = ( x + 5 − 2 ) ( x + 5 + 2 ) ( x + 5 − 1 ) ( x + 5 + 1 )
( x + 3 ) ( x + 4 ) ( x + 6 ) ( x + 7 ) = ( ( x + 5 ) 2 − 4 ) ( ( x + 5 ) 2 − 1 )
1 1 2 0 = 3 2 ⋅ 3 5 = ( − 3 2 ) ⋅ ( − 3 5 )
So we've obviously got 4 solutions, the two solutions of ( x + 5 ) 2 = 3 6 , which are 1 and -11, and the two solution of ( x + 5 ) 2 = − 3 1 which aren't real.
Since this is an equation of degree four, they are all the solutions there are.
Make the equation above becomes : ( 4 ) ( 5 ) ( 7 ) ( 8 ) = 1 1 2 0 or ( − 8 ) ( − 7 ) ( − 5 ) ( − 4 ) = 1 1 2 0
Therefore ( x = 1 ) and ( x = − 1 1 ) So , The Answer is ( 1 − 1 1 = − 1 0 )
Consider that if (x+3)=-(y+7), x and y real roots, we have the same numbers being multiply with negative signal, but as (-1)^4=1 it gives the same number.
x+3=-y-7
x+y=-7-3
x+y=-10
take (x+5=y)....then we shall get the equation simlified as, (y^4)-(y^2)-1116=0..........now by middle term factorisation we get (y^2)=36...i.e y=6,-6....x=y-5=1,-11 therefore the sum is -10
If y=x+5
Then the equation became
(y-2)(y-1)(y+1)(y+2)=1120
(y-2)(y+2) (y-1)(y+1)=(y-2^2)(y^2-1^2)
y^4-5y^2+4=1120
Bhaskara for y^2
y^2=36 or y^2=-31
Only real solutions
y=6 or y=-6
So x=1 or x=-11
Finally
-11+1=-10
The function y=(x+3)(x+4)(x+6)(x+7) has -5 as its medium point and the function is symetric around it. The function has 4 roots. For values bigger than --3 or less than -7 increases. For most of values of y there are two solutions that are at the same distance from -5 and the sum of them is always -10. Someone could proof it mathematically.
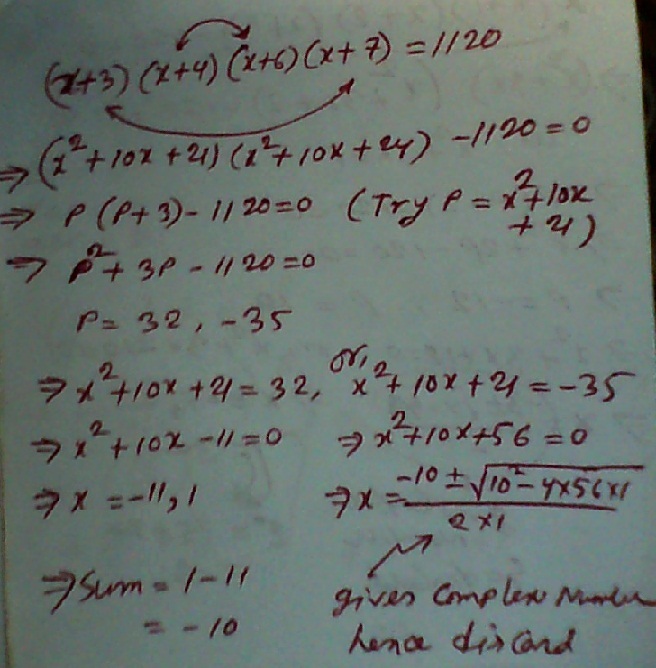
Simpler solution by @XerDazzle XD酱 as follows:
( x + 3 ) ( x + 4 ) ( x + 6 ) ( x + 7 ) = 1 1 2 0 = 4 × 5 × 7 × 8 ⟹ { x = 1 x = − 1 1 ⟹ ( 1 + 3 ) ( 1 + 4 ) ( 1 + 6 ) ( 1 + 7 ) = 4 × 5 × 7 × 8 ⟹ ( − 1 1 + 3 ) ( − 1 1 + 4 ) ( − 1 1 + 6 ) ( − 1 1 + 7 ) = ( − 8 ) ( − 7 ) ( − 5 ) ( − 4 )
Therefore, sum of solutions is 1 − 1 1 = − 1 0 .
Previous solution
Let y = x + 5 (see note), then:
( x + 3 ) ( x + 4 ) ( x + 6 ) ( x + 7 ) ( y − 2 ) ( y − 1 ) ( y + 1 ) ( y + 2 ) ( y 2 − 1 ) ( y 2 − 4 ) y 4 − 5 y 2 + 4 y 4 − 5 y 2 − 1 1 1 6 ( y 2 + 3 1 ) ( y 2 − 3 6 ) ⇒ y ⇒ x = 1 1 2 0 = 1 1 2 0 = 1 1 2 0 = 1 1 2 0 = 0 = 0 = ± 6 = { − 6 − 5 6 − 5 = − 1 1 = 1
Therefore the sum of x satisfying the equation = − 1 1 + 1 = − 1 0
Note that 5 is the arithmetic mean of 3, 4, 6 and 7. Using y = x + 5 results in the four factors y ± 1 and y ± 2 , so that we eventually get a quadratic equation y 4 − 5 y 2 + 4 = 1 1 2 0 without the y 3 and y terms, which can be easily solved.