Resistors!
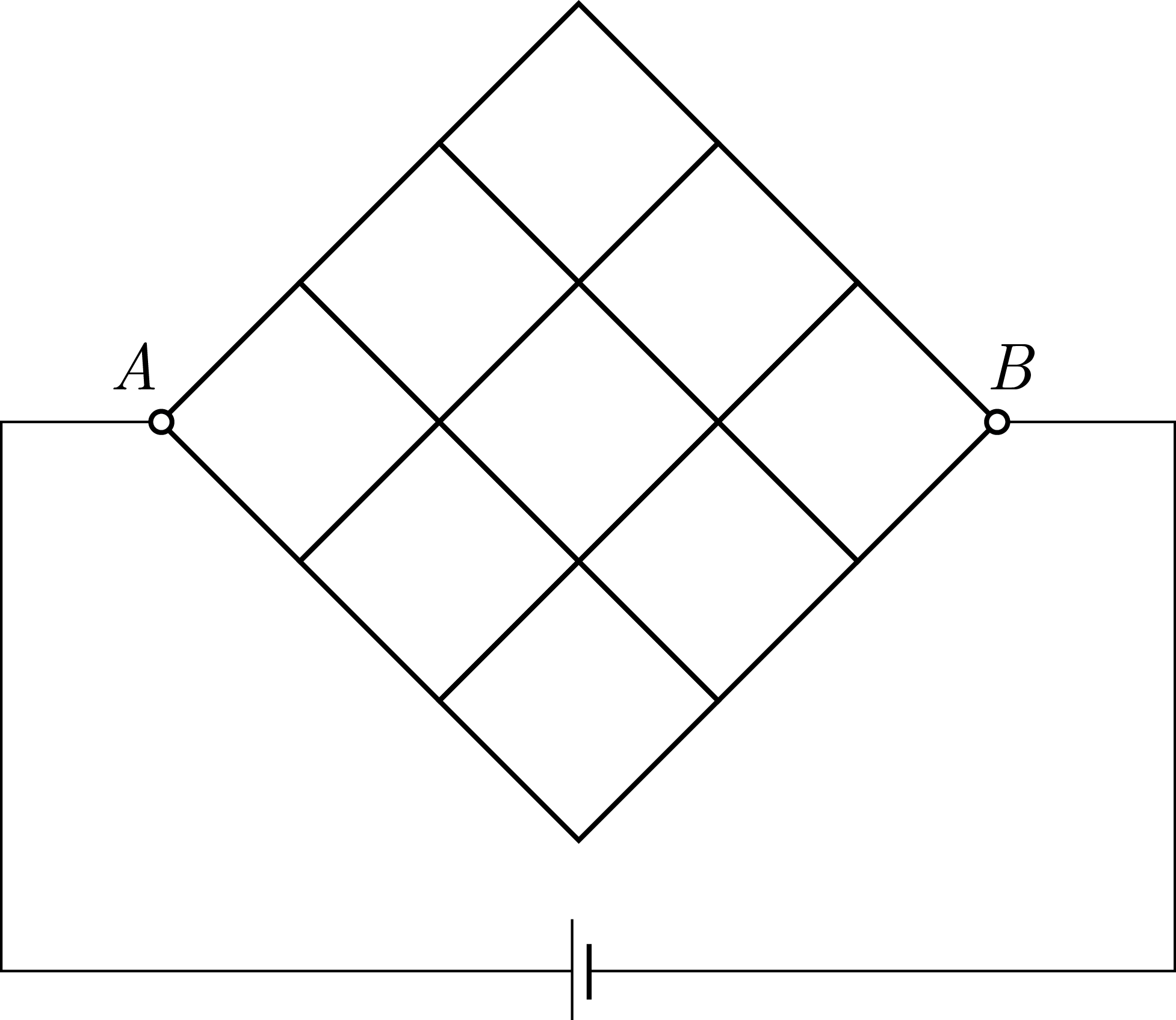
As seen above, a set of resistors are arranged in forms of the cells, each side having a resistance R . If R 0 represents between the two points A and B . If R R 0 = b a for coprime positive integers, find the value of
a + b + a b .
The answer is 111.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Moderator note:
Terrific topological solution. Can you justify your logic at the second use of symmetry?
I Am Getting Correct Answer By This Method But When I Am Trying To Solve It Using Basics( Symmetry Method ) I Am Getting Answer As 11/6 . (Which Is Very very close to 13/7 when i checked calculator). but i am wondering why i am getting wrong answer by that method (I Did it 3 times but repeatedly go answer as 11/6)
Log in to reply
Lets Say If We Do Not Fold The Circuit. Then As You Have Said Too That By Symmetry Along Line CD We Can Remove The Junction At O.So The Equivalent Resistance Of The Cell Above O Will Be R . Similarly The Equivalent Resistance of the 2 cells that lie vertically below O Will Also Be R . Now These Three Will Be In Parallel Combination.Similarly If We Go On Reducing The Circuit I AM Getting Answer As 11/6
Log in to reply
Resistance of the combination below will be 2 R and above will be 2 3 R . Think it up again!
Log in to reply
@Kishore S. Shenoy – How Can You Please Explain In A Bit Detail . ( I Think For The Cell Which is directly above O Will Be R And for the two cells which are vertically below will be R Each) .
Log in to reply
@Prakhar Bindal – See, Cells above the vertical line of O will be in the form \chemfig − 2 R ( − [ : 4 5 ] R ) ( − [ : − 4 5 ] R ) − 2 R − = 2 R + 2 R + 2 R = 2 3 R
And below − 2 R − 2 R − 2 R − 2 R − = 2 4 R
Click here
to see how
\chemfig
renders...
Log in to reply
@Kishore S. Shenoy – Used the same method as you. I love when symmetry makes questions easier. Someone who looks at this question for the first time will get nervous because of complex system, until he realises how easy it has become due to symmetry. :D
As in symmetry, you combine the middle layer of the once folded combination. That step makes you wrong. You should notice one thing that you can use symmetry only when the folded surfaces are having equal potential...
@Brilliant Physics , the logic is that if we reverse the current, since the Circuit is symmetric, current flowing through a typical wire resistor will be same in both the cases. So we can split the junction!
Log in to reply
I'm thinking, is there a simple physical reason for why we can make the split, i.e. is there a reason no current flows across the point O from I 1 to I 4 .
Log in to reply
Yes, both are in equal potential. i.e. at O , I 4 and I 2 are having same potential.
Log in to reply
@Kishore S. Shenoy – What do you mean in saying that the currents have the same potential?
Log in to reply
@Brilliant Physics – At point O, all routes possible routes to B have same resistance. So we can "consider" them to have equal potential.
Log in to reply
@Kishore S. Shenoy – Got it. I think that is the physical insight some people might have been wondering about. Terrific problem and solution.
I am amazed by the work you put in to post a question and the solution. I mean just look at images you have posted .. WOW
I have a slightly different solution.
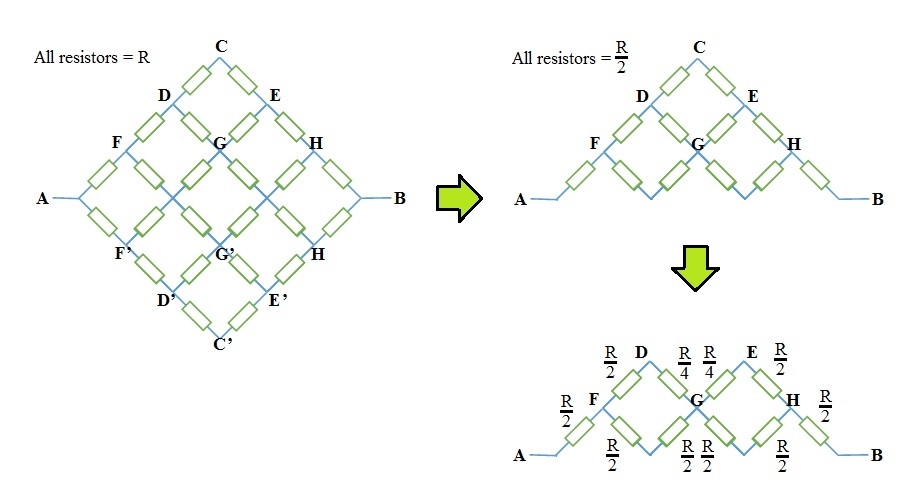
Due to symmetry, we note that points C, D, E, ... have the same potential with the respective C', D', E'. Therefore, they can be considered as same points and hence the equivalent circuit of 1 2 × R ∣ ∣ R or 2 R resistors.
Again due to symmetry we note that both the potentials of C and G are 2 1 V A B , therefore they can be considered as a same point and hence the second equivalent circuit with 2 × 4 R .
Therefore,
R 0 ⇒ R R 0 = 2 × ( 2 R + ( 2 R + 4 R ) ∣ ∣ ( 2 R + 2 R ) ) = 2 × ( 2 R + ( 4 3 R ) ∣ ∣ ( 1 ) ) = 2 × ( 2 R + 4 3 R + R 4 3 R × R ) = 2 × ( 2 R + 7 3 R ) = 7 1 3 R = 7 1 3
⇒ a + b + a b = 1 3 + 7 + 1 3 × 7 = 1 1 1
I doubt whether C and G are having equal potential. Can you explain without using symmetry?
Log in to reply
Got it, no problem! Thanks for the solution!
Same method !
Thing that should have been clearer in description was R as resistance onto side of smallest unit of square! Let this be a summary:
R 0 = [~ R ~(3 R // 4 R )~ R ~] // [~ R ~(4 R // 3 R )~ R ~] = [ 3 + 4 3 × 4 R + 2 R ] // [ 4 + 3 4 × 3 R + 2 R ] = 7 2 6 R × 2 1 = 7 1 3 R
13 + 7 + 13 × 7 = 111
Answer: 1 1 1
First let us consider symmetry along A B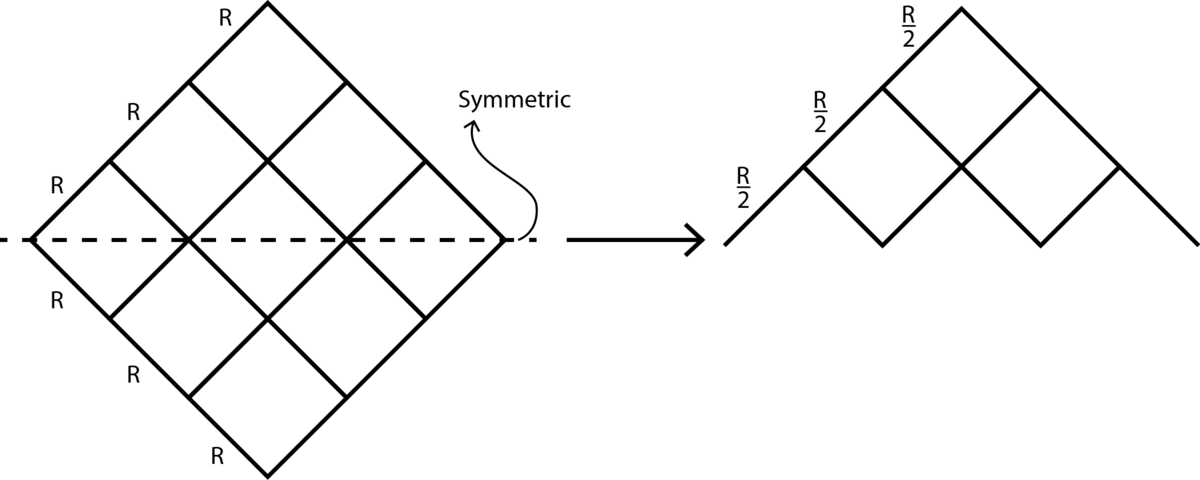
Since the arrangement is symmetric about A B , we can fold the plane to make overlapping resistors connected parallely.
Now the folded image is symmetric about C D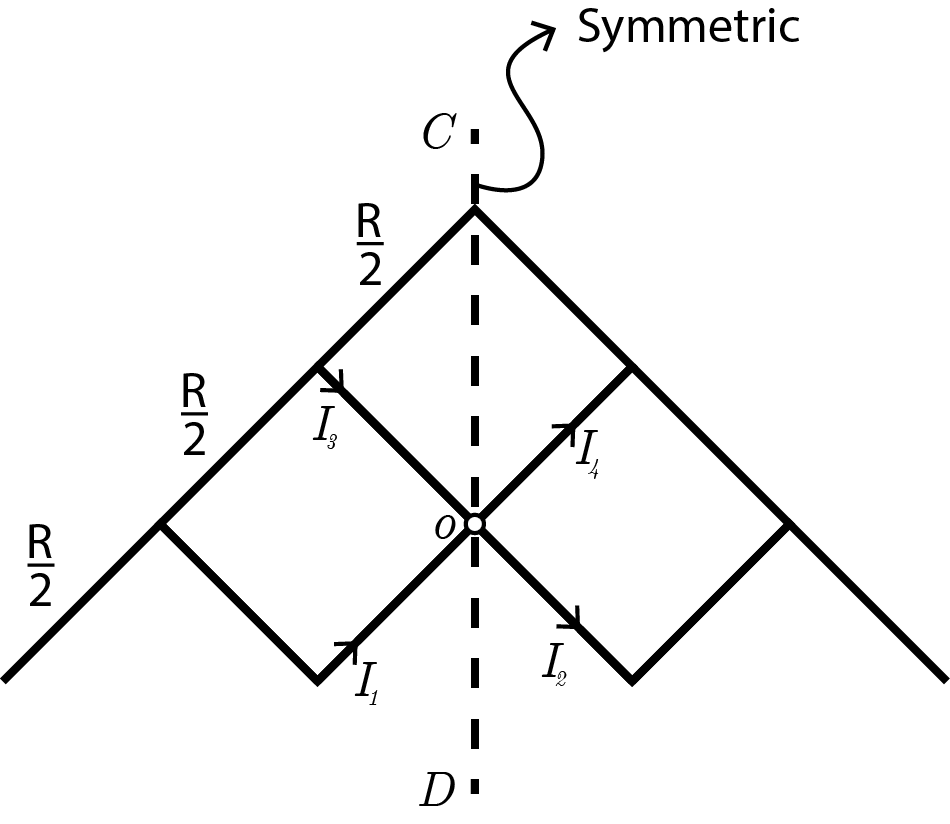
So, I 1 = I 2 and I 3 = I 4 , and hence we can split the arrangement at O .
Now, the arrangement can be further modified into:
So, R 0 = 2 R + 3 R 2 + 4 R 2 1 + 2 R = 7 6 R + R = 7 1 3 R
∴ R R 0 = 7 1 3