That looks like a moon!
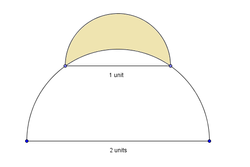 A semi circle of diameter 1 unit sits at the top of a semi circle of diameter 2 units. the shaded region inside the the semi circle but outside the larger semi circle is called a
lune
. If the area of the lune is
α
, then find the value of
⌊
1
0
0
0
α
⌋
A semi circle of diameter 1 unit sits at the top of a semi circle of diameter 2 units. the shaded region inside the the semi circle but outside the larger semi circle is called a
lune
. If the area of the lune is
α
, then find the value of
⌊
1
0
0
0
α
⌋
Note
- Assume that the diameters are parallel to each other.
The answer is 302.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Can you explain why " - 1/3(area of greater semi circle)"? How do you know that the corresponding area should be 1/3?
Log in to reply
Extend two lines from the centre of the diameter of the bigger circle to the two ends of the chord of length 1,just opposite to it. We thus have an equilateral triangle of length 1,each. Angles for an equilateral triangle is pi/3. Hence the sector is 1/3 of the semi circle.
Log in to reply
Right. So, as opposed to "1/3 (area of greater semi circle)", you actually mean " 1/3 area of greater semi circle - equilateral triangle of length 1".
I see that this is expressed in the 2nd equation in terms of "(pi/6 - root 3 / 4)"
If you agree with this, can you update the solution accordingly?
Log in to reply
@Calvin Lin – Area of lune =area of smaller semi circle - (1/3(area of bigger semi circle) - area of the equilateral triangle)
Log in to reply
@Nayanmoni Baishya – Thanks. I have updated your solution accordingly. Note that you can edit your solution and comments by clicking on the "edit" icon at the bottom.
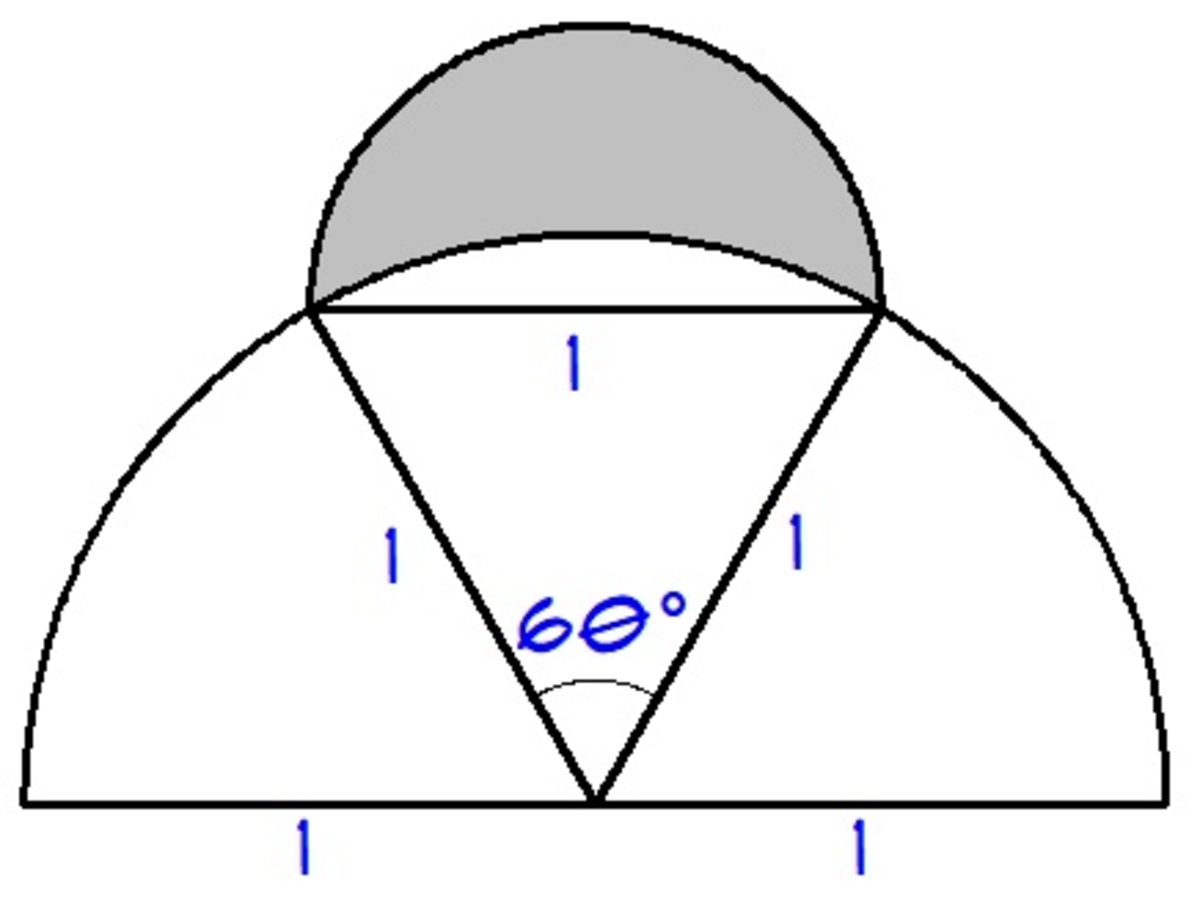 The area of the shaded part is area of the small semicircle minus the area of the segment of a circle(big). The area of the segment of the circle (big) is equal to the area of the sector of the circle minus area of the triangle.
The area of the shaded part is area of the small semicircle minus the area of the segment of a circle(big). The area of the segment of the circle (big) is equal to the area of the sector of the circle minus area of the triangle.
A s e g m e n t = 3 6 0 6 0 π ( 1 2 ) − 2 1 ( 1 2 ) ( sin 6 0 ) ≈ 0 . 0 9 0 5 8 6 0 7 3
A s h a d e d = 2 1 ( 4 π ) ( 1 2 ) − 0 . 0 9 0 5 8 6 0 7 3 ≈ 0 . 3 0 2 1 1 3 0 0 8
The desired answer is 1 0 0 0 ( 0 . 3 0 2 1 1 3 0 0 8 ) = 3 0 2
So we all know that using a calculator for this would be fraudulent and not in the spirit of mathematics.
Also can be solved using integrals,but it is harder...
Area of lune =area of smaller semi circle - (1/3(area of bigger semi circle) - area of the equilateral triangle) = (Pi/8)-(pi/6-root3/4)=a,
A=0.3021