That red triangle is so isolated!
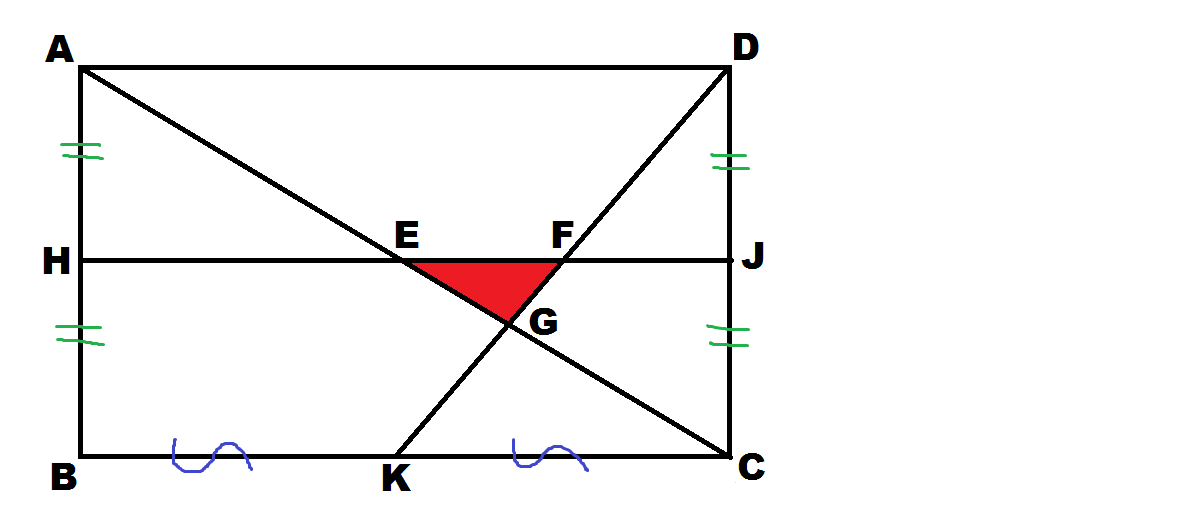
In rectangle A B C D , K , H , J are the mid-points of B C , A B , D C respectively. Line-segments A C , H J , D K bound a red triangle E F G . Find the ratio of the area of the big rectangle to the area of red triangle. Give your answer to correct 2 decimal places.
This problem is original.
The answer is 48.0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Moderator note:
I disagree with the first line. We do not know yet that H J ∥ B C . However, what we know is that "H, J is the midpoint of AB, CD" as given in the problem. Thus, it should be "Since H and J are midpoints of AB and CD, hence H J ∥ B C ".
It is important that the order of your logical deductions is presented correctly, so that others can easily follow what you are trying to say.
did exactly same way!! :-)
Log in to reply
I used co-ordinate geometry. Considered a rectangle with one vertex at origin, and others at ( 4 , 6 ) , ( 0 , 6 ) , ( 4 , 0 ) Found the area of red triangle and took the ratio.
Log in to reply
I think you did it with easiest way, but both are easy!!
Log in to reply
@Atul Shivam – I feel both the methods are easy, coordinate might be more easier. But I don't think there is great risk in errors in pure geometry solution, since there are hardly any numbers in it.
Log in to reply
@Nihar Mahajan – Ok bro edited my comment!!!
Log in to reply
@Atul Shivam – LOL, there was no need to xD
Log in to reply
@Nihar Mahajan – I think this should be level 4 , not 5.
Log in to reply
@A Former Brilliant Member – I think I had set it level 4, not 5.
Log in to reply
@Nihar Mahajan – Yes u r ri8!!! When I solved than “Solution writing guide was Level 4.
Log in to reply
@Atul Shivam – Experienced something similar , before i started it was level 4, after solving when I entered my ans. and got correct I noticed it became lvl 5 :P
I also did the same
A level 5 problem based on simple basic conceptual understanding.. nice one:))
I did it with a similar approach but messed up with the calculations as well as interpretation of the question.
First 2 times I entered the reverse ratio i.e. area of triangle to the area of rectangle And third time when I knew what to do, I messed up the calculations.
I did it like this:
AREA OF EFG= 1/4 AREA OF EKC = 1/16 AREA OF AGD
ALSO, AREA OF AHE= 1/8 AREA OF ABCD AND AREA OF DFJ= 1/16 ABCD
NOW, SINCE AREA OF AHJD IS HALF OF AREA OF ABCD, WE CALCULATE THE AREA OF AEFD AS 5/16 OF ABCD.
NOW, AREA OF AEFD= 15×AREA OF EFG===>5/(16×15) ABCD = AREA OF EFG
1/48 AREA OF ABCD= AREA OF EFG.
SO, THE REQUIRED RATIO IS
4
8
Nice logicy problem.
How did you found this gr8 configuration?
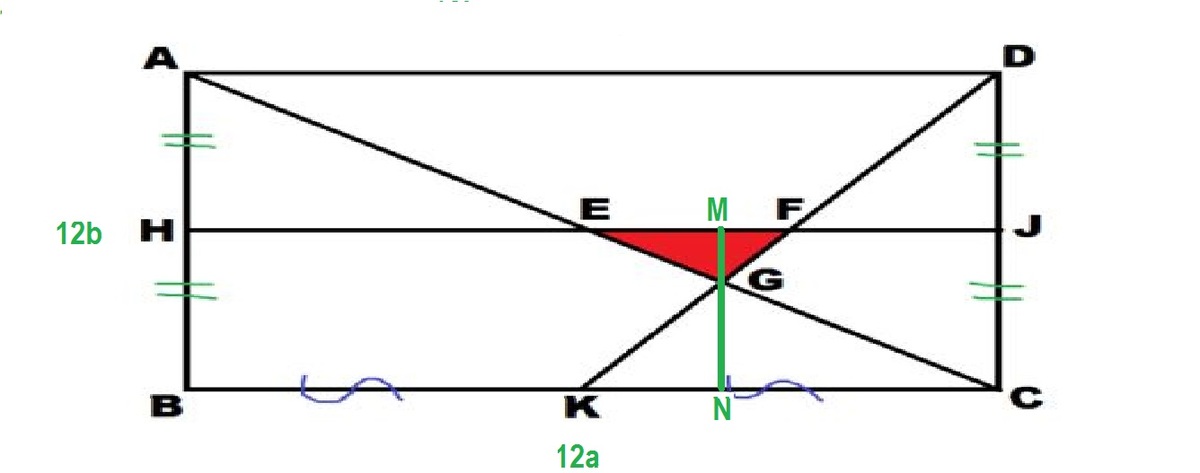L
e
t
A
B
=
1
2
b
,
a
n
d
B
C
=
1
2
a
.
∴
a
r
e
a
o
f
A
B
C
D
=
1
4
4
a
b
.
D
r
a
w
N
M
⊥
B
C
,
N
o
n
E
F
,
M
o
n
E
C
.
S
i
n
c
e
H
B
=
a
n
d
∣
∣
J
C
,
H
J
∣
∣
B
C
,
a
n
d
d
i
a
g
o
n
a
l
s
i
n
t
e
r
s
e
c
t
a
t
E
,
s
o
E
i
s
m
i
d
p
o
i
n
t
o
f
A
C
,
D
B
,
a
n
d
H
J
.
E
F
∣
∣
B
E
,
E
m
i
d
p
o
i
n
t
o
f
D
B
s
o
E
F
=
B
K
/
2
=
3
a
.
Δ
F
E
G
~
Δ
K
C
G
,
∴
N
G
G
M
=
F
E
K
C
=
3
a
6
a
=
2
∴
2
+
1
1
=
G
M
+
N
G
N
G
=
J
C
N
G
,
⟹
N
G
=
3
6
b
=
2
b
.
A
r
e
a
F
E
G
=
2
1
∗
E
F
∗
N
G
=
3
a
b
.
A
r
e
a
F
E
G
A
r
e
a
A
B
C
D
=
3
a
b
1
4
4
a
b
=
4
8
Please post it soon! I am eager to know it :)
Sir in 5th line it should be EF || BK not EF || BE .
I did it a separate way by visualising this shape on a y-x graph, you can find the coordinates of what would be the corners of your shape and the equations of the line intersecting them, using any value for the lengths of the rectangle, you can then find out the coordinates of the three edges of the red triangle, find out its area, and then compare it to the area of the triangle.
The same. This is known as coordinate geometry.
Since H J ∣ ∣ B C , J is midpoint of D C by Midpoint theorem D F = F K Also since E is mid-point of B D again by Midpoint theorem E F = 2 B K = 2 C K
We easily see that Δ E G F ∼ Δ C G K and since E F = 2 C K we have [ C G K ] [ E F G = 4 1 .Suppose [ E F G ] = x ⟹ [ C G K ] = 4 x We also get G C E G = [ G K C ] [ E G K ] = 2 1 ⟹ [ E G K ] = 2 x .Thus, [ E K C ] = [ E G K ] + [ K G C ] = 2 x + 4 x = 6 x which is exactly 1/8th area of total rectangle. Thus area of rectangle = 8 × 6 x = 4 8 x which is 4 8 times the area of red triangle. Hence ratio is 4 8 .