That was an obvious answer...
The area between the graphs of
f
(
x
)
=
x
and
g
(
x
)
=
x
for
0
≤
x
≤
1
is shaded in
r
e
d
. A slider, representing the function
h
(
x
)
=
c
, cuts this shaded area into two parts. Find the constant
c
for which
h
(
x
)
cuts the colored region in half.
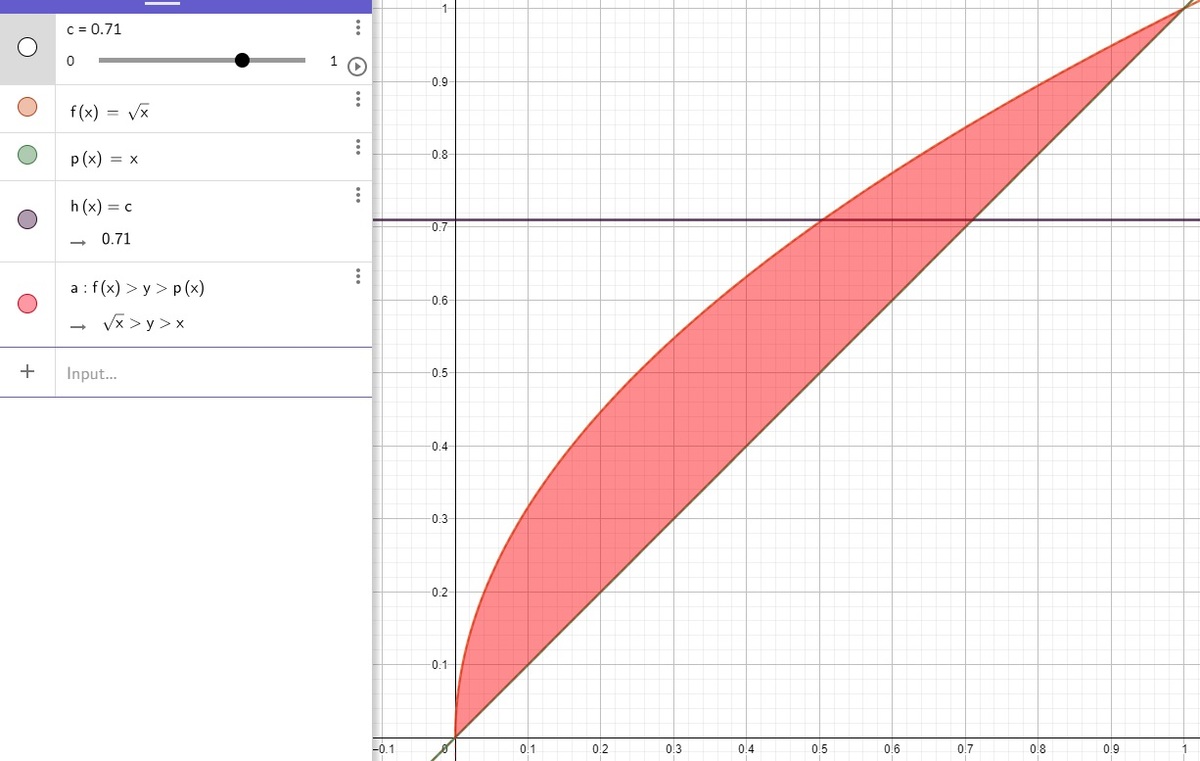
The answer is 0.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Can you explain what " y s " is? Without understanding your notation you seem to be saying that the formula for y s is y s : = 2 A 1 × A but this will always be 2 1 .
Log in to reply
I am sorry of course I will explain. It is the notation for the y-coordinate of the center of gravity and the line which halves the area must go through this coordinate
Log in to reply
All right. We should keep in mind that this is only true due to a symmetry that implicitly appears in the problem.
For instance, the x-coordinate of the center of gravity is 5 2 , but the line x = 5 2 doesn't split the area in half but rather, the split is about 5 3 % v 4 7 % .
Let's consider the equivalent problem which has f ( x ) = x 2 and g ( x ) = x . First, they intersect each other in ( 0 , 0 ) and ( 1 , 1 ) , and f ( x ) < g ( x ) for 0 < x < 1 . Hence we want to find c such that
∫ 0 c x d x − ∫ 0 c x 2 d x = ∫ c 1 x d x − ∫ c 1 x 2 d x
or, equivalently,
2 ∫ 0 c x d x − 2 ∫ 0 c x 2 d x = ∫ 0 1 x d x − ∫ 0 1 x 2 d x
Therefore:
2 2 c 2 − 2 3 c 3 = 2 1 − 3 1
⇒ 4 c 3 − 6 c 2 + 1 = 0
It's easy to see that 2 1 is a solution. That was an obvious answer, indeed!
Sorry for too much work but this is just another basic approach towards this problem, while I am aware there are easier methods I would like to present my own
bit
.
In this method, to get the y co-ordinate of the point where area is half we use inverse of the function
finding the area difference of corresponding inverse functions from [0,1]
Inversing functions are similar to flipping x and y axes , so we will end up with a parabola and a straight line with decreasing slope,
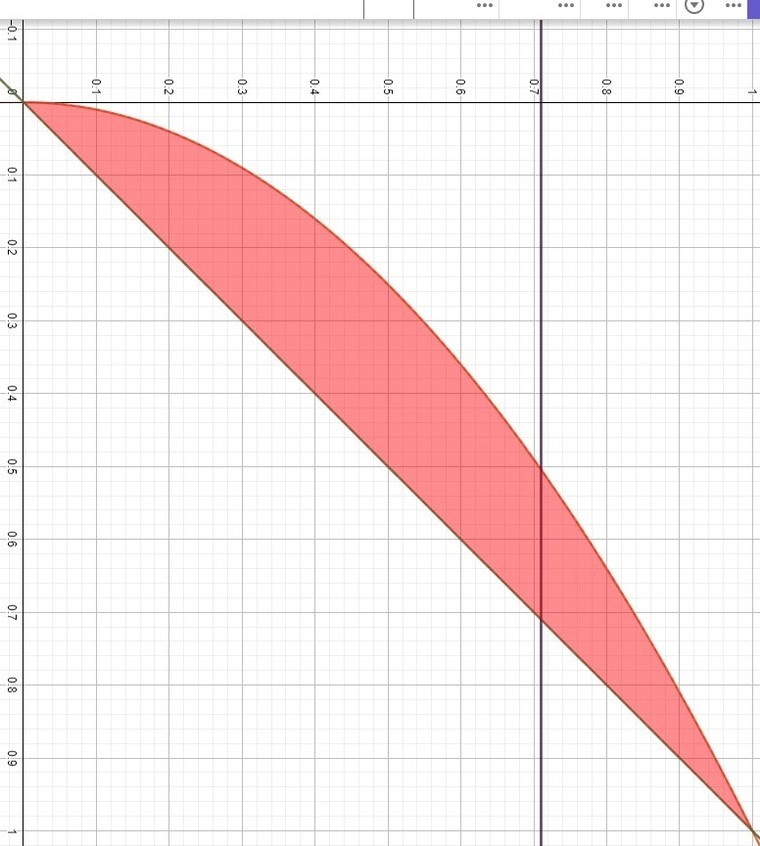
[You can see from the picture and ignore the co-ordinate marking]
inverse of s q r t ( x ) = x 2 and its obvious that the inverse is lifted by a factor of 1 from center and its facing downwards now so we end up with − x 2 + 1
inverse of straight line is same except this time we have lift of +1 and - slope so we end up with − x + 1
integral of this will be same as the actual function=1/6
we can find the point where integral sum =1/12 which is half of the area as following
− x 3 / 3 + x − ( − x 2 / 2 + x ) = 1 / 1 2 (This function is the difference of the antiderivatives of corresponding functions ,so it represents the
area since lower limit is 0)
we will get 3 distinct points as solution but only 0 . 5 lies in the interval [0,1]