That's No Sun
Suppose we combine a unit circle and a square of the same area, as shown above, such that their centroids lie on the same point. What is the area of the non-overlapping white region?
If your answer is of the following form A arctan ( π − C π ( B − π ) ) − D π ( E − π ) , where A , B , C , D , and E are positive integers, evaluate A + B + C + D + E .
The answer is 16.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
A=8, B=4, C=0, D=2 and E=4 would have also worked.
Log in to reply
That's right, because of the following trigonometric identity
2 A r c T a n ( b b ( 2 a − b ) ) = A r c T a n ( b − a b ( 2 a − b ) )
provided that 2 a > b > a
Log in to reply
That's a surprisingly nice identity!
Log in to reply
@Calvin Lin – Yes, it is! It's actually simple to derive this by using the sum of arctan . Good thing that @Michael Mendrin provided the necessary bounds for the identity. :)
Log in to reply
@Michael Huang – I prefer a geometrical approach, shown in the graphic below which should be self-explanatory, using a semicircle to construct a geometric mean. Note that the exterior angle of an isosceles triangle is twice that of one of base angles.
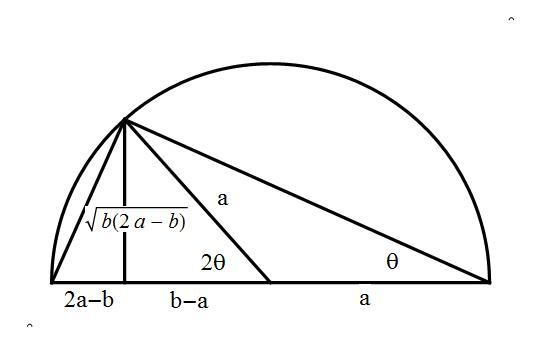
Log in to reply
@Michael Mendrin – Nice! This could be the part of the next solution! XD
Thanks. I see that this problem has been edited. Those who previously answered 4.24 has been marked correct.
In future, if you spot any errors with a problem, you can “report” it by selecting "report problem" in the menu. This will notify the problem creator (and eventually staff) who can fix the issues.
Your diagram and explanation is very clear!:) Although, the length α β should have two lines across it (not that it really matters).
As a result, I also got A=8 B=4 C=0 D=2 E=4. There are no restrictions on variables in the task condition. The question remains the same: Is it necessary to make trigonometric transformations?
FYI I updated the question to ask for A + B + C + D + E directly, as that avoids having another hoop for people to jump through.
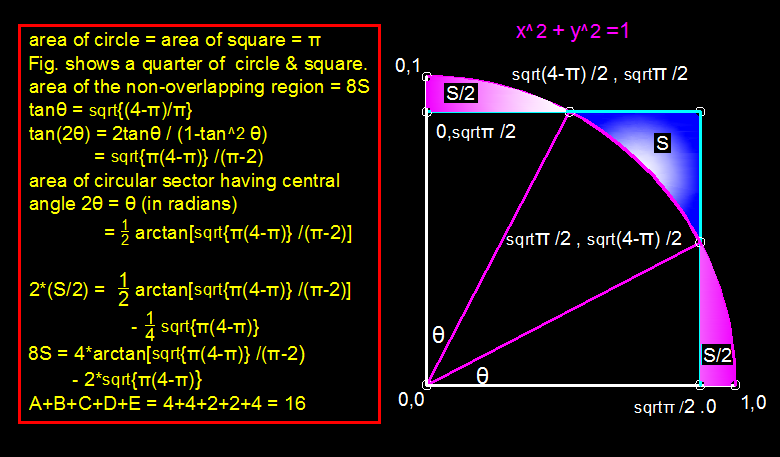
Section I. Beginning Step
Since both square and unit circle have the same areas, A square s 2 s = A circle = π = π where s denotes the length of the square.
Since the centroids of both shapes lie on the same point, we can show that (1) 4 white regions of the square extend outside of the circle, and that (2) the combined shape is symmetric with respect to the 4 lines. Splitting the square into 4 congruent squares, we can see that the diagonal length of the subsquare is 2 2 π > 1 . In this case, since these square share the common point, the square is not fully bounded by the circle.
Section II. Area Computation
From the second diagram, observe that
where the angle unit is in radians. The next steps are to determine and use the areas of the colored regions for the area difference.
Section II.1. Area of Concave Shape
Since Δ δ α β is the right triangle, Pythagorean Theorem shows that ∣ δ β ∣ = ∣ δ α ∣ 2 − ∣ α β ∣ 2 = 1 − 4 π = 4 4 − π = 2 1 4 − π Since there are two congruent triangles in the subsquare with these common side lengths, A triangles 1 = 2 ⋅ 2 1 ( 2 π ) ( 2 4 − π ) = 4 1 π ( 4 − π )
which is equivalent to determining the area of the rectangle of two combined triangles. For the arc sector, by trigonometry, since cos ( ∠ δ α β ) ∠ δ α β = 2 π = arccos ( 2 π ) and the subsquare is symmetric with respect to its diagonal, we have ∠ γ α δ = 2 π − 2 ∠ δ α β = 2 π − 2 arccos ( 2 π ) So the area of the sector is A sect 1 = 2 ∠ γ α δ which I chose to evaluate later. Therefore, the area of the white region is A net 1 = A subsquare − A triangles 1 − A sect 1 = 4 π − 4 1 π ( 4 − π ) − 2 ∠ γ α δ
Section II.2. Area of Convex Shape
Focus on arc sector μ γ α . Because it also shares the common triangles with the subsquare, A triangles 2 = 4 1 π ( 4 − π ) Then, since ∠ μ α γ = 2 ∠ δ α β , A sect 2 = ∠ δ α β Therefore, A net 2 = A sect 2 − A triangles 2 = ∠ δ α β − 4 1 π ( 4 − π )
Section III. Final Step
So A white = 4 A net 1 + 4 A net 2 = 8 arccos ( 2 π ) − 2 π ( 4 − π ) Since arccos ( 2 π ) = arctan ( π 4 − π ) and 2 arctan ( α ) = arctan ( 1 − α 2 2 α ) where α = π 4 − π , the resulting area is 8 arctan ( π 4 − π ) − 2 π ( 4 − π ) = 4 ( 2 arctan ( π 4 − π ) ) − 2 π ( 4 − π ) = 4 arctan ( π − 2 π ( 4 − π ) ) − 2 π ( 4 − π ) where A + B + C + D + E = 4 + 4 + 2 + 2 + 4 = 1 6