That's one huge yo-yo!

Classical Mechanics Level 5

In an alien planet, an alien wants to play yo-yo. The gigantic yo-yo consists of two solid disks, each of mass $15 kg$ and radius $5 m$ , connected by a central spindle of radius $2 m$ and negligible mass. A string is coiled around the central spindle. The yo-yo then is placed upright on a rough flat surface and the string is pulled gently with a tension of $10 N$ at an angle $30^\circ$ to the horizontal. The pull is gentle enough to ensure that that yo-yo does not slip nor lifts off the ground.

The acceleration of the center of mass of the yo-yo can be expressed in the form $\dfrac{a\sqrt{b}-c}{d}$ . Where $a$ is as large as possible, $gcd(a,d)=5$ and $gcd(c,d)$ =1. What is the value of $a+b+c+d$ ?

Assume that the only difference between the planet and earth is the size of the inhabitants and the planets, nothing else.

The answer is 57.

3 solutions

Steven Zheng
Aug 19, 2014

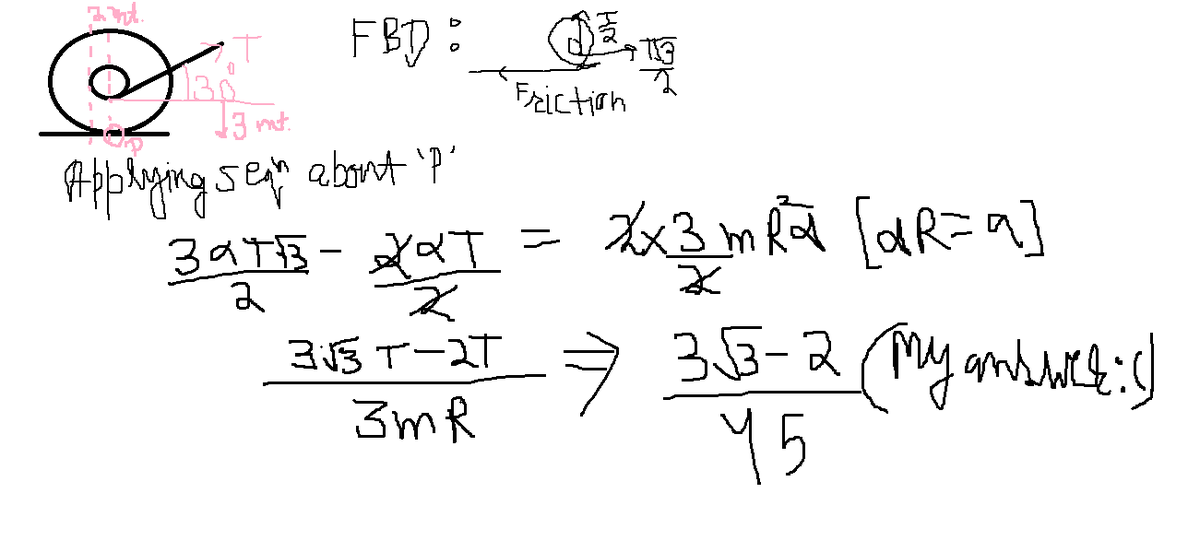
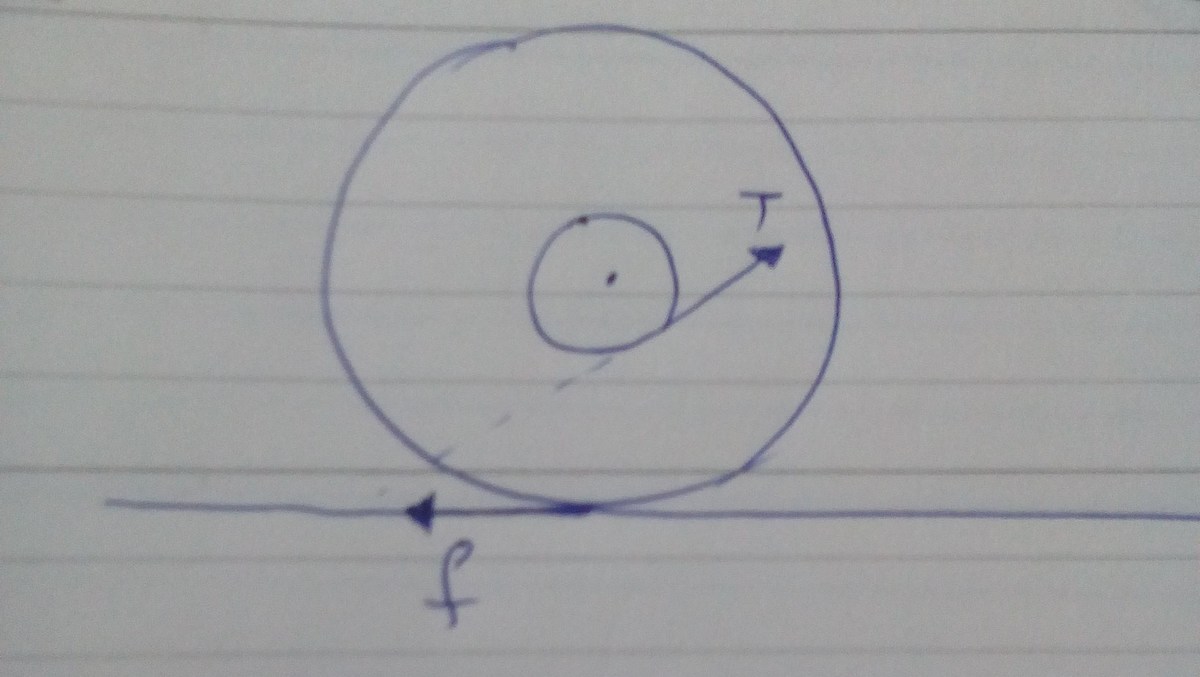
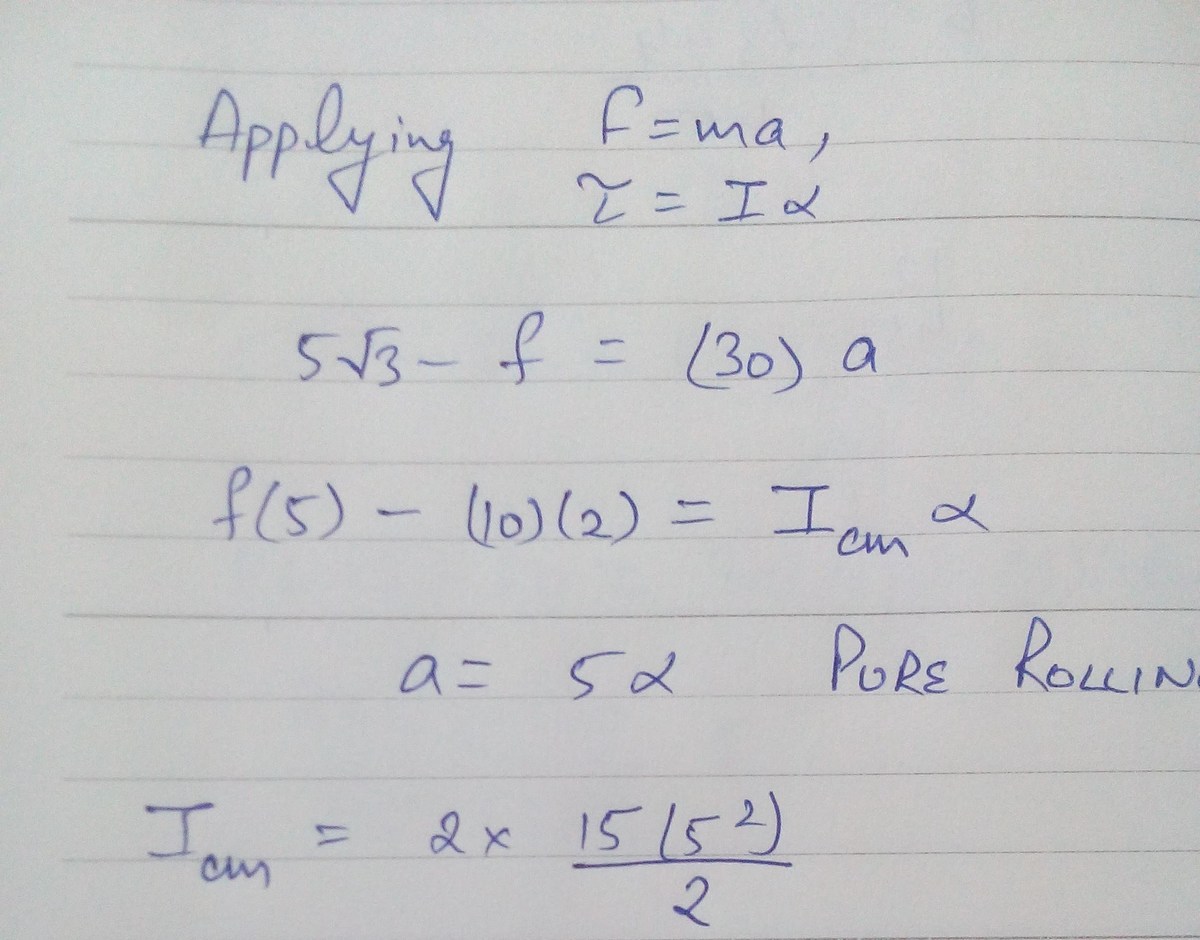
This problem is quite tricky because you have to account for the rotational and linear motions. I've solved a simpler problem involving pulling a hockey puck (only one radius and disk).

For the rotational motion, we begin with the torque of the system. If we were to draw a free-body diagram, the large radius is tangential to the force of friction $D$ (D for dissipative) while the small radius is tangential to the tension of the string. Since we have two solid disks, the moment of inertia $I$ is $M{R}^{2}.$ Hence the total torque can be summed up as: $RD-rT = M{R}^{2}\alpha =MRa$ or $D-\frac{rT}{R} = Ma.$

For the linear motion, we derive the net force $Tcos(30) - D = 2Ma.$

Substituting the value of Ma from the linear motion to the rotational motion $D-\frac{rT}{R}=\frac{Tcos(30) - D}{2}$

which can be rearranged as: $D=\frac{T(cos(30)+\frac{2r}{R})}{3}.$

Now we substitute this equation for D, and isolate the acceleration we arrive at the final equation: $a = \frac{T}{3M} \left(cos(30) -\frac{r}{R}\right).$

I also noticed an error with the question. The gcd(a,d) = 5.

plz help sir, also sir @Josh Silverman

hiroto kun - 4 years, 3 months ago

Hi @hiroto kun , it's hard to read your diagram. Can you list the main steps you're confused about?

Josh Silverman Staff - 4 years, 3 months ago

i'm confused about " y my method is wrong" ?

hiroto kun - 4 years, 3 months ago

@Hiroto Kun – OK, what I'm saying is I can't read your diagram partly because of handwriting, partly because you skip a lot of steps and put in specific numbers. If you can summarize your steps I can help out.

Josh Silverman Staff - 4 years, 3 months ago

@Josh Silverman – first i made free body diagram .resolved tension in 2 components . then applied torque equation . wrote acceleration = angular acceleration *Radius , the answer i got is mentioned above . thnx sir for seeing to it :). you're awesome .

hiroto kun - 4 years, 3 months ago

Oops, sorry! (I'll just follow what you say for now, I'll check it if I feel better)

Sean Ty - 6 years, 9 months ago

The sign of the answer expression shall be positive. It shall be:- $\dfrac{a\sqrt{b}+c}{d}$