That's quite a few resistances
This is a great rhombicosidodecahedron :
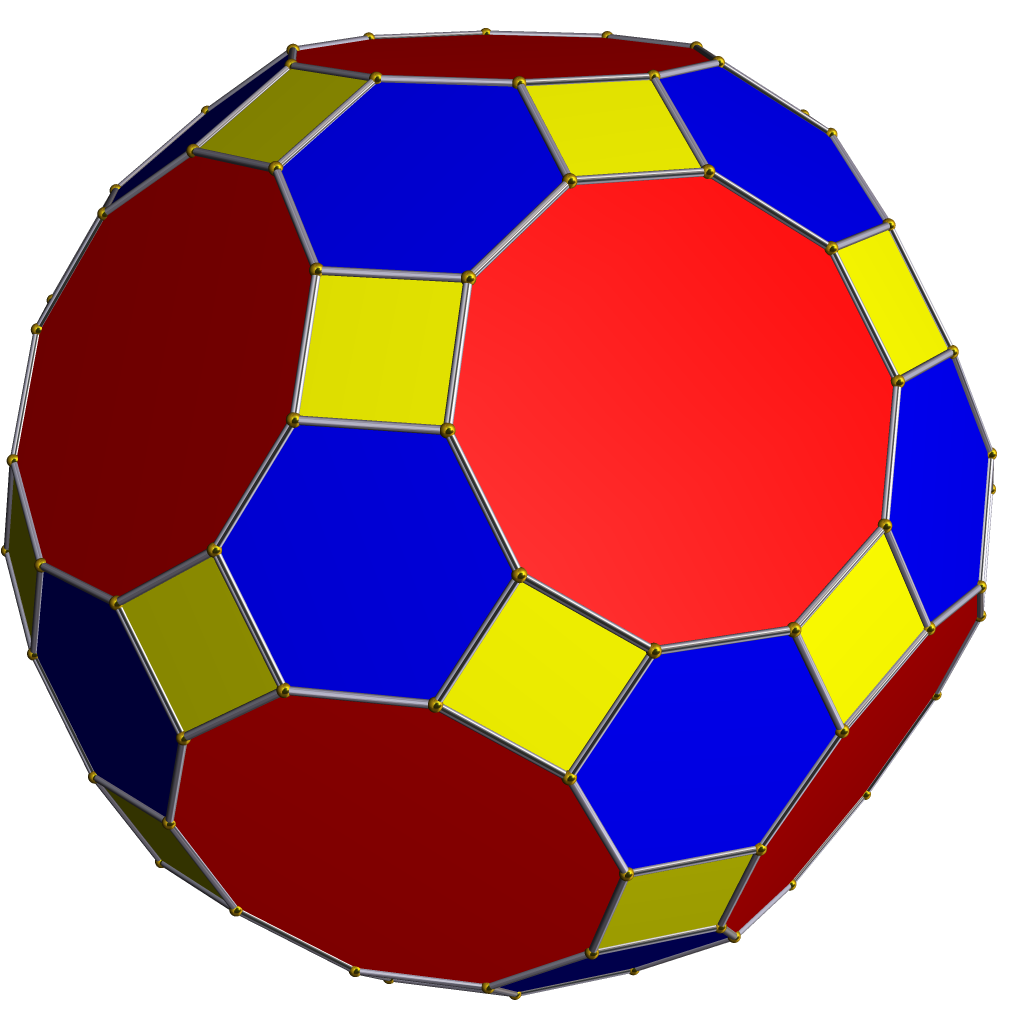 Great Rhombicosidodecahedron
Great Rhombicosidodecahedron
If the faces are non-conducting, and each of the edges has a resistance of 1 0 0 Ω , what is the highest effective resistance (in ohms) you can obtain between any two vertices?
Round your answer to the nearest integer if necessary.
Image credit: commons.wikimedia.org
The answer is 203.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
This Mathworld page refers to a paper by Babic et al, which gives an explicit formula for all the effective resistances of a connected graph. The Mathworld page then helpfully gives all the resistances for the Platonic and Archimedean solids! For the great rhombicosidodecahedron, the largest possible resistance is 1 0 0 × 2 6 7 5 1 4 3 8 0 5 4 2 4 6 6 0 5 0 = 1 0 0 × 2 1 1 1 4 4 2 8 1 5 ≈ 2 0 3
Really? We have to solve 118 linear equations? This problem should be a Level 8 problem then...
Log in to reply
Yeah... Not one of my more elegant solutions... :/
Was hoping someone might post a much more clever solution taking advantage of all the symmetry that this solid has...
Log in to reply
How did you solve these 118 equations in the first place?
Log in to reply
@Pi Han Goh – Of course, I didn't solve these by hand... Are you, like, a crazy person? ;-)
The compute intensive, but somewhat uninteresting solution, of course, is the brute force method of picking two opposite vertices A and Z, applying a voltage of 1V to A, and grounding Z, (Note, this doesn't imply we only have 26, vertices, you'll need to come up with creative names for the other 94 nodes :) ) and solving Kirchoff's equations at each of the other 118 nodes.
I have labeled a few nodes here for reference here:
This gives you the following set of 118 linear equations:
⋮
etc.
where V n = The voltage on node n
Finally, once we solve the above set of linear equations, we end up with 118 voltages. Lets consider the three on the nodes next to Z and call them W, X, and Y.
The current from A to Z is the sum of the currents from W to Z, X to Z, and Y to Z, which will be V W / 1 0 0 , V X / 1 0 0 and V Y / 1 0 0 (since we have 100 ohm resistors on all edges).
So, R e q = 1 0 0 ∗ ( V W + V X + V Y )
Once you solve the above set of linear equations, you get:
V W + V X + V Y = 4 2 8 1 5 / 2 1 1 1 4 ≈ 2 . 0 3
So, R e q = 2 0 3 .
As I said, not pretty, but it gets the job done...
If anyone has a more elegant way, I'd love to see it! :-)