The 35 years ago
1 9 8 1 + 1 9 8 1 − 1 9 8 1 + 1 9 8 1 − 1 9 8 1 + ⋯ = ?
The answer is 45.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
I keep asking this question: How do you know that it converges?
Log in to reply
And its highly probable that you will not get a answer here too :-)
Log in to reply
Why don't you defy the odds?
Or, better yet, prove the convergence of this one . Good luck with that! ;)
Log in to reply
@Otto Bretscher – Oh... Need to study for that.... Convergence is something which I came to know on briliant and I really need to work on that concept real hard... And still this question can be approached by:
x = 1 9 8 1 + 1 9 8 1 − 1 9 8 1 + 1 9 8 1 − ⋯ = 1 9 8 1 + y y = 1 9 8 1 − 1 9 8 1 + 1 9 8 1 − 1 9 8 1 + ⋯ = 1 9 8 1 − x Then squaring , manipulating and subtracting will do the job but I knew I would end up having convergence issues.. :-)
Log in to reply
@Rishabh Jain – We can consider the iteration function f ( x ) = 1 9 8 1 + 1 9 8 1 − x with the seed a 0 = 1 9 8 1 ≈ 4 4 . 5 . This is a very strong contraction, with ∣ f ′ ( x ) ∣ < 0 . 0 0 1 on [ 4 4 , 4 6 ] , so that the nested radical will converge to 45 very quickly.
@Rishabh Jain – The best way!!!
Let be A. If we square A. We get 1981 +
be A. If we square A. We get 1981 +
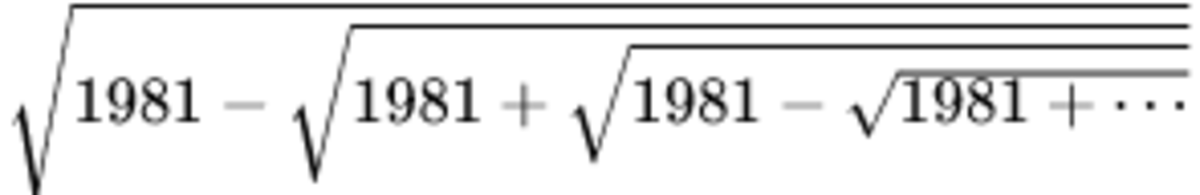 . However,
. However,
 is also A. Hence A^2 = 1981 + (1981-A)^(1/2), A=45.
is also A. Hence A^2 = 1981 + (1981-A)^(1/2), A=45.