The answer is also not 1200, nor 900

Imgur

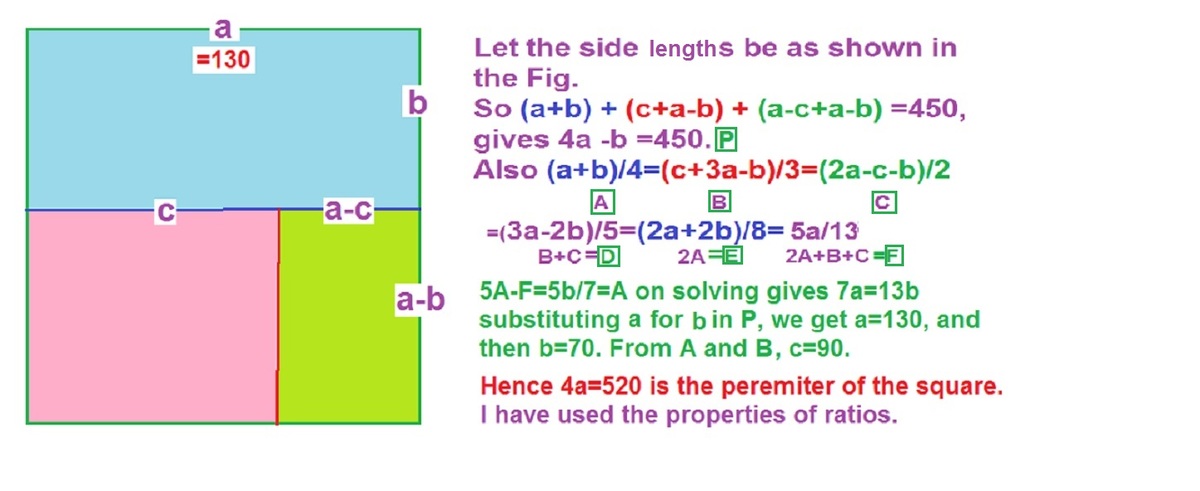
Since the perimeters add up to 900 and are in the ratio 2:3:4, they must be 200, 300 & 400. Marking the semi-perimeters in the rectangles as shown, and assuming x to be the side of the square, we can go clockwise around it and write expressions for the sides of the rectangles as: [1] = 200 - x, [2] = 2x - 200, [3] = 300 - 2x, [4] = 3x - 300, [5] = 450 - 3x, [6] = 4x - 450

But lengths [6] and [1] are equal! (opposite sides of the top rectangle) giving x = 130 and the desired perimeter = 520

Rectangle having the longest length is made one side of the square so that the square has the maximum perimeter. The other two makes no difference, which is on the left and which on the right.

The total of the 3 perimeters is 900. Therefore 2x + 3x + 4x = 900

x=100, the 3 perimeters are 200, 300, and 400. The only valid solutions occur if the purple rectangle is the largest one and the 2nd largest, namely 400 and 300.

Let x = the side of the square, and the length of the purple rectangle, y = the width of the purple rectangle, and z = width of one of the other rectangles, the largest perimeter of the square can be found to be 520.