Troublesome Cylinder!
A cylinder is rolling with speed v 0 = ω 0 R over a frictionless horizontal surface toward the wall, as in the figure below. The coefficient of friction between the wall and the cylinder is μ = 4 1 .
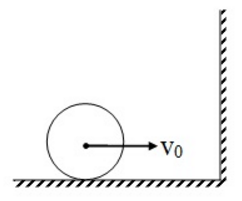
If the collision between the cylinder and the wall is completely inelastic, find the kinetic energy of the cylinder after the collision.
Given that this kinetic energy can be expressed as b a m v 0 2 , where a and b are coprime positive integers, what is a + b ? After done with this you may also want to to do this
The answer is 35.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
I don't see why if the collision with the wall were perfectly elastic, instead of inelastic, then the angular velocity of the cylinder would be turned to 0 by the collision. can you explain it please.
Log in to reply
I guess I overstated the case.
Suppose we understand "perfectly elastic" to mean "energy-conserving". Suppose that the cylinder has horizontal velocity v x away from the wall, and vertical velocity v y , and also has angular velocity ω . Conservation of angular momentum (about the point of contact of the cylinder with the wall) tells us that r ω + 2 v y = v 0 while, assuming conservation of energy, we deduce that r 2 ω 2 + 2 v x 2 + 2 v y 2 = 3 v 0 2 Since the impulsive normal reaction is four times larger than the impulsive friction force, we also deduce that x v + v 0 = 4 v y Putting these three equations together we deduce that ( r ω − v 0 ) ( 1 9 r ω + v 0 ) = 0 and hence (either r ω = v 0 , which is what happens if no collision occurs, or) r ω = − 1 9 1 v 0 , and so the cylinder has, in fact, a nonzero angular velocity after the collision.
If we take "perfectly elastic" to mean "the cylinder moves away from the wall with the same speed as it approached the wall (so the coefficient of restitution is 1 ", then we would have v x = v 0 and v y = 2 1 v 0 , which would imply that ω = 0 . But then energy is not conserved.
Elastic collisions are more complicated when the colliding objects are no longer point particles!
Log in to reply
thank you Mark for your answer. I always read you and enjoy your style of considering all the details.
But once again at the end I have a new point for which I am not OK with you. here is it: "If we take "perfectly elastic" to mean "the cylinder moves away from the wall with the same speed as it approached the wall (so the coefficient of restitution is ", then we would have Vx=V0 and Vy=1/2*V0 , which would imply that . But then energy is not conserved."
correct me if I'm wrong, in this last case we will not have w=0. and the energy will be conserved. All what we have to do is taking sqr(Vx)+sqr(Vy)=sqr(V0) then calculate w for witch the energy is conserved.
Log in to reply
@Mr X – No, because angular momentum about the point of impact will be conserved. If v y = 2 1 v 0 , then we must have ω = 0 , since r ω + 2 v y = v 0 . Energy is not conserved. We do not have the luxury of choosing the value of ω that we want.
Log in to reply
@Mark Hennings – plz try my other problem too !!
@Mark Hennings – One last question : is it possible to have a perfectly elastic collision on a surface with friction?
Log in to reply
@Mr X – If no slipping occurs during the collision (and the collision is thought of as instantaneous, so there is no time for such motion), then the friction forces will do no work, and so should not affect conservation of energy.
https://brilliant.org/problems/another-troublesome-cylinder/ try it's next part too!
464 views (100%) 174 attempts (38%) 16 solvers (3%) yet level 4 :'( @Josh Silverman
Shubham's solution with a little more detail.
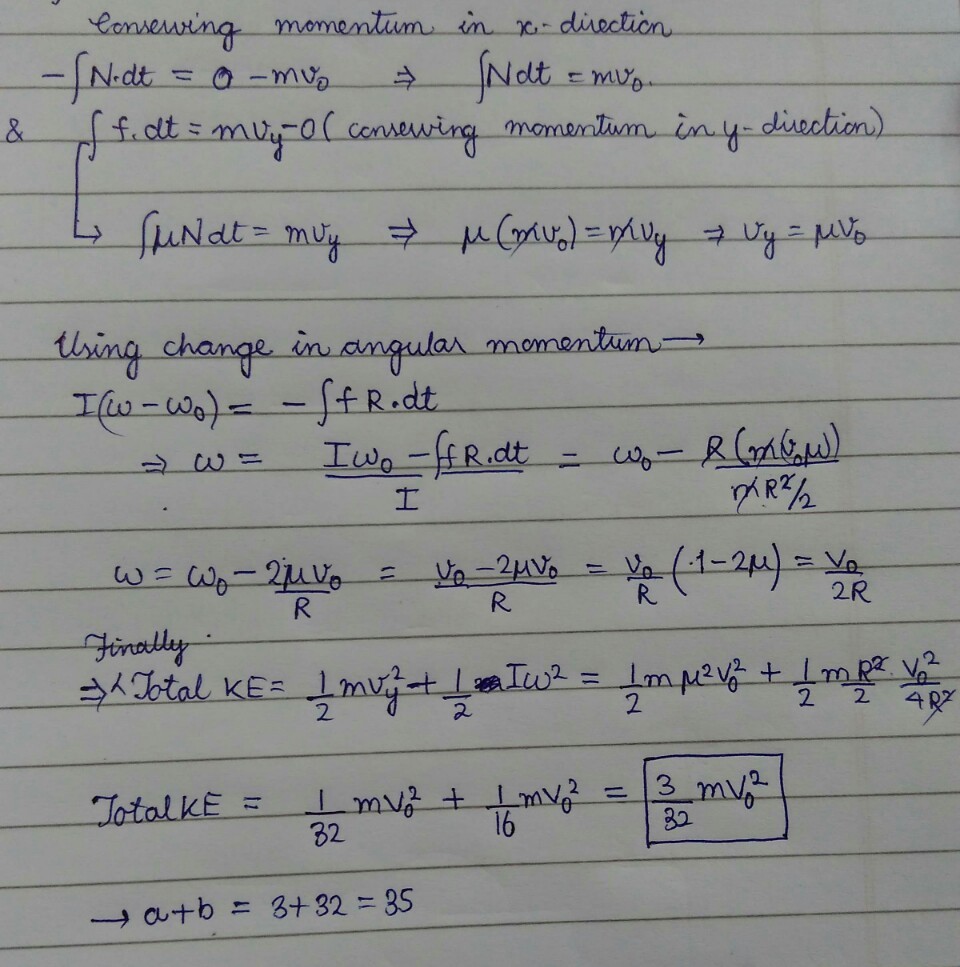
Yes, I forgot to mention that this is just a extension of your solution, for those who are finding it difficult.
Log in to reply
I don't know, but I saw your name missing from the conversation list, so I just asked about it, nothing else
how is your advance prep going /( on 14th nov. ?? )
Log in to reply
Well, I was preparing for KVPY along with advance, but fairly speaking, my school is just after me on practicals, making it difficult to study
Since the cylinder is lifted up the ground after the instant of collision,shouldnt the weight of it also be taken into account?? It's gaining potential energy and it doesnt come for free😀 The friction force should do work again st gravity to impart it vertically velocity,shouldnt it!!
Log in to reply
Since friction is a non conservative force and in inelastic collisions kinetic energy is not conserved, you cannot apply work energy theorem here, even if you calculate the work done by friction.
Log in to reply
Yes absolutely,thers no denying that,but then where did the force of gravity disappear,since the cylinder has got vertical velocity it must surely be off ground,so doesn't gravity resist this motion??
Log in to reply
@Chirag Shyamsundar – Normal reaction acts as a catalyst in this scenario,helping cylinder to lift of without doing any work.
Same is the case a football collides with a staircase and rolls abt the edge of stair.
@Mark Hennings can you please provide some insight to us?
Log in to reply
@Harsh Shrivastava – While the cylinder is in contact with the floor, the normal reaction from the floor on the cylinder equals the force of gravity, so their effects cancel out. Once the cylinder lifts off, after the collision, the force of gravity will affect the future motion.
During collisions, we are primarily interested in impulses. These are the effect of very large ("infinite") forces F acting over very small ("zero") time in such a way that the integral of F with respect to time (the impulse) is finite. The impulsive version of Newton's equations are that:
- an impulse produces an ("instantaneous") change of momentum,
- an impulsive torque produces an ("instantaneous") change in angular momentum.
During the collision, the normal reaction with the wall, and consequently the friction force with the wall, are impulsive in nature. The normal reaction with the floor and the force of gravity are not. These are both equal to m g , and a finite force integrated over a very small ("zero") time interval will provide a negligible ("zero") impulse. Thus the only impulses we need to consider are those given by the normal reaction and friction with the wall, since these are the only nonzero ones.
https://brilliant.org/problems/another-troublesome-cylinder/ try it tooo!
Initially i didnt thought of taking the vertical velocity gained by the cylinder.
Log in to reply
Same here @Md Zuhair
Log in to reply
accha sun.. if it was not a perfectly inelastic collision.. phir bhi hota kya vertical velocity? Like just after collision there will be no contact with wall.. then it shouldnt have that na?
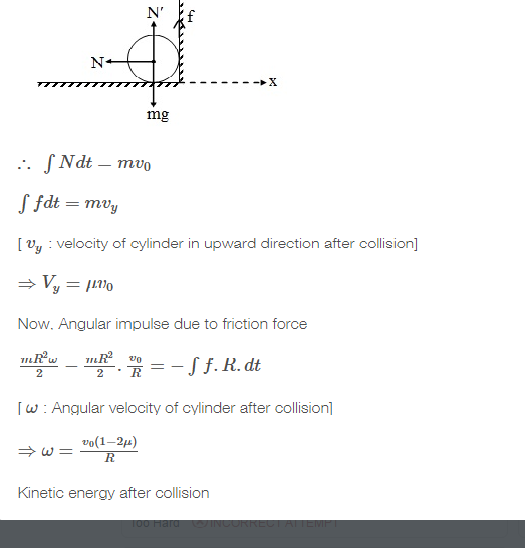 after you do it all, you will get the answer as
a
=3 and
b
=32.
after you do it all, you will get the answer as
a
=3 and
b
=32.
The solution is not clear at all
Log in to reply
why ? i think i have give sufficient information sir !
The solution is very poor.Please be a bit more detailed....
Log in to reply
i think i have give sufficient information , i will be able to help if you tell what's not clear, right? also, plz make sure you have covered the basics of rigid body dynamics because if you had your basics clear, the terminologies and the solution would be automatically be crystal clear to you . cheers :)
hope it's clear , cheers!
Log in to reply
Nice question. Also, have you stopped using slack?
Log in to reply
yep, deleted (deactivated) my account there
upvote and like my sol. so that this problem reaches to more people!
Since the collision with the wall is perfectly inelastic, the wall exerts a normal impulse of m v 0 on the cylinder, and hence a frictional impulse of 4 1 m v 0 is exerted upwards on the cylinder. After the collision, the cylinder has velocity ( 0 , 4 1 v 0 ) . The frictional impulse reduces the angular velocity of the cylinder by Δ ω , where 2 1 m r 2 Δ ω = 4 1 m v 0 r and hence Δ ω = 2 r v 0 , so that the angular velocity of the cylinder after the collision is r v 0 − 2 r v 0 = 2 r v 0 . Thus the kinetic energy of the cylinder after the collision is 2 1 m ( 4 1 v 0 ) 2 + 2 1 × 2 1 m r 2 ( 2 r v 0 ) 2 = 3 2 3 m v 0 2 making the answer 3 5 .