The ant Honey
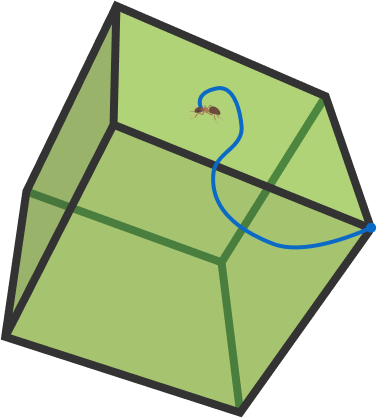
An ant named Honey is kept outside a solid cube on a leash, which extends to twice the side length of the cube.
The leash can be attached
- on the center of a face , or
- on the midpoint of an edge , or
- on a vertex .
Which choice gives Honey the greatest area to roam?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
In your middle figure, for the midpoint of an edge, the red areas suggests those parts that cannot be reached. But actually, most of the red areas marked can be reached. Same thing with the right figure, for the vertex.
Log in to reply
I'm aware of the fact the second and third image have flaws since some of the red area can get reached by approaching it from a different angle. The red area in the second figure gets reduced by about 66% and the red area in the third figure by about 46% when those other angles get considered as well. While writing the solution, I skipped those detail to keep the explanation simple.
Log in to reply
What you could have done is to show how some of the red parts can be reached by other means, which can be done by adding some more circles in the right places. But if you look at the second figure, considerably more than 66% of the red area is reduced by "other means", which is Jeremy's point. Very little cannot be reached from the midpoint of an edge, tiny slivers pointed out in the second figure where it says "here"
But since the problem only allows a single choice, then picking the center of face is all that matters. It would have been different if multiple choices were allowed, because then we'd have to conclusively show that not all of the surface of the cube can be reached from the midpoint of an edge.
that assumes that the ant is not permitted to travel over two faces... the area that is able to be traveled is only limited by the length of the leash... A= leash_length^2 * pi
The trouble with this solution as shown is that it doens't show all the ways the ant can try to reach the point most opposite from him. You are overestimating the areas of the unreachable red parts. With the middle figure for the midpoint of an edge, how do you show that the ant cannot reach any of the parts marked red in it? Same thing witrh the right figure for the vertex.
Log in to reply
I'm aware of the fact the second and third image have flaws since some of the red area can get reached by approaching it from a different angle. The red area in the second figure gets reduced by about 66% and the red area in the third figure by about 46% when those other angles get considered as well. While writing the solution, I skipped those detail to keep the explanation simple.
Area is area no matter where on the cube it is which is determined by the length of the string, should this have been worded the furthest on as many side's as possible?
The (3) alternate positions of the "bottom" face of the cube could have been drawn in dotted lines at the edges of the (3) other side faces (up , left & down). Then, the bottom face can be swept clean from different arcs which intersect at the mid-point of the bottom..
Wow. You're smart.
It seems so, but actually it is not as describe. When attached to the middle point of the cube, still, some part cannot be reached, since the line is limited by the edge. Try to imagine that.
But the question was what maximized the area she could reach. NOT the area on the surface of the cube she could reach.
Log in to reply
Err... there's area the ant can reach that's outside the surface of the cube?
Very helpfull to add an image. The image would be more intuitive though if you would split the opposite face (the face at the far right in the 2D cross layout) into four triangles and attach each triangle to a side face, resulting in a symmetrical 2D layout. Then the complete 2D layout falls inside a circle with radius 2.
Log in to reply
Yes, I suppose that would indeed make it more clear than what I did.
This is wonderful!!
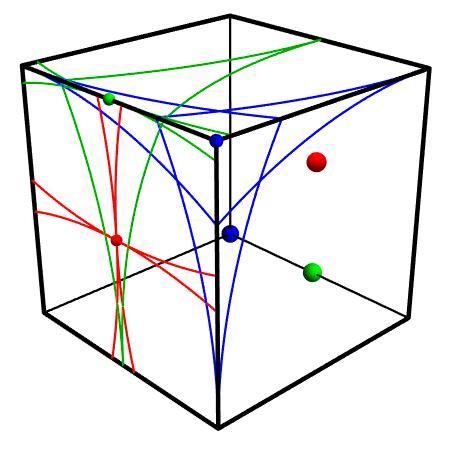
The blue is on a vertex, with its opposite point also on a vertex.
The geen is on the midpoint of an edge, with its opposite point also on a midoint of an edge.
The red is on the center of a fact, with its opposite point also on a center of a face.
The blue is the worst, missing much of the area near the opposite vertex.
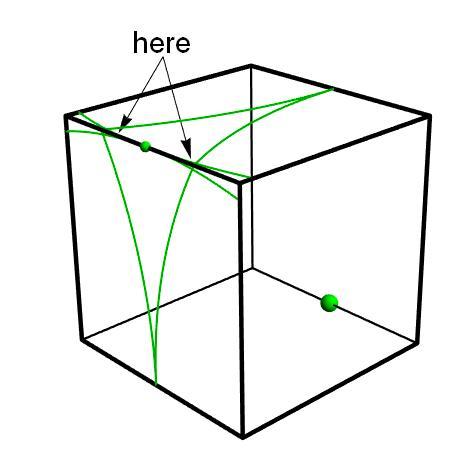
The green nearly covers all, but misses tiny areas near its opposite midpoint (see "here")
The red covers all.
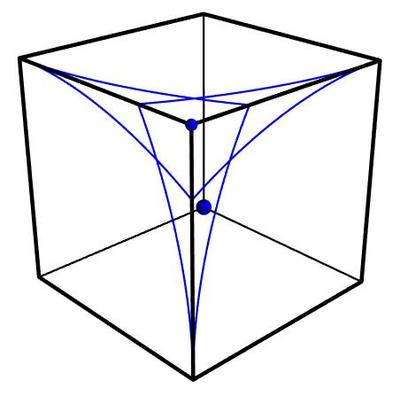
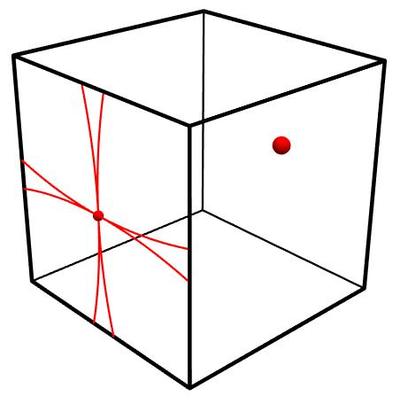
Ronin says:
"I don't think you need all of that for a proof. Your example point of ( 0 . 6 , 1 , 1 ) is a distance farther than 2 away when traversing two faces, and when traversing three faces, well: 0 . 4 2 + x 2 + 0 . 5 2 + y 2 + ( 1 − x ) 2 + ( 1 − y ) 2 − 2 achieves a minimum, rounded down, of 0 . 0 5 . So I think providing one such point is sufficeint proof, that there exist points out of reach of the leash."
See his comments below.
Those pictures are wonderful.
Log in to reply
Thanks. I just wanted to see how it looks in 3 dimensions.
Nice solution.
I thought the leash could go off the interior surface...
Log in to reply
I'm not sure what you mean by that. The cube is solid, the leash can only wrap around on its surface.
Log in to reply
I just now realized the problem says the ant was kept on the outside of the cube, my bad.
As regards the blue (vertex) cube, it seems to me that the ant can reach slightly more than that. If the ant first goes a diagonal (and not along an edge), it will use square root of 2 of its leash. It can then go another (1-sqare root of 2) along the edge towards the opposite vertex. I believe the non-reachable surface is a quarter of a circle from the opposite vertex, on each of the 3 sides.
Beautiful solution!
If I did my geometry right, the green curves are omitting a path that allows the unreachable area to get ever so slightly smaller. Take the large green boundary curve on the right half of the front face of the cube: that curve is generated when the ant starts out going up slightly along the back right side and traveling around the side of the cube, but the ant can get slightly farther if he travels first along the underside, then up to the right front side and over to the left front.
How did you create these pictures?
Log in to reply
I use Mathematica for such 3D illustrations, but it still requires combining separate images.
Beautiful images.
(EDIT: The following from the original comment is wrong, but I'm not sure how to do strikethrough here: But the farthest point from a midpoint of an edge is not the diagonally adjacent edge midpoint, rather it's one of the vertices of that diagonally adjacent edge.)
Log in to reply
Good point, I should have clarified by saying, "Opposite point across the cube. Let me fix that.
Log in to reply
Upon further reflection, I think the answer to this question is wrong. Namely, both the center face and edge midpoint pivots cover the entire cube. I thought those vertices of the diagonally adjacent edge were the farthest points at 1 7 d / 2 , where d is the edge length. That would explain why in your figure they cannot be covered. However, you are right in that the diagonally adjacent edge midpoint is farthest at 2 d . From your larger green point, and our perspective, move right d / 2 to the edge and up d / 3 on the same face as the larger green point. Then coming across that nearest right face, you will go up another 2 d / 3 and over left by d . So, that makes 1 / 9 + 1 / 4 d + 1 + 4 / 9 d = 1 3 d / 2 < 2 d . Ergo those vertices which are missed in your figure can in fact be covered.
Log in to reply
@A Former Brilliant Member – Ronin, those vertices you are talking about ARE within reach from the midpoint of that edge. As both Jeremy and I have tried to explain, only tiny areas (shown by arrows from "here") cannot be reached. Those vertices that you are talking about cannot be reached by one way but can be in another.
Maybe I should go draw in some more lines in that figure?
Log in to reply
@Michael Mendrin – Maybe? But then the proof is incomplete because "here" is ill-defined. You then mean points that are close to the diagonally adjacent edge midpoint, right? Will some of those points be greater than 2 d away, because if not then there will exist a way to get there.
Log in to reply
@A Former Brilliant Member – Let's assume that the cube has unit sides, so that the coordinate of the 1st midpoint is ( 2 1 , 0 , 0 ) , and the 2nd ( 2 1 , 1 , 1 ) . I'll pick a point ( 0 . 6 , 1 , 1 ) . Can it be reached by travelling no further than 2 from the 1st midpoint? It looks like to me that 3 faces will have to be travelled over, since we know that 2 faces won't work.
Log in to reply
@Michael Mendrin – Intuitively I think your figure is right. After all I also answered the face center for the problem explicitly because I also visualized the semi-circle sweeping shown in your figure. But now for a proper proof, I think we need to show that the farthest point away from an edge midpoint, when constrained to the surface, is greater than 2 d .
Your example here seems like it should be farther yes, but then upon first glance so does the point ( 1 , 1 , 1 ) .
Log in to reply
@A Former Brilliant Member – To be fair, I did not offer a "proof" nor have I included all the boundary arcs---only just enough to show that tiny green area that cannot be reached. A full proof consists of drawing a lot of circles in a lattice, carefully marking where the 2nd midpoint is represented on that lattice.
All the vertices and midpoints of edges can be reached from the 1st midpoint.
Log in to reply
@Michael Mendrin – I don't think you need all of that for a proof. Your example point of ( 0 . 6 , 1 , 1 ) is a distance farther than 2 away when traversing two faces, and when traversing three faces, well: 0 . 4 2 + x 2 + 0 . 5 2 + y 2 + ( 1 − x ) 2 + ( 1 − y ) 2 − 2 achieves a minimum, rounded down, of 0 . 0 5 . So I think providing one such point is sufficeint proof, that there exist points out of reach of the leash.
Log in to reply
@A Former Brilliant Member – Well, thanks for providing one for me. Is it okay if I quoted you in my solution so that others can see?
Only if she is attached to the center of a face can Honey reach anywhere on the cube.
If she is leashed to a vertex, she can't reach the opposite vertex.
If she is leashed to the center of an edge, she can't reach the entire opposite edge.
Traditionally, we call the ant Brilli because it is Brilli-ant.
Log in to reply
I made my own pun.
Here are few of my food-for-thoughts problems that are related to the one you asked: (1) , (2)
Log in to reply
I’m still looking for a pet fly. That will be my version of that second problem.
your assumption is wrong though. even when connected to the center of the face she can not reach anywhere on the cube.
Log in to reply
She can. She can reach the center of the opposite face from four different directions. This can best be seen in Michael Mendrin's solution.
Log in to reply
I agree that she can reach center of the opposite side. But only going around the center of the edges. She could not reach the center by going along the vertices/diagonal, as the rope would be too short. Just wanted to clarify that
Log in to reply
@Arvid Schneider – I though the same thing Arvid! Assume the cube has side length "a". If Honey tried to go along the the vertices/diagnonals, the distance to the center of the opposite face would be (Sqr root of 2)x(a)+(a) which is LONGER than 2a (the length of her leash). So there is a certain area on the opposite face that she could not reach.
The ant can reach anywhere on the cube when leashed to the center of a face.
The problem did not state that the surface of the cube was the only surface to be considered
The diagonal of a cube is less than twice the length of the cube, which is the longest distance in the cube, and shorter than the length of the string. Therefore, it doesn't matter were the string is attached, the ant will be able to reach any point within the cube.
Log in to reply
Exactly. The distance between any two points on the cube will be less than the length of the string, so it doesn't matter were the string is attached.
Log in to reply
It says she is on the "outside a solid cube"
But Honey has move along the surface.
Did you just assume his gender
Log in to reply
She's a worker ant, freed from her bonds of servitude. Another hint, though hard to see in the picture, is her little pink collar that spells out "Princess" in rhinestones.
Super easy, you just need to visualise and see that the ant on the leash at the center of the face will reach to the center of the other opposite face, and from then move sideaways from all four directions to cover the entire cube area.
This was easy... the most efficient solution would be to have the leash let honey explore a single, flat face... this would represent the maximum possible coverage. Losses occur when one has to follow a shape that bends toward itself. Imagine a rubber umbrella... folded in on itself, the surface area shrinks. A cube is a plane that is folded in on itself... so the solution must be the one that best avoids these inefficient folds. The vertex is a bad idea as honey immediately encounters faces folding away from the normal of the three adjacent faces. The edge similarly starts where a face is folding toward the adjacent face immediately. Therefore, the best solution must be the one that most closely approximates the “perfect” solution of a single large face... and that would be center of a cube face.
If attached at a vertex honey can not reach the opposite vertex as the distance traveled would be greater than two times the side length ( 2 2 to be precise). So this case is ruled out immediately as with both the edge and face cases honey can reach the opposite point.
When attached to the midpoint of the edge honey can reach the opposite edges midpoint but not the vertices of that corner. In order for that to be possible the leash would have to be ( 5 / 2 + 1 ) l and we know that 5 > 2 since 2 2 = 4 . This is of course greater than two time the side length.
Finally with the leash attached at the centre of a face honey can reach the opposite point and this point so happens to be the longest the leash ever need be to reach any point from this location. To move further, honey goes around the other side, to move left or right of this point the leash shortens.
From the midpoint of an edge the ant indeed can just reach the midpoint of the opposite edge, but not a small distance away. This forbidden distance is in fact 2 - square root 3 (~0.2679) from the edge midpoint in each direction.
But it can easily reach the vertices of that edge, which are only the square root of 3.25 away (~1.803), although by a different route.
Attached at a vertex, the opposite vertex cannot be reached. The forbidden zone is 2 - square root 3 (~0.2679) along three edges from the forbidden vertex, and is square root (8 - 3 x square root 7), (~0.2505) on three faces from the forbidden vertex.
Consider an ant on top of a cone that has an acute point. The area of the cone is defined by the angle of the point. As the angle increases so does the area. The maximum area is when the base of the cone and the upper area are equal. In other words, the angle is 180 degrees, a flat circle. This would lead you to the idea that the area is corner< side< face centre. In other words the face center of a cube will cover vertices with larger angles, therefore more area.
Isn't this the correct answer for all leash lengths (as long as the leash is smaller than 2 times the cube length)?
Yes it is.
My solution came to me when I looked at a rubrics cube and then I realized there is the least amount of diagonals to travel by on the middle of a face. If we think of the hypotenuse of a triangle as the diagonals it becomes clearer that these distances will minimize the ants travel.
The ant can't reach all of the cube in any of the ways of tethering with a length only twice the length of a side. As the diagrams show, if it's tethered on the middle of a face, it needs to be able to reach the midpoint of all four sides on the opposite face, and it can't do that with only twice the length of a side.
Does the leash not free hang? All of the solutions are assumptive the leash follows the surface of the cube. Twice the side length would reach anywhere in the cube from any attachment point.
Below are 2D-overviews of the cube. On the left the leash is attached to the center of a face, in the middle it's on the midpoint of an edge and on the right it's on a vertex.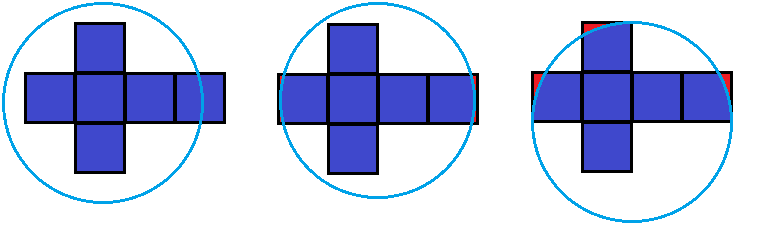
All of the points inside of the circle can get reached.
When the leash is attached on the center of a face, the entire cube can get reached. This might sound strange, because a section of the overview above is outside the circle. These points can still get reached by either traveling to the left, up or down.
When the leash is attached to either the midpoint of an edge or a vertex, there are a few red segment in the overviews that can't get reached. Trying to approach the points from a different angle, as described above, can reduce the amount of unreachable segments more, but it won't become 0.
So the correct answer is on the center of a face