The ant & the wheat

Relevant wiki: Linearity of Expectation

Label the ant's starting vertex with $0$ . Label the three vertices adjacent to the starting vertex with $1$ . Label the three vertices that are adjacent to the vertex with the wheat with $2.$ The vertex with the wheat on it needs no label.

Let $E_{ij}$ be the expected number of edges that the ant has to walk to reach the wheat, given that it is currently at a type $j$ vertex, having reached that vertex from a type $i$ vertex. Then $\begin{aligned} E_{01} & = \; 1 + E_{12} \\ E_{12} & = \; 1 + \tfrac12E_{21} \\ E_{21} & = \; 1 + \tfrac12E_{10} + \tfrac12E_{12} \\ E_{10} & = \; 1 + E_{01} \end{aligned}$ which we can solve to obtain $E_{01} = 5$ , $E_{12} = 4$ , $E_{21} = 6$ , $E_{10} = 6$ . The expected number of edges that the ant has to walk is therefore $1 + E_{01} = \boxed{6}.$

Relevant wiki: Linearity of Expectation

Mark's solution is crazy elegant, but I'll jot mine down anyway.

Using his terminology,

• The first two moves always take the ant to a type 2 vertex.
• Then, flip a coin. If heads, the ant wins in one more move. If tails, the ant wastes some time: it takes either 2 or 4 moves (equally probable, so on average, 3 moves) to return to a type 2 vertex again.

Since the expected number of coin flips it takes to get the first "heads" is well known to be 2, I assumed we would have 2 initial moves + 3 "wasted" moves + 1 "winning" move = 6.

Relevant wiki: Expected Value - Definition

In the discussion under Mark's solution, it was mentioned that we expect an odd value for the number of moves, yet the expectation value is 6. To work this out in more detail, I will determine the probability distribution of the number of steps. This is the long way around to the final answer; Mark shows the fast way!

Let T be the starting point, U one of the three vertices next to it, V one of the three vertices next to the endpoint, and W the endpoint. Let $P(AB, n)$ stand for the probability of reaching the endpoint in $n$ moves, starting at a point op type B after passing through a point of type A. Then $P(VW,0) = 1; \\ P(UV,n) = \frac12 P(VW,n-1) + \frac12 P(VU,n-1); \\ P(VU,n) = \frac12 P(UV,n-1) + \frac12 P(UT,n-1); \\ P(TU,n) = P(UV,n-1); \\ P(\emptyset T,n) = P(UT,n) = P(TU,n-1).$ Here, $n > 0$ , and all expressions for $P(??,?)$ not listed here will be equal to zero.

Define $A_n = P(UV,2n-1)$ . Then clearly $A_0 = 0$ and $A_1 = P(UV,1) = \frac12 P(VW,0) = \tfrac12$ . We write a recursion for $n \geq 2$ : $A_n = P(UV,2n-1) = \frac12 P(VW,2n-2) + \frac12 P(VU,2n-2) \\ = 0 + \frac12 (\frac 12 P(UV,2n-3) + \frac 12 P(UT,2n-3) \\ = \frac14 P(UV,2n-3) + \frac 14 P(TU,2n-4) \\ = \frac14 P(UV,2n-3) + \frac 14 P(UV,2n-5); \\ A_n = \frac14A_{n-1} + \frac14A_{n-2}.$

The standard method for solving this Fibonacci-like recurrence relation is by substituting $A_n = \alpha\ p^n$ ; we have $p^2 - \frac14 p - \tfrac14 = 0\ \ \ \ \ \therefore\ \ \ \ \ p = \frac18(1 \pm \sqrt {17}).$ Thus a general solution of the recurrence relation is of the form $A_n = \frac 1 {8^n}\left(\alpha(1 + \sqrt {17})^n + \beta(1 - \sqrt{17})^n\right);$ but since $A_0 = 0$ we know that $\beta = -\alpha$ , and $A_1 = \tfrac12$ shows that $\alpha = 2\sqrt{17}$ . Thus $A_n = \frac 2 {\sqrt{17}} \frac 1 {8^n} \left((1 + \sqrt{17})^n - (1 - \sqrt{17})^n\right).$ This may be evaluated with a calculator as $A_n = 0.48507\cdot (0.64039^n - (-0.39039)^n),$ or by hand as $A_n = \frac{\sum_{k=0}^{\lfloor n/2 \rfloor} \binom{n}{2k+1}\ 17^k}{2^{3n-2}}.$

Since $A_n$ is the probability of reaching the endpoint in $2n-1$ moves from point V, it is also the probability of reaching the endpoint in $2n+1$ moves from the starting point. To summarize, we find the following distribution:

$\begin{array}{cccr} \hline n & \text{moves} & \text{probability} & \\ \hline 0 & 1 & 0 & 0.000\% \\ 1 & 3 & \dfrac 12 & 50.000\% \\ 2 & 5 & \dfrac 18 & 12.500\% \\ 3 & 7 & \dfrac 5{32} & 15.625\% \\ 4 & 9 & \dfrac 9{128} & 7.031\% \\ 5 & 11 & \dfrac {29}{512} & 5.664\% \\ 6 & 13 & \dfrac {65}{2048} & 3.174\% \\ 7 & 15 & \dfrac {181}{8192} & 2.209\% \\ \hline \end{array}$

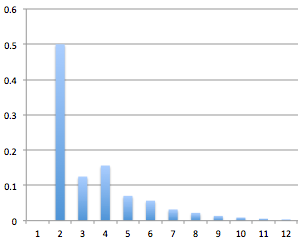
The expected number of moves may be evaluated as $E = \sum_{n = 0}^\infty (2n+1)A_n;$ one of the many ways of doing this is $E = 1 + 2\cdot 0.48507\cdot \left(\frac{0.64039}{(1-0.64039)^2} - \frac{-0.39039}{(1-(-0.39039))^2}\right) = \boxed{6}.$

The expectation value is given by

$\langle n\rangle = \sum_{n}nP(n)$

where $P(n)$ is the probability of getting to the wheat in $n$ moves. Now, we can write this as:

$P(n) = X(n)\frac{1}{3\cdot 2^{n - 1}}$

since all the paths are equally likely. The 3 appears because the first move can be made in three possible ways. $X(n)$ is the number of paths of $n$ steps, say $n$ -paths, which end to the wheat. We calculate this now. Let $O$ be the starting point, $X$ the final point with the wheat, $1,2,3$ the points at one step from $O$ and $A,B,C$ the points at one step from $X$ .

We have the following diagram for the first two steps:

$O \to_{3} (1,2,3) \to_{2} (A,B,C)$

with 6 possibilities. Then, either we end in $X$ in 3 moves, which is the minimum possible number of moves, or we get back to $1,2,3$ . From here, either we get back to $(A,B,C)$ or we pass again through the starting point. We can thus think of two possible loops, one which do not pass through $O$ and which we call $\bar{O}$ -loop and another which does pass through $O$ and which we call $O$ -loop. The $\bar{O}$ -loop is:

$(1,2,3) \to_{1} (A,B,C) \to_{1} (1,2,3)$

It adds two more steps and can be done in only one way, otherwise it ends in $X$ . The $O$ -loop is:

$(1,2,3) \to_{1} O \to_{2} (1,2,3) \to_{2} (A,B,C) \to_{1} (1,2,3)$

It adds 4 more steps and can be done in 4 ways. Missing the wheat in three moves, we can trigger the loops. The two loops add either 2 or 4 steps to the initial 3, therefore the wheat can be reached only in an odd number of steps. Now:

$X(3 + 4n) = 6\sum_{i=0}^{n}\bar{O}^{2n-2i}O^i\frac{(2n-i)!}{(2n-2i)!i!}\\ X(5 + 4n) = 6\sum_{i=0}^{n}\bar{O}^{2n+1-2i}O^i\frac{(2n+1-i)!}{(2n+1-2i)!i!}$

For $3 + 4n$ steps, we need from $2n$ $\bar{O}$ -loops to $n$ $O$ -loops, with all the possible combinations taking into account that each time we remove two $\bar{O}$ -loops we can add an $O$ -loop. The same for $5+4n$ , but here a $\bar{O}$ -loop always remains. The factorials take into account all possible combinations of loops (they are binomial coefficients indeed).

Including the possibilities associated for each kind of loop we have:

$X(3 + 4n) = 6\sum_{i=0}^{n}4^i\frac{(2n-i)!}{(2n-2i)!i!}\\ X(5 + 4n) = 6\sum_{i=0}^{n}4^i\frac{(2n+1-i)!}{(2n+1-2i)!i!}$

These can be summed (I used a software) to give:

$X(3+4n) = \frac{3\ 2^{1-n} \left(4 \left(\sqrt{17}+17\right) \left(9-\sqrt{17}\right)^n+\left(13 \sqrt{17}+85\right) \left(\sqrt{17}+9\right)^n\right)}{17 \left(\sqrt{17}+9\right)}$

and

$X(5+4n) = -\frac{3\ 2^{1-n} \left(32 \sqrt{17} \left(9-\sqrt{17}\right)^n-\left(49 \sqrt{17}+153\right) \left(\sqrt{17}+9\right)^n\right)}{17 \left(\sqrt{17}+9\right)}$

Substituting into the definition of $\langle n\rangle$ we get (again, I used a software)

$\boxed{\langle n\rangle = 6}$

I had 3 guesses. The answer had to be between 3 and 7. 6 was one of my options. Crushed it.

I used a state transition model.

Label 5 states as columns of a spreadsheet: Top (the start location), Down A (have just moved from Top), Down B (have just moved down from A), Up A (have just moved up from B), and Bottom (the wheat). Give Top a starting value of 1, all others 0. In the next row, fill in the transition probabilities: Top to Down A 100%, Down A to Down B 100%, Down B to Up A 50%, etc. Replicate that row several times. Sum (the move number times chance to enter Bottom), and it obviously converges to 6.