The area of a circular ring
The black segment in the diagram is tangent to the inner circle, ends on the outer circle, and is length 5.
Find the area of the circular ring (the blue region).
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
17 solutions
So if I made a circle that was the size of the earth and a circle inside of it that had a radius which allowed the tangent-to-edge-length be 5cm the area would be 25pi???
Log in to reply
Exactly! You can also calculate that, being the Earth Radius R e = 6 3 7 1 k m , your circular ring would be less than 2 m m thick. But its area would still be 2 5 π !
the problem doesn't state that the circles are concentric. do they have to be?
Log in to reply
Yes, a circular ring -or annulus- is defined as the region bounded by two concentric circles :)
The question did not state what is the size of the inner white circle, therefore I can assume that it's radius is 0. Now the question become very simple, the red line become the radius of the purple circle and the answer is 25π
Moderator note:
While this is not a good approach for an "open" problem (where it is uncertain if there's even a unique answer) it's technically correct given that there is a unique answer. This is a good method for solving contest problems (especially in contests where only the answer is desired; for contests that require proof you generally can't assume the answer is unique).
To practice, here's a Martin Gardner puzzle where the same technique works:
A six inch high cylindrical hole is drilled through the center of a sphere. How much volume is left in the sphere?
I know what you are saying, but I feel you can always look at the figure and guess it is not a "point circle". I mean being a person of science and technology does not mean we throw common sense out of the window. That would become a contradictory situation.
Log in to reply
The way the problem is set up, we can assume there is one answer that is true whatever the inner radius is. Since that inner radius could be arbitrarily close to 0, we can assume it is 0, and the answer must be the same. You solve the problem before you, not some other problem. That is common sense.
Log in to reply
Spoken like a true pseudo-scientist!
Log in to reply
@A Former Brilliant Member – I beg to differ. The difference in argumentation is merely in the assumption about whether the given options are to be regarded as a part of the task.
Log in to reply
@Ingo Schalk-Schupp – I beg to differ. The argument is inherently stupid.
This solution seems a little circular to me. You are using the fact that varying the inner radius doesn't change the area to arrive at the answer, but the problem is essentially asking you to prove this fact.
Log in to reply
It isn't - it's merely asking for the area. By giving you options that don't include 'Cannot be determined' or anything to this effect, it is essentially telling you that it doesn't depend on the radius of the inner circle. Of course, this would have to be actually true for the problem to be valid, but making sure the problem is valid is the responsibility of the setter.
This solution is certainly the simplest, and it uses a useful strategy for problem-solving. By looking at extreme cases, the solution to difficult problems can be much more intuitive.
Yes. Since we know it is solvable with just the info given (there is no option "cannot be determined") this is a valid assumption.
Bamboozled
Same here. I knew it is not a complete solution, but I just couldn't resist.
However the black segment is not a radius...even if you say you can assume the white circles radius is 0, that still does not in any way, shape, or form make the drawn segment a radius. That red line does not pass through the center and geometrically speaking would be smaller than the actual radius. The fact that you can get the right answer using inappropriate and illogical means does not make it a valid assumption.
Log in to reply
If you imagine the small circle getting smaller and smaller, the angle of the 5-line with the outer circle approaches 90 degrees. This property would have to be proven if it was a proof, of course.
So funny that I was remembering that Martin Gardner puzzle as I was answering this question, then saw your comment!!! It was from a VERY long time ago, and I remember strenuous objections from a friend as I explained the solution.
Log in to reply
Yes, I have Martin Gardner's book (Mathematical Puzzles and Diversions). In the solution to the 'Hole in the Sphere' problem, both the rigorous solution and the shortcut solution are given, along with this 2D version. You may also wish to look at the post on my profile about this.
bonus question, what can be the maximum/limit radius of the inner circle?
Log in to reply
You can make it close to infinity and area between the circles will still be 2 5 π
that's surprising, good puzzle
Relevant wiki: Circles - Area
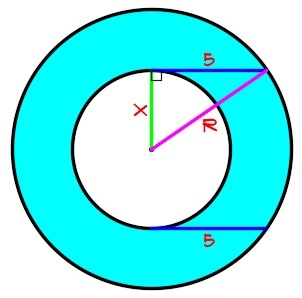 Let
R
be the radius of the big circle and
X
be the radius of the small circle. Consider my diagram. Apply pythagorean theorem in the right triangle. We have
Let
R
be the radius of the big circle and
X
be the radius of the small circle. Consider my diagram. Apply pythagorean theorem in the right triangle. We have
R 2 = X 2 + 5 2 ⟹ R 2 − X 2 = 2 5
The area of the blue region is equal to the area of the big circle minus the area of the small circle, we have
A = π ( R 2 − X 2 ) but R 2 − X 2 = 2 5 , substituting, we get A = π ( 2 5 ) = 2 5 π
The desired answer is 2 5 .
This explanation was more explained in my mind. Thank you
This might be of interest: https://en.wikipedia.org/wiki/Visual_calculus
Nice article. Reminds me of surfaceArea/Volume of revolution!
Of great interest actually. Thanks.
i did i this way
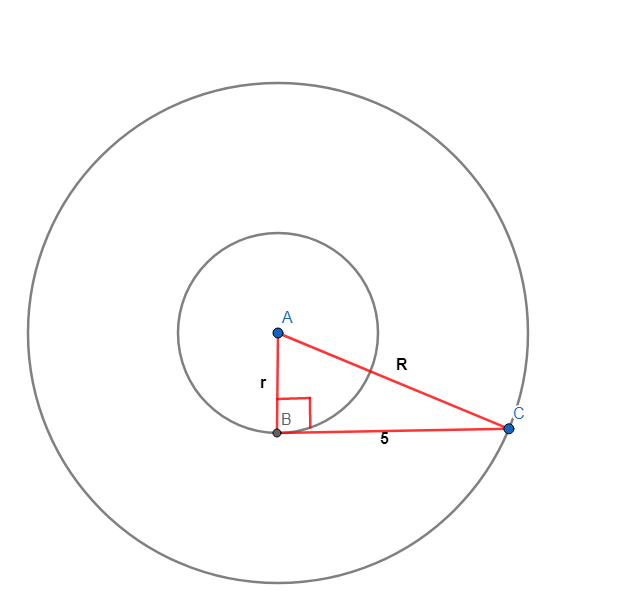
From the diagram above R 2 − r 2 = 2 5 ⟹ the desired area A = ( R 2 − r 2 ) π = 2 5 π .
The area is pi (R^2-r^2) where R and r are the large and small radii repectively. The power of the outer endpoint of the segment with respect to the inner circle is R^2-r^2, but by POP that is also 5^2. Thus the area is 25 pi
EVERYONE HAS THE SAME SOLUTION. I will now show you a much more unique way of solving this problem. We can think about the shaded area as the region swept out by the segment of length 5. So, draw a triangle from the center of the circle to the point where the segment of length 5 is tangent to the inner circle. Now think about rotating that triangle by N degrees. Now, you may notice that as N gets closer and closer to 0, we see a circle traced out, with radius 5. The area of this circle is pi*5^2=25pi.
Use a right triangle with size x and 5. The radius of the great circle is the hypotenuse of that right triangle. The side x is the radius of the inner circle. Now find the solution of the equation: 25pi + pi x^2 - pi x^2 Well that's easy, you get 25 pi
(Can't use latex on my phone, my solution is not the most beautiful)
Everyone has a proper explanation. I just thought you have this side and the other side. 5×5= 25 therefore 25π
Assume that R is the large circle radius and r is the small circle radius.
Through Pythagorean theorem:
R 2 = r 2 + 5 2
The area is the difference between the large and small circle areas:
A = π × R 2 − π × r 2
Replacing R 2 :
A = π × ( r 2 + 2 5 ) − π × r 2
A = π × r 2 + 2 5 π − π × r 2
A = 2 5 π
Aout=PiR2 Ain=Pir2 R2=r2+25 Aou-Ain= pi( R2-r2) = Pi25
Mamikom's proof of pythagorean theorem uses exactly the same approach (i.e. area of annulus, when length of tangent to the inner circle is given.) to show that if the length of the tangent to the inner circle is r then area of annulus = π r 2 . In this case r = 5 , hence A r e a = 2 5 π
Integrate the areas of the isosceles triangles with differential angle between legs of length 5 from 0 to 2 pi. A=1/2 5^2 dTheta. Integrate to get 1/2 5^2 2 pi=25*pi.
Imagine the inner circle radius to be x. Therefore area of the ring is Π(5+x)^2-Πx^2. Taking Π common, it becomes Π(2x+5)*5. Which means that when the given options are divided by 5Π, the quotient left behind is of the form 2x+5, that is the quotient left behind is odd. Of the given options only 25Π satisfies the conditions.
though, not the true way but make the inner circle equals to be a point, the tangent becomes radius and our answer
This is the same solution as Idan Zur.
It is not wrong by itself, but you should have an argument to prove that you're allowed to do so.
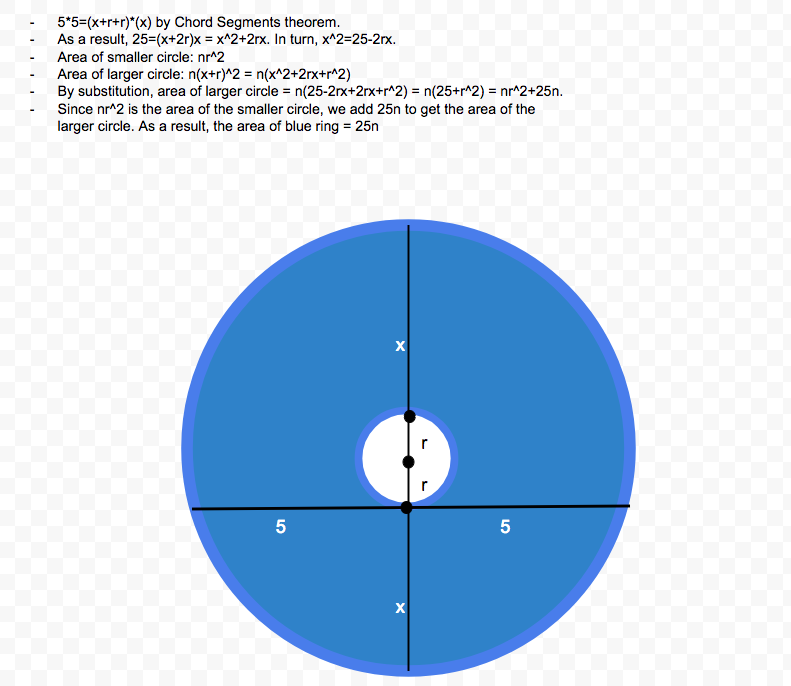
To find the solution, you build a right triangle using the given segment and the radii of the two circles: Now, labeling with
R
and
r
the big and small radius and using Pythagora's Theorem, you have
R
2
−
r
2
=
2
5
, and since the formula for the area of a circular ring is
π
(
R
2
−
r
2
)
, the answer is
2
5
π
.
Now, labeling with
R
and
r
the big and small radius and using Pythagora's Theorem, you have
R
2
−
r
2
=
2
5
, and since the formula for the area of a circular ring is
π
(
R
2
−
r
2
)
, the answer is
2
5
π
.