The Best Friends:- α and β

Algebra Level 3

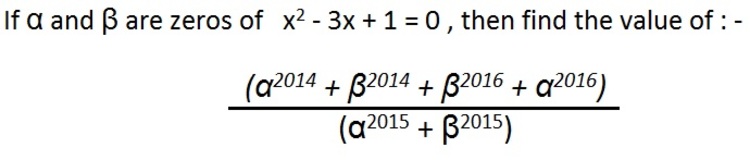This a cool problem. Try it and be cool while solving it......

-1 1 3 100 2016 11 2014 2015

Shivansh Tripathi by Shivansh Tripathi , 22, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Chew-Seong Cheong
Apr 29, 2015

α 2014 + β 2014 + α 2016 + β 2016 α 2015 + β 2015 = α 2014 + β 2014 + ( α + β ) ( α 2015 + β 2015 ) − α β ( α 2014 + β 2014 ) α 2015 + β 2015 = α 2014 + β 2014 + 3 ( α 2015 + β 2015 ) − ( 1 ) ( α 2014 + β 2014 ) α 2015 + β 2015 = 3 ( α 2015 + β 2015 ) α 2015 + β 2015 = 3 \dfrac{\alpha^{2014}+\beta^{2014}+\alpha^{2016}+\beta^{2016}}{\alpha^{2015}+\beta^{2015}} \\ = \dfrac{\alpha^{2014}+\beta^{2014}+(\alpha+\beta)(\alpha^{2015}+\beta^{2015})-\alpha \beta(\alpha^{2014} + \beta^{2014})} {\alpha^{2015}+\beta^{2015}} \\ = \dfrac{\alpha^{2014}+\beta^{2014}+3(\alpha^{2015} + \beta^{2015}) -(1)(\alpha^{2014} + \beta^{2014})} {\alpha^{2015}+\beta^{2015}} \\ = \dfrac{3(\alpha^{2015} + \beta^{2015})} {\alpha^{2015}+\beta^{2015}} = \boxed {3}

6 Helpful 0 Interesting 0 Brilliant 0 Confused

Here's a slightly different way to look at it:

x 2 − 3 x + 1 = 0 ⟺ x ∈ { α , β } ⟹ 3 x 2015 = x 2016 + x 2014 ∀ x ∈ { α , β } x^2-3x+1=0\iff x\in\{\alpha,\beta\}\\ \implies 3x^{2015}=x^{2016}+x^{2014}~\forall~x\in\{\alpha,\beta\}

So, the expression to be evaluated can be rewritten using the result obtained as,

∑ x ∈ { α , β } ( x 2016 + x 2014 ) ∑ x ∈ { α , β } ( x 2015 ) = 3 ⋅ ∑ x ∈ { α , β } x 2015 ∑ x ∈ { α , β } x 2015 = 3 \frac{\displaystyle\sum_{x\in\{\alpha,\beta\}}(x^{2016}+x^{2014})}{\displaystyle\sum_{x\in\{\alpha,\beta\}}(x^{2015})}=3\cdot\frac{\displaystyle\sum_{x\in\{\alpha,\beta\}}x^{2015}}{\displaystyle\sum_{x\in\{\alpha,\beta\}}x^{2015}}=3

Prasun Biswas - 6 years, 1 month ago

Log in to reply

Yes, you are good. i didn't notice that.

Chew-Seong Cheong - 6 years, 1 month ago

Log in to reply

Now, was that sarcasm?

Prasun Biswas - 6 years, 1 month ago

Log in to reply

@Prasun Biswas – No, not sarcasm. I remember I did the same way in another problem. But I have forgotten about it.

Chew-Seong Cheong - 6 years, 1 month ago

Log in to reply

@Chew-Seong Cheong – Ah, okay then. :3

Prasun Biswas - 6 years, 1 month ago

Wow nice solution

Aman Real - 6 years, 1 month ago
Shivansh Tripathi
Apr 27, 2015

1) Take out the values of α and β from the given quadratic equation

2) Then from the product of the roots i.e. (α*β) , take out the value of β in terms of α .

3) Put the value of β (in terms of α) in the part to be solved.

4) In the end you should get α + β , which is = 3.

Wasn't it easy ......................just the question was terrifying . Many are afraid of just looking at this question. Thank You.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

Exercise:

Suppose that α , β \alpha \,,\beta are roots of x 2 − 3 x + 1 = 0 {{x}^{2}}-3x+1=0

What is the value of E ( α , β ) = α 2014 + β 2014 + β 2016 + α 2016 α 2015 + β 2015 E\left( \alpha ,\beta \right)=\frac{{{\alpha }^{2014}}+{{\beta }^{2014}}+{{\beta }^{2016}}+{{\alpha }^{2016}}}{{{\alpha }^{2015}}+{{\beta }^{2015}}}

Solution: we have α & β \alpha \,\And \beta are two roots of p ( x ) = x 2 − 3 x + 1 p\left( x \right)={{x}^{2}}-3x+1 hence p ( α ) = 0 & p ( β ) = 0 p\left( \alpha \right)=0\,\,\And \,p\left( \beta \right)=0

Thus p ( α ) = α 2 − 3 α + 1 = 0 p\left( \alpha \right)={{\alpha }^{2}}-3\alpha +1=0 and p ( β ) = β 2 − 3 β + 1 = 0 p\left( \beta \right)={{\beta }^{2}}-3\beta +1=0

Hence we get ( α 2 , β 2 ) = ( 3 α − 1 , 3 β − 1 ) \left( {{\alpha }^{2}},{{\beta }^{2}} \right)=\left( 3\alpha -1,3\beta -1 \right)

Now back to the E ( α , β ) = α 2014 ( 1 + α 2 ) + β 2014 ( 1 + β 2 ) α 2015 + β 2015 = α 2014 ( 3 α ) + β 2014 ( 3 β ) α 2015 + β 2015 = 3 E\left( \alpha ,\beta \right)=\frac{{{\alpha }^{2014}}\left( 1+{{\alpha }^{2}} \right)+{{\beta }^{2014}}\left( 1+{{\beta }^{2}} \right)}{{{\alpha }^{2015}}+{{\beta }^{2015}}}=\frac{{{\alpha }^{2014}}\left( 3\alpha \right)+{{\beta }^{2014}}\left( 3\beta \right)}{{{\alpha }^{2015}}+{{\beta }^{2015}}}=3

Ramez Hindi - 6 years, 1 month ago

your solution missing important part and many facts

Ramez Hindi - 6 years, 1 month ago

Log in to reply

I do not how to write these lengthy solutions here so I wrote in short .

Shivansh Tripathi - 6 years, 1 month ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...