The Buffon's Needle
 While messing with probability, I came across this problem:
While messing with probability, I came across this problem:
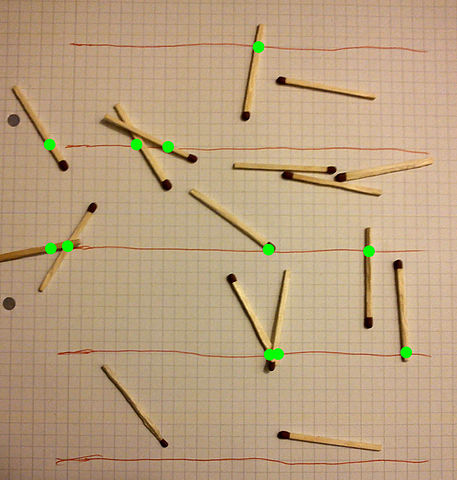
Suppose we have a floor made of parallel strips of wood, each the same width, and we drop a needle onto the floor. What is the probability that the needle will lie across a line between two strips?
Details and Assumptions :
-
Assume that you drop a needle on your rough copy and you have to find the probability that it crosses one horizontal line .
-
Length of needle is equal to separation between two lines.
-
Plane of needle is parallel to plane of floor or you rough copy.
Note: This is famous Buffon's needle problem. If you can,then evaluate the probability 1.) by assuming length of needle is less than separation between two lines and 2.) Length of needle is more than separation between two lines.
Please post a solution assuming all three cases. I'm stuck in the case where length of needle is greater than separation between two lines.
Image Credit: Wikimedia McZusatz
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Awesome problem! I really enjoy doing application of probability problems.
What we will do here is to interpret the problem in probabilistic terms. Assume we have infinite parallel planks on the floor. We can drop our needle wherever we want. Label the midpoint of our needle as M . Dropping the needle consists of the happening of two independent events:
-
The selection of position on floor where point M will land.
-
The selection of orientation(angle) of the needle with respect to the parallel lines on the floor once the needle has landed.
To avoid ambiguity, we will assume our needle to be an arrow, hence, it can make angle 0 through 2 π with the lines on the floor.
Even though 1 and 2 are independent, the happening of 1 will influence the happening of 2. We will see how. Due to the infinite nature of the floor, the probability that M lands on a certain point on the floor is same, regardless of where the point is located on the floor. This means that we can restrict our investigation between two lines as all the other lines behave in the same way. We now continue using the following figure:
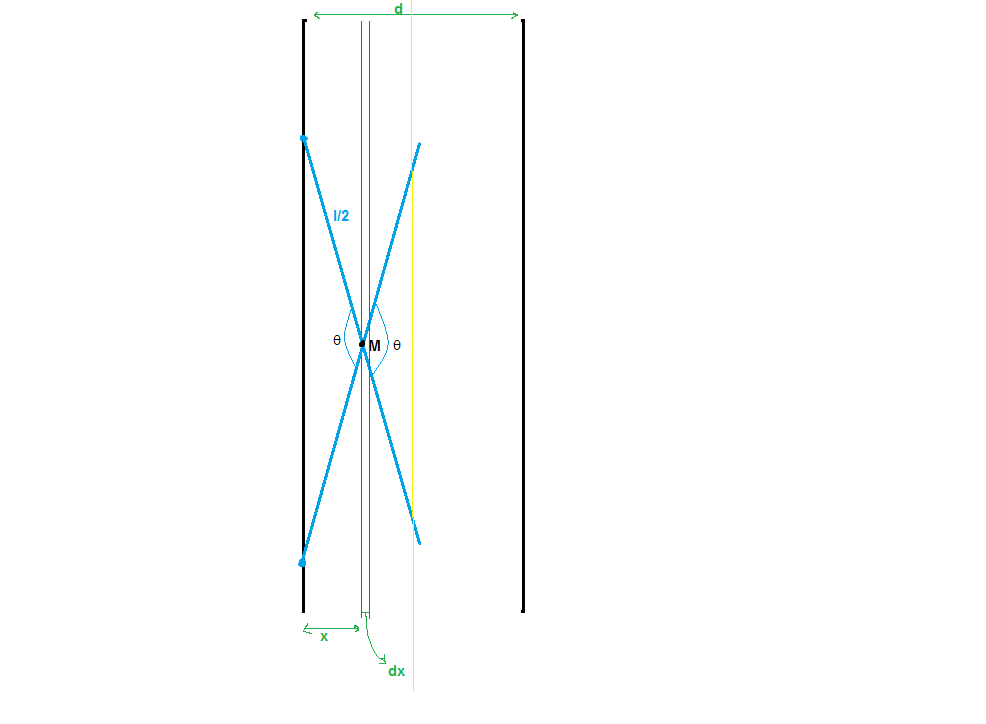
Here, the black lines are the lines on the floor. The distances have been marked. The yellow line is halfway between the black lines. Each blue line represents a fallen needle in a particular configuration. The arrow of needle has been marked. The length of the needle is l . Its midpoint falls in the small region d x which is at x distance from the left line.
Observe that an angle has been marked as θ . We define θ as twice the acute angle that the needle makes with the horizontal when one of it's ends is just touching the left line. Observe that the needle touches the left line for an angular width of 2 θ for each 2 π rotation about point M . This means that after falling, the needle has P 2 = θ / π probability of touching the left line.
We now know the probability of the second event. The probability of the first is simple. It is the probability that M falls on the region d x out of the whole region of length d , i.e: P 1 = d x / d
It is easy to see that: θ = 2 arccos ( l 2 x )
Hence, our required probability for the region d x is:
d P = P 1 × P 2 = d π 2 arccos ( l 2 x ) d x
Observe that there is symmetry in the problem under consideration. The probability is symmetric about the yellow line. Hence, we will simply find the probability for 0 < x < d / 2 and then double it.
Also observe that it may be possible that l 2 x becomes more than 1 for some value of x which is less than d / 2 if l < d . This simply means that the needle may never intersect the left line for some values of x .
Knowing all of the above things we can now integrate our d P function for the left side of the yellow line.
∫ 0 P d P = ∫ 0 k d π 2 arccos ( l 2 x ) d x
Where k is the value of x for which l 2 x = 1 or k = d / 2 , whichever is smaller .
Therefore, since the actual probability P a is double the value of our integral, we have:
P a = 2 ∫ 0 k d π 2 arccos ( l 2 x ) d x
= d π 4 ∫ 0 k arccos ( l 2 x ) d x = d π 2 l [ ( l 2 k ) arccos ( l 2 k ) − 1 − ( l 2 k ) 2 + 1 ]
Hence:
P a = d π 2 l [ ( l 2 k ) arccos ( l 2 k ) − 1 − ( l 2 k ) 2 + 1 ]
For this particular problem, putting l = d and k = d / 2 yields answer as 2 / π .
Log in to reply
What about other two cases ?
Log in to reply
This is the only case. All the three cases have been covered in this. Actually, it is just two cases, when the needle is longer than the width and when it is not, the equal case is included in both of them.
Observe that in the final equation, there is the value of k which has to be substituted in order to get the final formula. The value of k will depend on whether the needle is longer than the width or not, thus accounting for all the cases. Read derivation carefully to understand the importance and the value that k takes in each case.
Log in to reply
@Raghav Vaidyanathan – Oh thanks, I read the solution carelessly, I thought you've mentioned that cases separately. Thanks , once again.
Watch this wonderful video for two different beautiful solutions: MindYourDecisions
Let the two end points of the Needle be A and B . Let the wooden strips be infinite set of horizontal lines with distance between two neighboring lines as R . When the needle drops, the point A of the Needle will fall between a pair of parallel lines. Let the Line immediately below A be the base line h 0 and A 's perpendicular distance from the base line h 0 be x .
No matter where the needle falls, we can always choose the corresponding base line h 0 . Hence, the whole analysis is complete w.r.t. the base line h 0 .
As A can fall anywhere, hence x ∈ [ 0 , R ) .
Point B will lie on a circle of radius R . The needle will lie across a line if point B falls on part of the circumference that falls outside lines h 0 and h 1 .
For a given x , probability that needle lie across a line = P ( x )
P ( x ) = 2 π R 2 α R + 2 θ R = π α + θ = π 1 [ cos − 1 ( R R − x ) + cos − 1 ( R x ) ]
Probability that needle lie across a line P a c r o s s = ∫ 0 R P ( x ) R 1 d x
P a c r o s s = ∫ 0 R π 1 [ cos − 1 ( R R − x ) + cos − 1 ( R x ) ] R 1 d x
Substituting R x = y ,
P a c r o s s = ∫ 0 1 π 1 [ cos − 1 ( 1 − y ) + cos − 1 ( y ) ] d y = π 2 = 0 . 6 3
PS: After solving the problem, I read more about Buffon's needle. Interestingly, one of the application of Buffon's needle simulation is to estimate the value of π .