The Burnt Pancakes

Computer Science Level 1

The cunning chef wants to keep the burnt side of his pancakes down.

To do that, he can only use the flip operation on his stack of pancakes, i.e., he inserts his spatula at some point in between the stack of the pancakes and flips the ones above the spatula, like this:

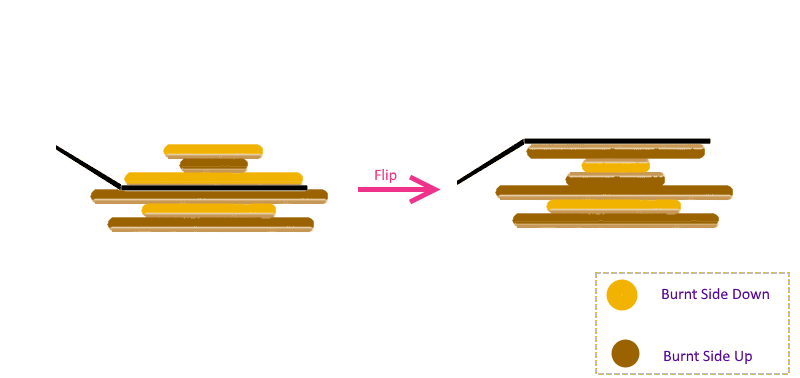
The chef, being cunning, will make sure that he'll fix any stack of pancakes in the least number of flips he can.

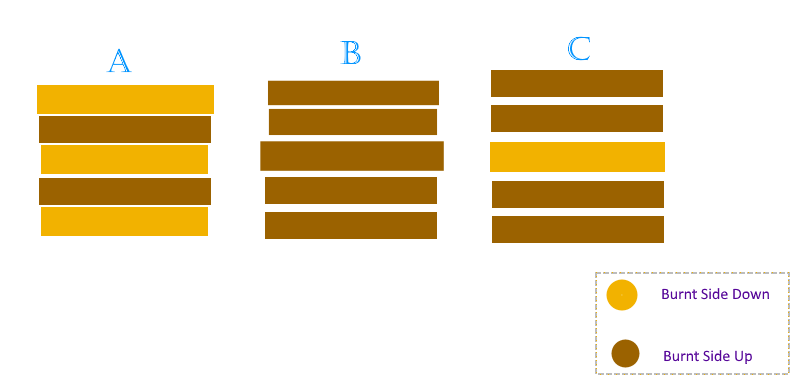
For which one of these three stacks of pancakes would he require the most number of flips?

A B C

1 solution

Geoff Pilling
Feb 11, 2017

Each flip reduces the number of borders (between pancakes of different orientation) by one. (+ 1 extra flip if the bottom pancake is burnt side up.

There are 4 borders in A, no borders in B, (+1 flip), and 2 borders in C (+1 flip).

So, the number of flips for each stack is:

A: 4
B: 1
C: 3

So, $\boxed{A}$ will take the most flips.

This is an interesting way to think about the flips. In particular, this suggests a good way to design an algorithm for the chef to flip his pancakes appropriately.

Agnishom Chattopadhyay - 4 years, 4 months ago

Hmmm, what kind of algorithm are you thinking of? Is it something to do with minimizing the amount of flips needed?

Pi Han Goh - 4 years, 3 months ago

From top to bottom, when first encounter a pancake with opposite burnt side, flip the pancakes on top of it. This action reduces the "border" by one. Repeat this step until the pancakes are all facing the same direction (another flip required if they are facing the wrong direction). Since one flip can resolve at most one border, this algorithm guarantees the minimum amount of flips.

Christopher Boo - 4 years, 3 months ago

@Christopher Boo – Ah nicely done! And I thought we need to think about the famous flipping Pancake problem all over again!

Pi Han Goh - 4 years, 3 months ago

The Burnt Pancakes

1 solution

0 pending reports