The Cardinal Sine Evaluation
 ∫
π
/
6
π
/
2
f
(
x
)
d
x
+
∫
3
/
π
2
/
π
g
(
x
)
d
x
∫
π
/
6
π
/
2
f
(
x
)
d
x
+
∫
3
/
π
2
/
π
g
(
x
)
d
x
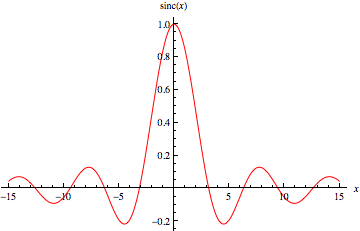
In mathematics the cardinal sine function or sinc ( x ) is defined as f ( x ) = x sin ( x ) . Let g ( x ) denote the inverse function of f ( x ) .
What is the value of the expression given above?
This is an original problem.
Also try The Cardinal Sine Evaluation - Part 2. .
The answer is 0.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The last line should read ∫ π / 6 π / 2 f ( x ) d x + ∫ 3 / π 2 / π g ( x ) d x = sin 2 π − sin 6 π .
Log in to reply
Sorry for the inconvenience.
Log in to reply
Thanks for correcting; you'll want to edit the problem as well.
i mean the problm is with your limits .. 3/pi to 2/pi give 0.5 as answer . but in ur question , limit is from 2/pi to 3/pi .. which will give 0.3036 as ans
The answer is 0.3036 your question is incorrect ! >:(
The relation between f(x) and integral of its inverse g(x) is given by, ∫ a b f ( x ) d x + ∫ c d g ( x ) d x = b d − a c . I n t h i s a = 6 π , b = 2 π , c = π 3 , d = π 2 ∴ I n t . = 2 π ∗ π 2 − 6 π ∗ π 3 = 0 . 5 . This relation is true for any function and its inverse not only for cardinal sine function .
Can you give me proof of the above expression.
\quad In\quad \int _{ \frac { 3 }{ \pi } }^{ \frac { 2 }{ \pi } }{ g\left( x \right) .dx } \quad \\ Let\quad x\quad =\quad f(t)\quad then\quad dx\quad =\quad f^{ ' }\left( t \right) .dt\\ Since\quad g\left( x \right) \quad is\quad inverse\quad of\quad f\left( x \right) ,\\ g\left( f\left( t \right) \right) \quad =\quad t\quad and\quad Using\quad property\quad \\ of\quad change\quad of\quad variable\quad the\quad ,\\ integral\quad becomes\quad :\\ \quad \int _{ \frac { \pi }{ 6 } }^{ \frac { \pi }{ 2 } }{ t.f^{ ' }\left( t \right) .dt } \quad =\quad \int _{ \frac { \pi }{ 6 } }^{ \frac { \pi }{ 2 } }{ x.f^{ ' }\left( x \right) .dx } \\ Now\quad by\quad using\quad integration\quad by\quad parts\quad ,\\ \int _{ \frac { 3 }{ \pi } }^{ \frac { 2 }{ \pi } }{ g\left( x \right) .dx } \quad =\quad \left[ x.f(x) \right] _{ \frac { \pi }{ 6 } }^{ \frac { \pi }{ 2 } }\quad -\quad \int _{ \frac { \pi }{ 6 } }^{ \frac { \pi }{ 2 } }{ f\left( x \right) .dx } \\ \\ \quad \int _{ \frac { \pi }{ 6 } }^{ \frac { \pi }{ 2 } }{ f\left( x \right) .dx\quad +\quad \int _{ \frac { 3 }{ \pi } }^{ \frac { 2 }{ \pi } }{ g\left( x \right) .dx } } =\quad \sin { \frac { \pi }{ 2 } } -\sin { \frac { \pi }{ 6 } } \\ \\ Therefore\quad ,\quad Answer\quad =\quad 0.5\quad