The case of the diminishing circles...

Geometry Level 5

Let $A_{0}$ be a unit circle centered at the origin. Draw another unit circle $A_{1}$ centered at $(0,2)$ , i.e., 'above' and tangent to $A_{0}$ .

Next, moving clockwise, draw a circle $A_{2}$ of radius $\frac{1}{2}$ that is externally tangent to both $A_{0}$ and $A_{1}$ .

Next, continuing to move clockwise, draw a circle $A_{3}$ of radius $\frac{1}{3}$ that is externally tangent to $A_{0}$ and $A_{2}$ .

Continue this process to create a series of circles $A_{n}$ of radius $\frac{1}{n}$ and externally tangent to $A_{0}$ and $A_{n-1}$ , (and to $A_{n+1}$ , once it is drawn).

Let $A_{k}$ be the last circle that can be drawn in this series before $A_{k+1}$ partially overlaps $A_{1}$ . Find $k$ .

The answer is 39.

2 solutions

Brian Charlesworth
Dec 3, 2014

A quick overview .....

Join the centers of $A_{0}, A_{n}$ and $A_{n+1}$ . This will give a triangle with sides length $(1 + \frac{1}{n}), (1 + \frac{1}{n+1})$ and $(\frac{1}{n} + \frac{1}{n+1})$ . Let $\theta_{n}$ be the angle opposite the side joining the centers of $A_{n}$ and $A_{n+1}$ . Then using the Cosine Law and some extensive simplification, we find that

$\theta_{n} = \cos^{-1}(\frac{n(n + 3)}{(n + 1)(n + 2)})$ .

We then need to find $\displaystyle\sum_{n=1}^{k} \theta_{n}$ so that the series of circles has gone far enough around $A_{0}$ so that $A_{k+1}$ overlaps $A_{1}$ on its left side. We can get to $A_{38}$ without any concern, but it does become fussy determining whether $A_{39}$ or $A_{40}$ is the first to overlap $A_{1}$ from the left. It turns out that $A_{39}$ is clear by a whisker, giving us $\boxed{k = 39}$ , but I will leave the details until the morning.

I wonder if one could generalise this problem to $S = \sum_{i=1}^{\infty} r_{i}$ a divergent sum.

Jake Lai - 6 years, 6 months ago

Hmmm.... I'm not sure. Since we're dealing with the harmonic series we know that the series of circles, if allowed to continue, will keep circumnavigating the circle without end, but I don't think we can 'prove' that the harmonic series is divergent base on this problem.

We know that $\lim_{n \longrightarrow \infty} \theta_{n} = 0$ , but that doesn't tell us anything regarding convergence/divergence.

Brian Charlesworth - 6 years, 6 months ago

I have an issue with your formula, Brian. When n = 1 is substituted in the formula we get an angle of 48... degrees, but that is the angle from the vertical to the center of circle n = 2.

However, I do agree with your contention that the last circle is #39. Check my results obtained by means of an Excel spreadsheet: Corroboration

Guiseppi Butel - 6 years, 6 months ago

@Guiseppi Butel – Yes, $\theta_{n}$ as defined is the angle between (i) the line segment joining the origin to the center of $A_{n}$ and (ii) the line segment joining the origin to the center of $A_{n+1}$ . I guess a different indexing would have been more intuitive, but I think that the formula as defined is correct.

So to calculate the clockwise angle from the vertical to the line segment joining the origin to the center of $A_{39}$ would mean the calculation of $\displaystyle\sum_{n=1}^{38} \theta_{n}$ .

Perhaps I should have started with the top circle being $A_{0}$ , then the indices would have been more, well, indicative, but at this point I'm just going to leave my indexing as it is. :)

P.S.. Thanks for confirming the answer of $39$ . That last circle makes it in by a whisker .

The full series of circles does make for a display of mathematical art .

(EDIT: I should have credited these diagrams to an acquaintance, Al P. Sorry for the initial oversight.)

P.P.S.. I hope that you got my note regarding your problem, "The Shrinking Square". It's a great problem, (I had to think about for a day before figuring out how best to approach it), but I want to make sure our answers coincide before re-sharing it.

Brian Charlesworth - 6 years, 6 months ago

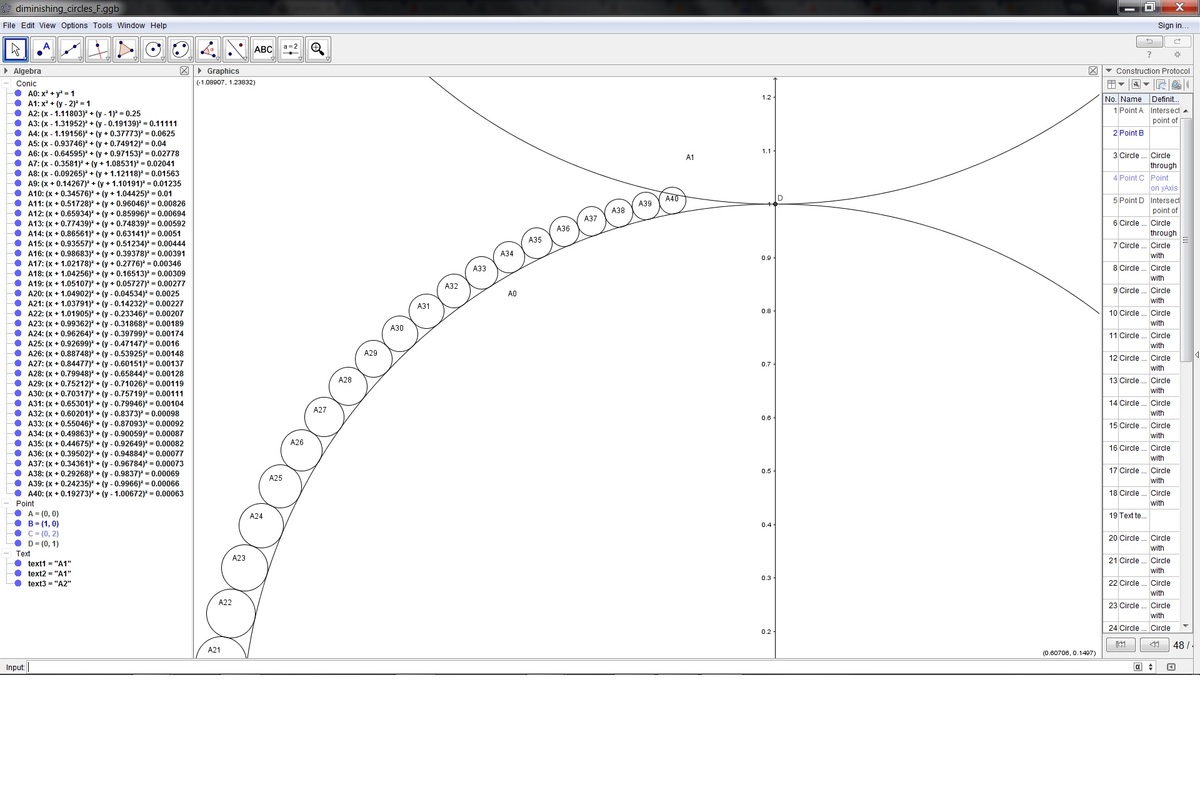
@Brian Charlesworth – Here's your mathematical art on geoegebra:

there are 38 circles here but Im sure the answer is 39 since for that pic above, I just estimated the coordinates of the circle's centers

Julian Poon - 6 years, 6 months ago

@Julian Poon – Cool. Thanks for doing this, Julian. It sort of looks like some exotic creature with its tail wrapped around its abdomen. :)

Brian Charlesworth - 6 years, 6 months ago

@Brian Charlesworth – I'm having second thoughts about the correctness of my answer in "The Shrinking Square" problem. I now feel that one of my assumptions was not correct. If your answer doesn't match with mine I wouldn't be surprised. I did not take into consideration the decrease in the arc length of the intersection in one point in the shrinking process.

Guiseppi Butel - 6 years, 6 months ago

@Guiseppi Butel – Yes, the lack of symmetry makes this a particularly difficult problem. That was why I rotated the circle and square around $O$ so that the sides of the square were horizontal and vertical. This allowed for a much easier integral calculation, from which I found a side length value of $5.8797$ to $4$ decimal places. I'll be interested to hear of the results of any re-examination you might make of your method.

Brian Charlesworth - 6 years, 6 months ago

@Brian Charlesworth – What do you get for the area of the intersection at the beginning of the process?

Guiseppi Butel - 6 years, 6 months ago

@Guiseppi Butel – @Guiseppi Butel I just noticed that "The Shrinking Square" got reshared by Peter Taylor, which means that it will get quite a wide audience. It would probably be a good idea to change the answer soon before someone else reports the question. (This is why I only re-share after I'm certain that the posted answer is correct; otherwise, people may end up getting frustrated in trying to get the question right.)

Brian Charlesworth - 6 years, 6 months ago

@Brian Charlesworth – After my last query I went back over my figures and discovered that I made the fundamental error of not applying the test of reasonableness to my answer before submitting it to public scrutiny. I now find that the answer is less than 6 and much greater than the 4... which I submitted. I would say that your answer meets the test of reasonableness, and suggest that you submit it in your report. My skill at calculus is at an introductory level and not quite up to integrating on functions which involve 2 variables.

I had devised another problem in this series which involved a rotating square and a circle which I now realize involved mathematics quite beyond my level of expertise. I would gladly give you the details for your examination. I can't submit it to this forum because I can't find a solution.

Guiseppi Butel - 6 years, 6 months ago

@Guiseppi Butel – For "The Shrinking Square", I first rotated the circle and square by $\arctan(2)$ to get the sides parallel to the $x,y$ axes. The new coordinates for $A$ were then about $(0.1305, 3.789)$ . I then found where the extended sides intersected the circle, and then found the area contained within the circle. Here is that calculation.

I then took this value, $17.2855$ , as half the area of the desired square, multiplied by $2$ and then took the square root to get the side length of the square, resulting in the $5.8797$ value.

I can't submit an answer to the question as it is because I haven't submitted the value you have posted as the solution, so I'm not sure how to proceed. One possibility is that you could have the answer changed to $5.8797$ , after which I could post my solution method, re-share the problem and see if my answer stands up to scrutiny from our peers. Whatever you choose to do is fine with me; the question is a good one and deserves an audience.

Your rotating square/circle question sounds intriguing; I was guessing that might be the next type of question in your series. You could post it as a note and then I and the community could give it a try, or you could share the specifics with me to get some initial feedback.

Brian Charlesworth - 6 years, 6 months ago

@Brian Charlesworth – I'm puzzled, Brian. Did you account for the missing part of the intersection area, where the one axis didn't quite meet the curve? (at B) Final graph

Guiseppi Butel - 6 years, 6 months ago

@Guiseppi Butel – It turns out that the diagram as you have shown does not have half the square's area inside the circle and half out. My solution square has both $B$ and $D$ outside the circle, (which I wasn't expecting). The graph of my (rotated) solution square is here .

The circle extends far enough beyond the diagonal of the square that the area beyond the diagonal compensates for the area "lost" due to the fact that $B$ and $D$ lie outside the circle. I was expecting something more like your diagram, but I've double-checked my calculations. I also looked at what happened if $B$ lay on the circle, and this left me with a square that had more than half its area inside the circle, so I knew that $B$ for the solution square did have to lie outside the circle.

Brian Charlesworth - 6 years, 6 months ago

@Brian Charlesworth – I, also was expecting B is to be inside the circle. That's what was troubling me. In that case it's just a matter of finding the side of the square that is double the area of the initial intersection. I found that area to be 18.23488 compared to your area of 17.2855. I did mine by subtracting the area of the 2 triangles from the area of the sector. I may have erred in my computations, however.

Why did you not integrate from x= 0 to the upper limit?

Guiseppi Butel - 6 years, 6 months ago

@Guiseppi Butel – When I rotated the square by $\arctan(2)$ I had point $A$ end up at $(0.1305, 3.789)$ , so I had to set the lower limit of the integral at $0.1305$ instead of $0$ .

I have just tried your approach of subtracting the areas of the two triangles from the area of the sector and got a value of $17.2838$ , which translates to a square side value of $5.8794$ , which is within a whisker of the $5.8797$ value I obtained using integration, (the difference probably just due to rounding). So to $2$ decimal places I would say that $5.88$ is looking like a viable answer to go with. I will check both methods again later to be absolutely certain, but for now, I'm pretty confident with this value.

Brian Charlesworth - 6 years, 6 months ago

@Brian Charlesworth – I found my error. It was in the area of one of my triangles. I inadvertently referred to the wrong angle. I now get 5.8797. I guess I'll go with 5.88 in my report. You can supply the solution because you were the one that solved it. Thanks for the patience and your interest.

My e-mail address is [email protected] if you are interested in "The Twirling Square" problem. If you can solve it, I will post the problem with your answer. I don't have the expertise required to crack this one. Hoping to hear from you.

Guiseppi Butel - 6 years, 6 months ago

@Brian Charlesworth – The area I calculated was 17.28554528 giving 5.87971858 for the side of the square. Very fine whisker!

Guiseppi Butel - 6 years, 6 months ago

@Guiseppi Butel – Great. I'm glad the two methods are in agreement. Hopefully the moderator will update the answer soon so that the question can be un-flagged and I can post a solution.

Thanks for the e-mail. I'll give "The Twirling Square" a whirl later today; looks like a fun problem. :)

Brian Charlesworth - 6 years, 6 months ago

Hey hi fellow Singaporean! Anyway, I did this and this . In other words I bashed it out, manually...

Wolfram Alpha tells that it doesn't have a finite limit here

Julian Poon - 6 years, 6 months ago

Bob Kadylo
Jan 9, 2016

I used GeoGebra just like Julian Poon did. The circle centres were calculated with the help of WolframAlpha. I zoomed in to the critical area to see that A40 is the first circle to touch A1.

Moderator note:

Thanks for sharing the diagram!

The case of the diminishing circles...

The answer is 39.

2 solutions

Moderator note:

0 pending reports