The Circumcircle And The Tangents

I shall use the following fact numerous times without mention in my solution.

Fact: If $S$ is the circumcenter of a triangle $\triangle PQR$ , $\angle SPQ = 90^{\circ} - \angle QRP$ .

The proof of this very simple fact is left to the reader.

We shall work with the following configuration. The solutions for other configurations follow analogously.

Image link: http://s27.postimg.org/6k3m431s3/Untitled.png

Let $O_1$ and $O_2$ be the centers of $\omega_1$ and $\omega_2$ respectively. Note that $O_2A \perp AY,$ and $\angle BAO_2 = \angle YAO_2 - \angle YAB = 90° - \angle YAB.$ But since $O_2$ is the circumcenter of $\triangle BAX,$ $\angle BAO_2 = 90^{\circ} - \angle BXA,$ and consequently $\angle BXA = \angle YAB.$ Now, $\angle BXA + \angle BAX = \angle YAB + \angle BAX = \angle YAX,$ so $\angle ABX = 180^{\circ } - \angle YAX.$ Similarly, $\angle ABY = 180^{\circ} - \angle YAX,$ and $\angle YBX = 360^{\circ} - \angle ABY - \angle ABX = 2 \angle YAX = \angle YOX,$ so quadrilateral $YBOX$ is cyclic.

Finally, $\begin{array}{lcl} \angle ABO & = & 360^{\circ} - \angle YBA - \angle YBO \\ & = & 360^{\circ} - \angle YBA - (180^{\circ} - \angle OXY) \\ & = & 180^{\circ} + \angle OXY - \angle YBA \\ & = & 180^{\circ} + 90^{\circ} - \angle XAY - (180^{\circ} - \angle XAY ) \\ & = & \boxed{90^{\circ}}. \end{array}$

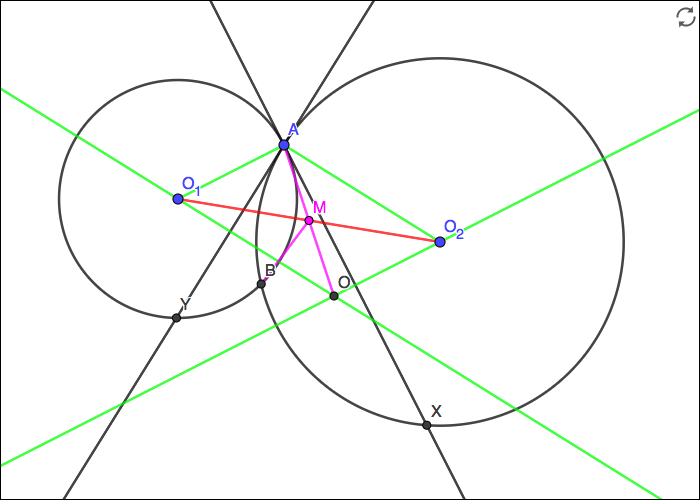
Let the centers of $\omega_1$ and $\omega_2$ be $O_1$ and $O_2$ respectively.

Notice that both $O$ and $O_1$ are on the perpendicular bisector of $AY$ . Thus, $OO_1 \perp AY$ . However, $AO_2 \perp AY$ as well since $AY$ is tangent to $\omega_2$ , so $OO_1 \parallel AO_2$ . Analogously, $OO_2 \parallel AO_1$ , so $AO_1OO_2$ is a parallelogram.

Thus, letting $M$ be the intersection of $O_1O_2$ and $AO$ , we have $AM = MO$ . However, since $O_1O_2$ is the perpendicular bisector of $AB$ , we also have $AM = MB$ . Thus, the center of circle $(ABO)$ is $M$ , and since $AO$ is a diameter, $\angle ABO = 90$ .

Draw the circumcircle produce AB so that it cuts the circumcircle at Z. Now join the point O with Z and A. Now OA is equal to OZ(radius of circumcircle). <OZB= <OAB (as OZA is a isosceles triangle) & OB is common to triangle OZB and OAB, therefore triangle OZB is congruent to triangle OAB. So BZ is equal to AB, therefore OB is perpendicular to AB as OB is line from center and dividing the chord of the same circle equally.

Diagram of the problem suggests the answer is 90. Draw N the midpoint of AY and M of AX. Then we need to prove ANMBO is concyclic because then $\angle ABO= \angle AMO=90$ since radical axis is perpendicular to line between centers: (if $O_1$ the center of $W_1$ and $O_2$ of $W_2$ then $O_1O_2$ is perpendicular to AB, O 1O is perpendicular to AY, O 2O is perpendicular to AX). Now note that $\angle AYB=\angle XAB$ (tangency) and $\angle BXA=\angle BAY$ (tangency). So triangle $YBA$ is similar to triangle $ABX$ . Then clearly traingles $NBA$ and $MBX$ are similar, so $\angle BMA=180-\angle BMX=180-\angle BNA=\angle BNY$ . So then $ANBM$ is cyclic. Also $ANMO$ is cyclic since $AMO=ANO=90$ . $\square$