The dance of the planets
Consider three planets of masses m 1 = m ∗ , m 2 = m ∗ / 2 and m 3 = m ∗ / 3 located at the vertices of an equilateral triangle with sides of length d . It turns out that the planets, under the action of the mutual forces of gravitation, can move in such a way that they always form an equilateral triangle of variable side d ( t ) . Assume that maximum and minimum distances between the planets are d m a x = 2 × 1 0 6 km and d m i n = 5 × 1 0 5 km and that after T = 3 × 1 0 5 s the planets return to their original configuration shown in the figure. That is, T is the period of the orbital motion of the planets. Using the information provided, determine the maximum speed in kilometers per second of planet m 1 .
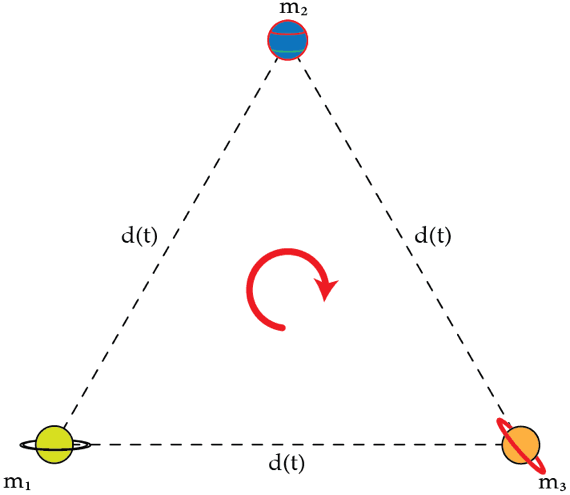
Details and assumptions
The universal gravitational constant is G = 6 . 6 7 × 1 0 − 1 1 m 3 kg − 1 s − 2
The answer is 20.74.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Fantastic! +1.
Great solution, sir!
Never knew the formula for velocity of planet, thank you very much for sharing the solution. :)
Log in to reply
I think if you go through your calculation and leave everything in symbols until the last step, you'll see that you derived the formula yourself!
This was really a fun problem. I had my answer marked wrong initially. I later received an e-mail from Brilliant stating that my answer is correct. I was overfilled with joy knowing that I was able to solve the problem. Many thanks to the Brilliant staff. :)
Here's what I did:
Notice that the net force on each particle passes through the centre of mass of the planet system.
Since the CoM is at rest, each planet orbits around the CoM as Earth orbits around the Sun. So we can safely say that each planet has an effective Sun placed at the CoM of the system.
The problem asks the maximum speed of m 1 so lets find out the net force acting on it.
There are two forces acting on m 1 , one ( F 1 ) along the line joining m 1 and m 2 and the other ( F 2 ) along the line joining m 1 and m 3 .
Define F = d 2 G m 2 .
Clearly, F 1 = F / 2 and F 2 = F / 3 . The resultant of these two forces is
F n e t = 6 1 9 F = 6 1 9 d 2 G m 2
Since, m 1 orbits around the CoM, we need its distance from the CoM. Lets call it r ( t ) .
I skip the proof as it can be easily calculated. It comes out to be:
r ( t ) = 2 2 2 1 9 d = 7 2 1 9 π d
d ( t ) = 2 1 9 7 π r ( t )
Subbing this in the F n e t , we get:
F n e t = 1 4 7 π 2 3 8 1 9 r 2 G m 2
The above implies that m 1 orbits around the effective Sun of mass 1 4 7 π 2 3 8 1 9 m . Call it M e f f .
So the situation is something like this:

The semi-major axis of the ellipse shown is 2 r m a x + r m i n .
But
r = 7 2 1 9 π d
Hence, a = 7 π 1 9 ( 2 d m a x + d m i n )
Subbing the values for d m a x and d m i n ,
a = 7 π 1 9 × 2 5 × 1 0 8 metres
The question gives us the time period of orbital motion. Time to use Kepler's Third Law! i.e
T = 2 π G M s a 3
In our case, M s = M e f f . Plugging in the values, we get m = 7 × 1 0 2 7 . Click here for the calculations .
Next steps involve conservation of angular momentum about M e f f and conservation of energy. We use these at the points at distances r m a x and r m i n from M e f f .
From conservation of angular momentum, r m a x v m i n = r m i n v m a x ⇒ v m i n = v / 4 , where v = v m a x . Its quite easy to see why the velocity is minimum at maximum distance or velocity is maximum when the planet is at the minimum distance.
Using conservation of energy,
r m a x − G M e f f m + 2 1 m 1 6 v 2 = r m i n − G M e f f m + 2 1 m v 2
Lets simplify the potential energy term. The potential energy is:
r − G M e f f m = 7 π 2 1 9 d − G m 2 1 4 7 π 2 3 8 1 9 = 2 1 π d − 1 9 G m 2
So our energy equation changes to:
2 1 π 1 9 G m ( d m i n 1 − d m a x 1 ) = v 2 ( 2 1 − 3 2 1 )
Solving for v ,
v = 2 0 . 7 4 3 m/s
Click here for the calculations
Hence, maximum velocity of m 1 is 2 0 . 7 4 3 km/s .
Typo: At the end of solution, its 20743 m/s instead 20.743 m/s.
First let us find center of mass at P (say). Let m 1 , m 2 , and m 3 be at A , B , and C respectively,Let Y axis be along altitude from A and X axis perpendicular to it.In whole of solution , m ∗ has been changed to m .
Clearly, X c m = 6 1 1 m 2 m 2 d − 3 m 2 d = 2 2 d
Y c m = 6 1 1 m 6 5 m 2 d 3
Now , we note that F n e t y = 2 d 2 G m 2 2 3 + 3 d 2 G m 2 2 3 = 1 2 d 2 5 3 G m 2 , and
F n e t x = 2 d 2 G m 2 2 1 − 3 d 2 G m 2 2 1 = 1 2 d 2 G m 2
Hence F n e t x F n e t y = Y c m X c m ,implying that the angle made by net force with altitude is same that made by line joining A and P , thus the net force on it is always directed towards cm, which is stationary, and hence it behaves as the focus of elliptical orbit of planets.
A P = h = X c m 2 + Y c m 2 = 1 1 1 9 d = γ d (say),
Let us say an effective mass M is attracting the planet A ,
In the elliptical orbit, semi-major axis = 2 h m a x + h m i n = 2 γ ( d m a x + d m i n ) = a (say)
Now, T 2 = G M 4 π 2 a 3 ⇒ G M = T 2 4 π 2 a 3
Energy of planetary motion = h − G M m + 2 1 v 2 = 2 a − G M m
Clearly, velocity will be max when h is min., hence,
2 1 m v m a x 2 = G M m ( h m i n 1 − h m a x + h m i n 1 )
⇒ v m a x 2 = 2 a 2 G M h m i n h m a x
= 2 a T 2 8 π 2 a 3 d m i n d m a x
⇒ v m a x = T 2 π a d m i n d m a x
= T π γ ( d m a x + d m i n ) d m i n d m a x = 2 0 . 7 4 3 K m / s :)
We label the planets P 1 , P 2 , P 3 , where the planet P i has mass m i . For typing convenience, we define m = m 1 .
Consider an instant when the length of the equilateral triangle is L . First, we assign coordinates to the planets. Let P 1 be placed at the origin, and let the straight line joining P 1 and P 3 be the x − axis. Using simple trigonometry, we can calculate the coordinates of the other planets:
 If the image doesn't load, go to:http://s23.postimg.org/6rfl4i1gr/Untitled.png
If the image doesn't load, go to:http://s23.postimg.org/6rfl4i1gr/Untitled.png
Now, we compute the coordinates of the center of mass: ( x c m , y c m ) = ⎝ ⎜ ⎜ ⎛ m + 2 m + 3 m L × 3 m + 2 L × 2 m , m + 2 m + 3 m 2 3 L ⎠ ⎟ ⎟ ⎞ = ( 2 2 7 L , 2 2 3 3 L ) Now we try to compute the net force acting on P 1 . For sanity sake, let k = L 2 G m 2 . This substitution will simplify our calculations later.
The magnitude of the force on
P
1
due to
P
3
is given by
∣
F
3
1
∣
=
L
2
G
m
3
m
=
3
k
The magnitude of the force on
P
1
due to
P
2
is given by
∣
F
2
1
∣
=
L
2
G
m
2
m
=
2
k
Notice that the angle between these vectors is
6
0
∘
. The magnitude of their resultant will be given by
∣
F
3
1
+
F
2
1
∣
=
(
3
k
)
2
+
(
2
k
)
2
+
2
.
3
k
.
2
k
.
cos
(
6
0
∘
)
=
6
1
9
k
Now let
θ
be the angle
F
3
1
+
F
2
1
makes with
F
3
1
. We can compute
θ
from the well known rules of vector algebra as follows:
tan
(
θ
)
=
∣
F
3
1
∣
+
∣
F
2
1
∣
cos
(
6
0
∘
)
∣
F
2
1
∣
sin
(
6
0
∘
)
=
3
k
+
2
k
.
2
1
2
k
.
2
3
=
3
3
7
 If the image doesn't load, go to: http://s23.postimg.org/wu9mycr1n/Untitled.png
If the image doesn't load, go to: http://s23.postimg.org/wu9mycr1n/Untitled.png
Notice that tan ( θ ) is also equal to the slope of the line joining P 1 and the COM. In other words, the resultant force vector passes through the COM.
Now, let's try to find the distance from P 1 to the COM. This is simply x C M 2 + y C M 2 = ( 2 2 7 L ) 2 + ( 2 2 3 3 L ) 2 = 1 1 1 9 L
We shall now place an imaginary star at the center of mass such that the force it exerts on P 1 is equal to the net force acting on P 1 . Let the mass of this star be M s . The magnitude of the force it exerts on P 1 is given by ∣ F s 1 ∣ = ( 1 1 1 9 L ) 2 G m M s = 1 9 1 2 1 k M s This is equal to ∣ F 3 1 ∣ + ∣ F 2 1 ∣ = 6 1 9 k . Equating them, 1 9 1 2 1 k M s = 6 1 9 k ⟹ M s = 7 2 6 1 9 1 9 m Now, notice that if we replace the planets P 2 and P 3 by a star with mass 7 2 6 1 9 1 9 m at the COM, the motion of P 1 doesn't get affected. This follows immediately from our previous observations.
Also note that since no external force acts on the system P 1 P 2 P 3 , the position of the COM remains fixed. In conclusion, the equilateral triangle △ P 1 P 2 P 3 with length L corresponds to the planet P 1 revolving around a star which is fixed at the COM, the orbital distance being 1 1 1 9 L .
We know that the maximum value of L is L m a x . This corresponds to the planet being at the farthest point from the star, the orbital distance at that moment being r m a x = 1 1 1 9 L m a x . Again, the minimum value of L being L m i n corresponds to the planet being at the farthest point from the star, the orbital distance being r m a x = 1 1 1 9 L m i n .
 If the image doesn't load, go to: http://s28.postimg.org/y1us1iv25/Untitled.png
If the image doesn't load, go to: http://s28.postimg.org/y1us1iv25/Untitled.png
From Kepler's First law, we know that the trajectory of P 1 is an ellipse with the star at one of its focii. The length of the semi-major axis is given by a = 2 r m i n + r m a x = 2 2 1 9 ( d m i n + d m a x ) From Kepler's Third law, we know that the time period of the orbit is given by T = 2 π G M s a 3 ⟹ G M s = 4 π 2 a 3 T The maximum velocity of P 1 is attained when it is closest to the star(see here ). The velocity is given by v m a x = r m a x a r m i n G M s We plug in everything to get v m a x ≈ 2 0 . 7 4 kilometers per second
Hi, nice explanation and images, are they made at ms paint, please tell!
Log in to reply
Yes! To be precise, I used the version of mspaint for windows 7, which is very powerful if you know how to use it. :)
Log in to reply
Hi, how you insert r min and r max , are you copying it as an image from somewhere and then pasting.
Log in to reply
@Jatin Yadav – Yes. The process is simple:
- Open a random discussion in Brilliant, and type your LaTeX code there.
- Press the "Preview" button, zoom your browser window, and capture a screenshot.
- Open up another window in mspaint, and paste your screenshot there.
- Crop the LaTeX code, and paste it in your original image.
That's all! ;)
Log in to reply
@Sreejato Bhattacharya – You can do it more simply... Just download the screenshot tool Lighshot and you will be able to copy any portion in your screen by just pressing the print screen key in your keyboard and then selecting the desired portion... A lot easier... You don't have to copy the screenshot and then crop, instead you can directly crop from the original scree... Try it, you'll surely love it... :)
Nicely done Sreejato. ;)
I see that you misplaced the CoM, don't you think it should be nearer to the heaviest planet? :)
Log in to reply
Yes, sorry for that. And I believe I also reversed the direction of F 3 1 . :)
very nice solution thanks
First, let us convince ourselves that each of the planets moves in an elliptical orbit. As the planets maintain an equilateral triangle formation, and there is no external torque on the system, there must be a symmetry about the center of mass. The planets can move about it but they must maintain the same relative distance and orientation to the center of mass at all times.
Each planet is attracted by the pull of each of the two other planets towards a point somewhere in between them, the exact coordinates of which are determined by their relative masses and the orientation of the equilateral triangle. This is given by the center of mass.
Each planet experiences an attraction in a constant direction relative to the equilateral triangle formed by the planets. This amounts to an effective central force and therefore gives rise to an elliptical orbit. From here on, we'll assume the tools of central force motion and use the geometry and period provided to calculate an effective μ , the gravitational parameter that appears in usual two body problems.
Due to the symmetry of the problem, the planets are in aphelion (furthest point in their orbit from their focus) and perihelion (closest point) at the same time. Therefore, when the planets are furthest from one another, they are furthest from their focus, and when they're closest to one another they are closest to their focus. As the focus is the center of mass, we can easily calculate the distance from m 1 to the center of mass at aphelion.
With m 1 as the origin, the x -coordinate of the center of mass is given by
x C.O.M. = M ∗ ( 1 + 2 1 + 3 1 ) 2 1 d m a x 2 1 M ∗ + d m a x 3 1 M ∗ = 2 2 7 d m a x
Similarly, the y -coordinate is given by
y C.O.M. = M ∗ ( 1 + 2 1 + 3 1 ) 2 3 d m a x 2 1 M ∗ = 3 2 2 3 d m a x
The distance from m 1 to its focus, the center of mass, is given by
d C.O.M. = x C.O.M. 2 + y C.O.M. 2 = 1 1 1 9 d m a x
At perihelion, the geometry is the same but with all lengths scaled down by a factor of d m i n / d m a x
With all this, we can easily calculate the length of the semi-major axis a
For any elliptical orbit, we know that the period is related to the semi-major axis by
T = 2 π μ a 3
where μ is the standard gravitational parameter describing the mass of the system. Since ours is a three body problem mapped onto a two body problem, we'll have some effective parameter μ e f f to describe the system. Since we know T and a , we can say
μ e f f = 4 a 3 π 2 / T 2
For any elliptical orbit, the velocity of a planet at any distance r from its focus which, at aphelion, is given by
μ ( r 2 − a 1 ) = 1 − e 1 + e a μ
The velocity of a planet at perihelion is the greatest at any part of its orbit since its radius is smallest (conservation of angular momentum).
Our eccentricity e is given by the difference between the aphelion and perihelion distances over their sum which in our case reduces so
e = d m i n + d m a x d m i n − d m a x
Putting this all together and using the distances and period provided in the problem, we find
v m a x = 1 − e 1 + e a μ = 3 3 5 0 1 9 π s km .