The definite integral that was indefinitely long
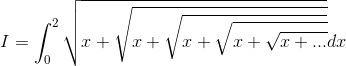
If I = p / q for coprime positive integer p , q , what is p − q .
The answer is 13.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
@Md Zuhair is my solution correct because i don't have official answers.
Log in to reply
Ya it seems. As I have got the same results. And also you must mention that for positive sq root we will neglect the neglect the negetive root. Otherwise it seems fine
No there is a mistake. You need to change the upper limit and lowerlimit as per your substitution
How cube root became 27???? I see many mistakes
Yes that is all right i treated it as indefinite integral for the time being then introduced limits and back substituted.Oh sorry it is not 4x+1 ^ (2/3) it is 4x+1^(3/2) so sorry i used latex for first time so did some mistakes.next time will use pen paper and upload image.latex is so much easier on brilliant just a click of a button.
Log in to reply
No I think latex is easier. See CS is a nice subject if you know the concepts and some thing u hav to keep in memory.
You need to show how you concluded that x + x + x + ⋯ converges to 2 1 + 4 x + 1 .
Log in to reply
Its easy to show. Y^2=x+y Y^2-y-x=0
Solving with the quadratic formula we get that
Log in to reply
Precisely. I just wanted @Ayon Ghosh to show that himself in his solution. Thank you, Md.
Log in to reply
@Zach Abueg – Yes sir welcome. Ayon you can show that. Its important. And Zach sir, can u suggest me some of the best books to study higher calculus?
Log in to reply
@Md Zuhair – Sure, I'll do my best! How far into calculus?
Log in to reply
@Zach Abueg – I did till beta functions in depth. And those fractional integration. I know bit zeta. So?
Log in to reply
@Md Zuhair – Here's a wonderful paper on integration of fractional part functions.
I agree with that. The proof of the convergence should be included in the solution.
@Md Zuhair Could you please refer some calculus books for me .I have done (limits,continuity,differentiation basic rules,local/global extrema,applications of differentiation,some basic integration techniques till int.by parts and some applications like area enclosed under graph.)Now I want to go for those beta /zeta functions so which book should I go for ?
Log in to reply
I didnt used any book, I used brilliant wiki's. You may try out those. And also, Well done, u r in IXth and u hav finished 12th level calculus! WOW!
I have added the convergence proof. and @Md Zuhair thanks for the suggestion i will start working on it !
observe that
that means,
p = 1 9 and q = 6 thus p − q = 1 3
Since limits are positive we take positive root only in second step.
wrote on latex here