The Distance Length

A B C D is a rectangle with A B = 1 0 , A E = 5 , A C = 6 , and A F = 3 as shown above. Find the length of G H .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
How to do this with simple geometry (without coordinate)?
Log in to reply
I was think about it. Then I gave up.
you can see my solution. Originally i made this prob by using congruence principal. but i think this solution using coordinate bashing is more interesting.
Hope you understand, my solution is in the figure below.
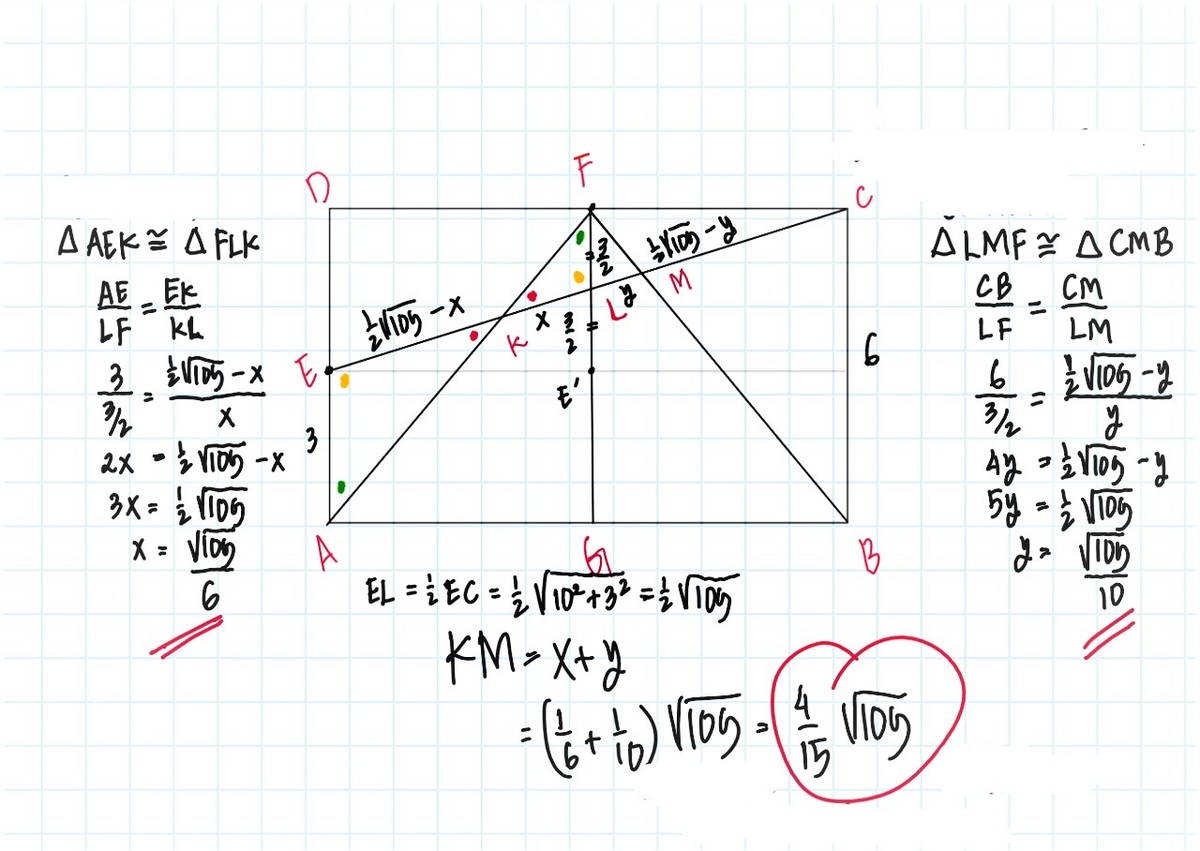
Nice solution! I think ,by mistake, you have used congruent symbol instead of similarity one.
Log in to reply
My mistake, i tend to make a mistakes hahaha
Log in to reply
How did you create this graph and figure?
Log in to reply
@Mr. India – for the figure above i use my pen tablet, as for the figure in the problem i use geogebra/desmos.
Let E be the origin of the x y -plane. The equations of C E , D E , and B F are as follows:
⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎧ C E : D E : B F : y = 5 6 x y = − 5 6 x y = 1 0 3 x − 2 3
Then the coordinates of G ( x G , y G ) and H ( x H , y H ) are:
⎩ ⎪ ⎨ ⎪ ⎧ 5 6 x G = 1 0 3 x G − 2 3 − 5 6 x H = 1 0 3 x H − 2 3 ⟹ x G = − 3 5 ⟹ x H = 1 ⟹ y G = 5 6 ( − 3 5 ) = − 2 ⟹ y H = − 5 6 ( 1 ) = − 5 6
Then we have:
G H = ( − 3 5 − 1 ) 2 + ( − 2 + 5 6 ) 2 = 9 6 4 + 2 5 1 6 = 1 5 4 1 0 9