The easiest IIT JEE Problem.
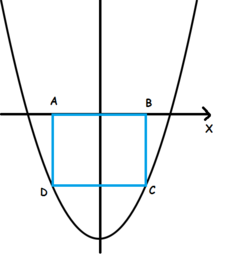 If graph of the expression y =
x
2
- 8x + 12 is shown in the figure then area of the square ABCD inscribed between parabola and X axis is given by:
If graph of the expression y =
x
2
- 8x + 12 is shown in the figure then area of the square ABCD inscribed between parabola and X axis is given by:
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
The diagram suggested my solution: First move the parabola 4 units left so that it's now symmetric about the y-axis(this doesn't change the area of the unique square) , the result of this transformation is x 2 − 4 . If x is half the length of the square and since this square is below the x-axis, we have the equation: x 2 − 4 = − 2 x . We multiply the positive solution by 2 and then square it to obtain the answer.
I thought that the axis of symmetry was the y-axis...oops!
Thank God for multiple choice. I won't learn everything above for another couple of years.
we have to resolve the following problem : given f(x) = x x-8 x+12 , find x1 and x2 / 1) x1< x2 2) x2 - x1 = -f(x1) 3) x2 - x1 = -f(x2) Thus the result is : 24 +8xroot(5)
I don't usually understand this way they explain this posted answers,i need video to make it clearer.
please can someone help me with word problem tutorials.
First of all given figure is completely wrong
Roots of the equation is 2 and 6
When the square is drawn it touches 2 points of the parabola below x-axis
The distance of the point from X-axis be "a", so substitute y=-a in the equation of Parabola
The roots of the equation differ by "a" so using (p-q)= ( p + q ) 2 − 4 p q a quadratic in "a" is obtained
a=-2+2 5
Area= a 2 = 2 4 − 8 5
Well, the figure may be not wrong. The vertical line is not y-axis(at least it doesn't mention). So, I think the vertical line is to show us the symmetry. Who knows? :)
Log in to reply
True Chistopher I know!! Because It's me who Drew the image! Think Well Before You say Something ANIRUDHA! EASY TO FIND WHATS WRONG , HARDER TO FIND WHAT'S RIGHT!!
Log in to reply
good one Sherlock
Log in to reply
@Swapnil Rajawat – That's me! :P
Log in to reply
@Raj Error – Really , you are the second Sherlock Holmes
can you elaborate on p&q you used in equation.
Log in to reply
p and q are the two roots obtained when the quadratic x 2 − 8 x + 1 2 + a = 0 is solved. Essentially, they are the x − c o o r d i n a t e s of the points A and B . So of course, their absolute difference would be equal to the length of the side of the square.
Can you Explain Anirudha Nayak How Is the Figure Wrong ?
I think the figure is WRONG. Because the roots of the equation are 6,2.
Nowhere is it mentioned that the vertical line is the y-axis. Faulty assumptions will lead to wrong answers.
Since the square has equal sides, this infers that the y value of the point at which the curve meets the square equals the x value of the point at which the x-axis meets the square. Hence x = y , or x = x 2 − 8 x + 1 2 , implying that 0 = x 2 − 9 x + 1 2 . Applying the quadratic formula gives the side length of square, from which the area can be found.
We first note, by completing the square, that
y = x 2 − 8 x + 1 2 = ( x − 4 ) 2 − 4
which reveals that the symmetry line of the parabola is x = 4 . Furthermore, y = 0 at x = 2 and x = 6 . A simple graph now shows that the square A B C D is also symmetrical about x = 4 and that point A must lie somewhere in the interval x ∈ < 2 , 4 > and B in x ∈ < 4 , 6 > .
The sides of a square have equal length, so we may conclude that the distance from the symmetry line to point B will be half the distance of B C :
2 ⋅ ∣ 2 1 A B ∣ = ∣ B C ∣ = 2 ⋅ ( x − 4 ) = ∣ y ∣
Since the graph is under the x-axis, ∣ y ∣ = − y , the equation for finding point B becomes
2 ( x − 4 ) = − x 2 + 8 x − 1 2 ⟺ x 2 − 6 x + 4 = 0
which has the solutions are x = 3 ± 5 .
The point B must lie between the values 4 and 6 , so the only option is x = 3 + 5 .
The area of A B C D may now be calculated,
( 2 ⋅ ( x − 4 ) ) 2 = ( 2 ⋅ ( 3 + 5 − 4 ) ) 2 = 2 4 − 8 5