The even consecutive integers
If a , b and c are three consecutive even integers such that a > b > c . What is the value of a 2 + b 2 + c 2 − a b − b c − c a ?
The answer is 12.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Here the one line solution a 2 + b 2 + c 2 − a b − b c − c a = 2 1 [ ( a − b ) 2 + ( b − c ) 2 + ( a − c ) 2 ] = 2 1 [ 2 2 + 2 2 + 4 2 ] = 2 1 [ 4 + 4 + 1 6 ] = 1 2
where did you get the identity?
Log in to reply
Do u need proof ?
Log in to reply
yeah.. also I need to know how you got the values for a,b, and c respectively.
Here is an alternate solution in case you do not understand any of the solutions here:
let the even consecutive integers be 2 , 4 and 6
then, a = 6 , b = 4 and c = 2
then we have,
6 2 + 4 2 + 2 2 − 6 ( 4 ) − 4 ( 2 ) − 6 ( 2 ) = 3 6 + 1 6 + 4 − 2 4 − 8 − 1 2 = 1 2 answer
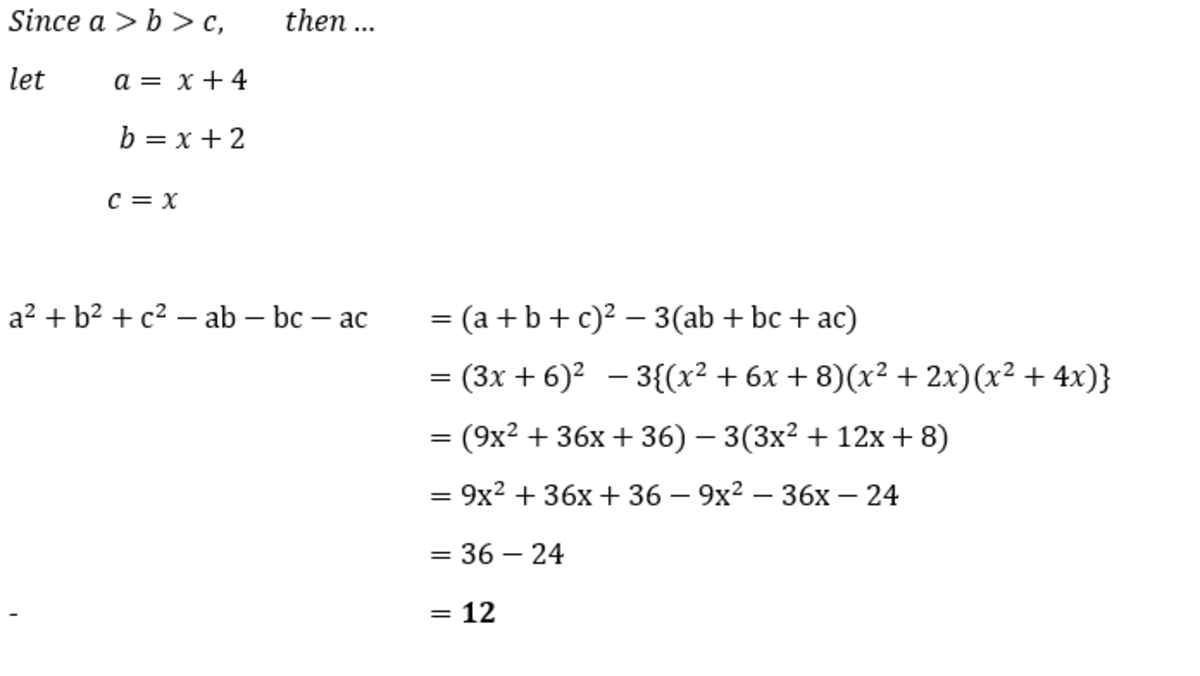
a 2 + b 2 + c 2 − a b − b c − c a = a ( a − b ) + b ( b − c ) + c ( c − a ) = 2 a + 2 b − 4 c = 2 a − 2 b + 4 b − 4 c = 2 ( a − b ) + 4 ( b − c ) = 2 ( 2 ) + 4 ( 2 ) = 1 2