The houses of Nicholas
In Germany, the problem to the right is known as "Das Haus vom Nikolaus." The left diagram is a "house" that can be drawn with a single stroke of a pen (never drawing the same segment twice). A possible solution is on its right.
Which of the diagrams below can be drawn with a single stroke of a pen?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Moderator note:
Patrick Corn mentions it in the comments, but it's worth bringing up here we have a wiki dedicated to Eulerian Paths where you can learn more about this kind of problem.
If I add a node at the center of one of the duplex's "crosses", would an Eulerian path become possible?
Log in to reply
The duplex house has four nodes with an odd number of adjacent edges. An Eulerian path is possible, if the total number of "odd nodes" is either 0 or 2. Just placing an additional node on already existing edges does not reduce the number of "odd nodes". You must add also additional edges, so that "odd nodes" became "even nodes".
An Eulerian path for the duplex house is possible, if you add a new node and (at least) two edges in the right way.
Here is a link to the Eulerian path wiki.
The tower is possible well at least I can do it
Log in to reply
I agree with this as I have managed to do this my self
Log in to reply
can you post the drawing ?
Not very surprising that you agree with yourself, but I will be surprised if you show a diagram with the tower drawn with a single continuous line.
I suspect that you have missed an edge with your mind's eye.
I found a solution to the duplex so I’m confused about this
Log in to reply
If, on the duplex, you label the nodes from left to right, bottom to top so the lower left base of the duplex is node 1 and the top of the right duplex is node 8, A viable solution is
3-2-1-5-3-6-2-4-7-5-8-6-5-4-1
Log in to reply
You're missing the connection between 2 and 5.
I don't agree, I found a solution to the duplex home.
Log in to reply
Me too. The duplex house is definitely possible.
Log in to reply
I would love to see your proof. Either a drawing or an explanation of the moves would be great!
Solution to the duplex: Starting at the bottom right corner, circle the exterior back to the starting point, then up-right, left, down-right, up, and right.
Log in to reply
I'm struggling to follow your instructions. How can you go up-right once you've done a full circle of the exterior when you start at the bottom right corner?
Can you provide a drawing please; or provide a numbering system for the nodes, and then list the steps from node to node - similar to Ivan Berry's system within his comments.
Log in to reply
I'm sorry, i just realized that I stated it wrong. Starting from the bottom LEFT, go up and circle the exterior back to the starting point. This leaves us with only the inner strokes left. Then diagonally up and to the right, then straight left, then diagonally down and to the right, then straight up then straight right. This will work as long as they don't count the inner x's as a part of the "house" - dunno how to post a pic, sorry, maybe cause i'm not a premium member.
Log in to reply
@Andre Munroe
–
You can post a picture that you've uploaded to the internet somewhere (imgur for example) without needing to be a premier user. Use the following structure:
!
[
]
(
h
t
t
p
:
/
/
i
m
a
g
e
u
r
l
)
That's, exclamation mark, square brackets, parentheses with the url inside.
Regardless, I'll try to follow your new instructions tonight (when I'm not at work).
@Andre Munroe – This is what I get following your new instructions.

You cannot draw line 15 .
Log in to reply
@Jonathan Quarrie – Oh i was saying assuming the inner lines don't count. Thought they were just construction lines in order to draw the actual "house". But i guess they are needed
Log in to reply
@Andre Munroe – Yeah, if you don't draw all of the lines, you haven't drawn the diagram.
I have also found a solution for duplex house
Log in to reply
All these solutions claimed for the duplex house, but there is yet to be any proof of an actual solution.
Can you provide a drawing or explain your moves, Amine?
I can prove that all of them can be drawn in just one stroke.
Log in to reply
The tent is the only one of the graphs that can be traced in the manner described because the other two graphs have more than two nodes at which an ODD number of edges meet.
Informally, the reasoning is fairly simple. Consider any node that is neither the beginning nor end of the path you trace. Every time the path enters such a node, it must also exit it. Since the path must travel over every edge once and only once, this implies that every node (other than possibly the beginning and end nodes of the path) must connect an EVEN number of edges. Therefore if there are more than two nodes connecting an ODD number of edges, no path can go over every edge once and only once.
As for the beginning and end nodes, there are two possibilities. Either the path begins and ends at the same node, in which case it, too, must connect an even number of edges; or the path begins and ends at different nodes, in which case those two nodes will necessarily connect an odd number of edges.
Thus, the only graphs that can be traced under the given conditions are ones that have exactly zero or two nodes connecting an odd number of edges.
But I am able to draw the double duplex house with a single stroke by continuing the last line of single duplex house! How do I post an image?
Log in to reply
I think you can publish a solution only if you have the right answer
Log in to reply
And how do I publish a solution? I dont see any option.
Log in to reply
@Pranay Bansal – The option to publish appears only if you have been successful with the answer.
Log in to reply
@Angie Giselle Morocho Alburqueque – Oh. Thanks!
Log in to reply
@Pranay Bansal – Thats lame
Seriously, can you do a solution next time!!!???
All three given examples are graphs. The "Das Haus vom Nikolaus" one is called "Euler's graph". Those ones are able to draw with a single stroke of a pen. A graph is an Euler's Graph in case every knot is connected with an even number of lines or there are two knots which are connected with an odd number of lines. This condition has only one of this figures - the Tent.
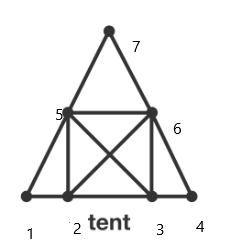
knot 1: 2 lines knot 2: 4 lines knot 3: 4 lines knot 4: 2 lines knot 5: 5 lines knot 6: 5 lines knot 7: 2 lines
There are eight changes in directions in the demonstration.
The tower. You can add unlimited floors to the tower the same way you do with the house, simply mirroring the drawing line.
We search for an trail in a graph, which visits every edge exactly once (Eulerian path). A node, that is neither the start nor end of this trail, must have an even number of adjacent edges. Because, if a node is visited a total of k times, it must have exactly 2 k adjacent edges, so that each edge is visited exactly once. To solve the problem we count for each node of the graphs all adjacent edges:
Each graph has several nodes with an odd number of edges. These nodes would have to be start and end points in an Eulerian path. However, both the "duplex house" and the "tower" have more than two odd nodes, so that an Eulerian path is not possible. For the "tent", however, an Eulerian path can be found, as it has exactly two nodes with odd number of edges.