The Impossible Triangle
A math teacher had drawn on the blackboard a very carefully scaled figure of a triangle divided into six smaller triangles with three straight cuts as follows:
and he proceeded to write in the integer area of each of the six smaller triangles. But as he wrote down the area of the fourth triangle (as shown in this graphic), a bright student raised his hand and said,
"Mr. teacher, but that's wrong, you made a mistake with that number you just wrote!"
The teacher looked at his notes and realized his error, so he rubbed out the last digit of the area of the fourth triangle, put in the correct digit, and then continued to write in the areas for the fifth and sixth triangles.
What was the total area of the big triangle?
The answer is 1320.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Mark, this is wonderful, I've never even heard of the Ladder Theorem. I get up this morning and find this beautifully confirmed. Where did you even find such a theorem? Thank you for bringing it to our attention!
Upvoted!
Log in to reply
It is just a consequence of equations that follow from considering triangles with varying altitudes and bases. For example b a = b + c + d a + e + f d c = d + e + f a + b + c Manipulate these equations, and you get the Ladder Theorem...
Log in to reply
After looking around just now, I see it now. I hadn't thought of using the example of crossed ladders for this one. Let me go play with this a little bit.
Why is the ladder theorem called so?
Log in to reply
In its original form, it concerns the two ladders leaning against opposing vertical walls. An internet search will rapidly give you more information.
I spent a while trying to find a good link: http://2000clicks.com/mathhelp/geometrytrianglecrossedladder.aspx Since length and area are proportional Mark just replaced the lengths with areas
Such a bright student :)
The teacher wrote 2 8 8 when it should have been 2 8 6
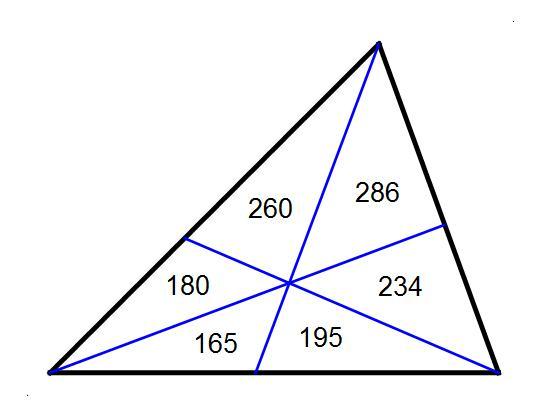
The total of the six areas is 1 3 2 0
In any triangle divided into six smaller triangles with three such straight cuts, the areas of any three smaller triangles uniquely determine the areas of the remaining three smaller triangles, and thus the area of the big triangle.
@Michael Mendrin I couldn't get your hint of the proof.can you please elaborate and include it in your answer.
Log in to reply
I agree with Nikhil. I don't really understand Michael's solution. What he states is correct but how does he solve the problem?
In any triangle divided into six smaller triangles with three such straight cuts, the areas of any three smaller triangles uniquely determine the areas of the remaining three smaller triangles, and thus the area of the big triangle.
Got a proof of this?
Log in to reply
Here's an example, using Mark Hennings' approach, which is to use the Ladder Theorem. By fooling with them, we can come up with the formula for finding the area of, say, triangle f in his graphic
f = b ( a + b ) + c ( b − a ) a c ( a + b )
By similar means, we can find the area of any particular triangle given the areas of 3 others
Oh I'll get around to posting a proof, it's 200 am right now and I can use some sleep. But the gist of a proof lies in the fact that while a triangle with that interior point has 5 degrees of freedom, 2 of them are affine transforms which preserves areas, so that specifying 3 areas already uses up those 3 remaining degrees of freedom. Get it?
Log in to reply
while a triangle with that interior point has 5 degrees of freedom, 2 of them are affine transforms which preserves areas, so that specifying 3 areas already uses up those 3 remaining degrees of freedom.
Degrees of freedom? How is statistics involved here?
Affine transform? This doesn't look trivial to say the least. Can you expand on your explanation?
Log in to reply
@Pi Han Goh – Statistics? How did that word get in there? But all right, I guess i better pull together a proof why it only takes the areas of 3 triangles to determine the rest. One way to do it is to come up 3 equations giving the area of a triangle based on 3 others, as to remove all doubt, but it wouldn't give anyone a "deeper understanding why this is happening"
But I've been kind of busy lately these days. I will try to get to it.
Log in to reply
Statistics? How did that word get in there?
You have clearly written it in your original comment:
Oh I'll get around to posting a proof, it's 200 am right now and I can use some sleep. But the gist of a proof lies in the fact that while a triangle with that interior point has 5 degrees of freedom , 2 of them are affine transforms which preserves areas, so that specifying 3 areas already uses up those 3 remaining degrees of freedom. Get it?
Degrees of freedom article , or are you referencing something else ?
One way to do it is to come up 3 equations giving the area of a triangle based on 3 others, as to remove all doubt, but it wouldn't give anyone a "deeper understanding why this is happening"
Try me.
Log in to reply
@Pi Han Goh – The equations relating a , b , c , d , e , f are ( a + b ) d = ( e + f ) c ( c + d ) f = ( a + b ) e ( c + d ) a = ( e + f ) b Suppose we are told that a = 1 8 0 , c = 2 8 8 , d = 2 3 4 , and we want to find the values of b , e , f . There are three degrees of freedom in this system to the extent that we have three unknown quantities. Since we also have three equations that they must satisfy, we should be able to determine their values (in general, each equation reduces the number of degrees of freedom by 1 , and so the three equations ought to reduce the number of degrees of freedom to zero. In other words, there is no room for uncertainty, and the values of b , e , f are known.)
The problem in this case is that the three equations given above are nonlinear in b , e , f , and so the exact formulae for their solution are horrendous; it is easier to do this sort of problem numerically! In the case I gave above, the values of b , e , f are 2 6 1 . 7 7 1 , 1 9 4 . 4 0 9 , 1 6 4 . 5 3 respectively. Thus we need to look for another trio of values which yield integer solutions...
Log in to reply
@Mark Hennings – Oh woah! Do you know every single thing? Let me see if I can conjure up a complete solution.
@Calvin Lin , every single comment/solution that Mr Mark Hennings made are a gem, please consider sending a notification to everyone everytime Mr Hennings posted a comment/solution.
Log in to reply
@Pi Han Goh – What Mark is saying here is the ladder theorem, or at least the basis of it. However, it's a little more work to show the explicit formulas for all possible Area_a = F(b, c, d), where a, b, c, d are any 4 of the 6 areas.
Do you want those formulas, or the proof that 3 areas determine the rest? Obviously the formulas proves the latter, but the latter shows that the remaining areas are computable given 3 of them.
Mark is right, it can get messy.
@Pi Han Goh – Okay, yes, "degrees of freedom" is something you hear in statistics, but you also hear it in geometry and physics, for example. As an example, consider the set of all triangles. Not counting the location or orientation of triangles in space of any kind, how many variables does it take to define a particular triangle? Just three. In other words, a triangle has three degrees of freedom. How many degrees of freedom does a square have? Just one. How many degrees of freedom does a point have, with respect to any geometrical object, both it and the point on a plane? Two. So, a triangle with an arbitrary point somewhere, inside or out, has a total of 5 degrees of freedom, i.e., it takes "5 numbers" to specify a specific triangle with a specific point inside (or outside) it. In other words, the drawing of the divided triangle shown, without the numbers, has 5 degrees of freedom.
Two of the degrees of freedom doesn't affect the areas. That means if three of the areas are determined, thus taking up the remaining 3 degrees of freedom, then the other three areas are determined.
As an example of how one of the degrees of freedom doesn't affect the area, start with the graphic as posted above, with the areas already in it. Keep the two vertices and that point between them on the bottom line of the big triangle fixed. Then move the apex horizontally, taking with it the 3 lines that meet there. That will move the removing 3 lines. The areas remain unchanged. This is an affine transform.
Two such affine transforms that are independent of each other are possible. That takes up 2 degrees of freedom which doesn't affect the areas.
Any other such affine transforms won't be independent of the first two.
I'll come back to this later with the "proof", once we understand what is meant by "5 degrees of freedom" here. But these days, I'm kind of busy.
Let me do add that I think "degrees of freedom" all the time, both in my math and physics problems. It's a very useful tool. It's kind of analogous to keeping the bookkeeping straight on dimensions of physical quantities.
in the figure there is mistake in the area of 288 ( it should be 286) ..
The Ladder Theorem tells us that a + b + c + d + e + f 1 + e + f 1 = a + e + f 1 + d + e + f 1 where a , b , c , d , e , f are the triangle areas. Similarly, a + b + c + d + e + f 1 + c + d 1 = b + c + d 1 + c + d + e 1
Solving these two equations simultaneously, looking for positive solutions for b , e , in the four cases:
for j = 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 (a total of 4 0 equations - thank you, Mathematica) only gives a positive integer solution for a = 1 8 0 , b = 2 6 0 , c = 2 8 6 , d = 2 3 4 , e = 1 9 5 , f = 1 6 5 , making the total area 1 3 2 0 .