The Internal Angle Bisector

Let AB = c and BC = a. By angle bisector theorem, we have AB/BC = AR/RC = c/a. It implies AR = k c and RC = k a. Say, PR = RQ = x

It's given that: AP + BC = AB + CQ It implies: (AR - PR) + BC = AB + (RC - RQ) ==> (k c - x) + a = c + (k a - x) ==> a (k - 1) = c (k - 1) ... (1)

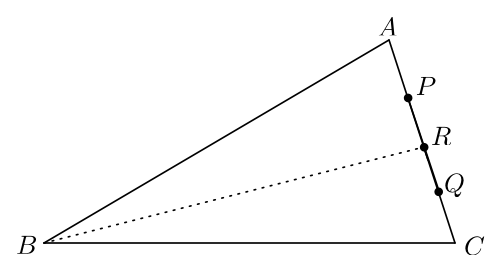If k = 1, then AC = a + c = BC + AB which is NOT the case as BC + AB > AC (Triangle Inequality). Therefore, k ≠ 1 ==> k - 1 ≠ 0 ==> a = c (from equation # 1) ==> AB = BC.

Thus, △(ABC) is isosceles with AB = AC and so, ∠BAC = ∠ACB = (180° - ∠ABC)/2 = (180° - 30°)/2 = 150°/2 = 75°

It's simple triangles BRC & BRA are congruent. So. angles A & B are equal.

Sorry my solution has exactly the same rationale as Shamik's but may give you a better view:

Bisector theorem: $\frac{AR}{AB}=\frac{RC}{BC} \Rightarrow \frac{AP + PR}{AB}=\frac{RQ + CQ}{BC}$ $\Rightarrow \frac{AP + PR}{AB} - 1=\frac{RQ + CQ}{BC} -1$ $\Rightarrow \frac{AP - AB + PR}{AB}=\frac{CQ - BC + RQ}{BC} (1)$

We are given: $AP + BC = AB + CQ \Rightarrow AP - AB = CQ - BC$

Plus $PR = RQ$

Therefore, the numerators on both sides of $(1)$ are equal $\Rightarrow AB = BC \Rightarrow ... answer$

The sum of interior angles of triangle is 180 degrees, the bisector divides the line AC inti 2 equal halves, so those 2 angles are equal, hence the angle will be 75 degree

angle bisector theorem, so the 30 degree is divide into 15 degree to each triangle.... and point R makes 90 degrees to each triangle because of perpendicularity.... so sum of angles inside the triangle is 180 i.e., 15+90+x = 180 x= 180- 105 = 75 degrees

so simple triangles BRC & BRA triangle are congruent. So the angles A & B are equal

Simple Problem, All stories given only to hint that AB and BC are equal(Indirectly), which means angles A and C are equal.
Also A+B+C=180 degrees 2A+B=180 2A+30=180 2A=150 A=75

if an angle bisector bisects at mid point of the the other side then it will be perpendicular and an isosceles triangle. hence divide ( 180-30)/2= 75 degrees

We cannot say right away that the triangle is isosceles we have to prove this to be complete. For that we can use the bisector theorem. Let's assume that AB=a, BC=b, RC=c, AR=d. From the angle bisector theorem we have that a/b=d/c=λ. From the given one can see that a+c=b+d. From the previous two relations we get λb+c=b+λc ==> (λ-1)*(b-c)=0. Hence it comes that {b=c, a=d} or {a=b,c=d}. If {b=c, a=d} then AB+BC=AC which violates the triangular inequaility (AB+BC>AC). Therefore it should be true that {a=b,c=d}, hence ABC is isosceles. From there it is easy to see that <A=<C=(180-<B)/2=75

In <abc if line BR bisecting AC at mid point then right angle triangle is formed <ABR then <ABR =30 and ,ARB=90 add on both these give 105 and subtract it by 180 (total angle of triangle) 180-105=75 degree. ans

Since BR is a angular bisector of angle ABC and it bisects the line AC, the triangle must be an isosceles triangle giving angle BAC ( = angle BCA) equals to (180-30)/2 (=75 degrees).

the angle bisector cuting the base at mid pont,then its a isosceles triangle.angle ARB=90 and RBA=15.sum of the angles in a triangles=>ABR+RBA+RAB=180 =>90 + 15 =RAB=180

                                 =>  RAB=75

it's so easy..

It precisely implies that P & Q are at equilibrium from R and so as A & C which means if provided one angle is given, another two be found then it will be isosceles triangle form two other sides.

As in one and is given 30 degree and another two similarly are 75 degrees

the sum of angles in triangle is 180 now x+y+30=180,x=y from given conditions so 2x+30=180 gives x=75

75

There is no need of AP + BC = AB + CQ. Since the angular bisector meets the midpoint of the opposite side, it divides the triangle into two congruent triangles, hence AB=AC, therefore ∠BAC = ∠ACB = 75°

Let angle ABC = 30 ; angle ARB= 90 , ( A | C mid point ) and anlgle ABC/2 (Bisector of ABC),

30/2 =15, angle ABR=15 , ARB=90, angle ARB+ABR+BAR=180, 15+90+BAR=180,
angle BAR=180-105 = 75,

m<R 90 degrees, the m<B is 15 degrees, the total measure of angles in a triangle is 180 degrees, therefore 90+15=105, 180-105=75 so the m<BAC is 75 degrees.

sum of angles in triangle =180 <a+<b+<c=180 <a+<a=150 <a=150/2=75

since triangle is isosceles so angle is 75

Let AB = c and BC = a. By angle bisector theorem, we have AB/BC = AR/RC = c/a. It implies AR = kc and RC = ka. Say, PR = RQ = x

It's given that: AP + BC = AB + CQ It implies: (AR - PR) + BC = AB + (RC - RQ) ==> (kc - x) + a = c + (ka - x) ==> a(k - 1) = c(k - 1) ... (1)

If k = 1, then AC = a + c = BC + AB which is NOT the case as BC + AB > AC (Triangle Inequality). Therefore, k ≠ 1 ==> k - 1 ≠ 0 ==> a = c (from equation # 1) ==> AB = BC.

Thus, △(ABC) is isosceles with AB = AC and so, ∠BAC = ∠ACB = (180° - ∠ABC)/2 = (180° - 30°)/2 = 150°/2 = 75°

iSCOSCELES tRIANGLE PROPERTY..!!!

First of all Find the Value of angle A and angle C . like :- angle B is 30 degree given, Remain Degree is (180-30)/2=75 each angle for angle A And angle C; Given that AP+BC = AB+CQ mid value is R to makes new angle is 90 is both of tringle which is the tringle ARB = tringle CRB Angle R=90 so angle of A is angle A + angle R + Angle B = 180 degree Angle A = 180-(Angle R+Angle B) Angle A = 180-(15+90)=180-105=75 Degree. So, Angle of A is 75 Degree

Since segment BR bisects the 30 degree given angle and that Point R is the midpoint of the side opposite to the given angle, segment BR is therefore a perpendicular bisector. It forms two right triangles: BRC and ARB .

Taking triangle ARB to solve for Angle A, we take the value of angle B/2 = 15 degrees and add it up to the 90 degree angle formed by segment BR to segment BC and subtract it to 180 degrees, which is the sum of all angles in a triangle .

Angle A = 180 - (Angle B/2 + 90 degrees) = 180 - (15 degrees + 90 degrees) = 180-105 Angle A = 75 degrees .

here two side's of tringle is eqals so it is isoleteral tringle so rest of two angle is also eqal so solution is 75degree

R is mid point of AC so R is median of triangle ABC. it will intersect AC at 90 degree. ABC is of 30 degree and ABR is 15 degree. IN triangle ABR,
angle ABR+angle ARB+angle BAR=180 15 + 90 +angle BAR=180 angle BAR=180-105=75 R is mid point of AC ,, so angle BAC=75

from question we have the distance AP=QC and hence AB=BC then angle of A=angle of c since angle( A+C)=180-angle of B that is 30 hence angle A=75

since R is the bisector of P&Q as well as A&C ,therefore AP=QC.Resulting AB=AC and making triangle isosceles.so applying angle sum property of triangle we can find out the angle

1. Angle ABC = 30 degrees - We all know a triangle always has 180 degrees, so 180 - 30 = 150 degrees.
2. Divide 150 with 2 = 75 degrees.

=>ABR=30/2=15; =>A+15+90=180 ; (ARB=90) Hence A=75

AP=QC AP+BC = AB+CQ BC=AB Therefore , Triangle ABC = Iscoceles Triangle with AB=BC Angle bac = Angle acb 30+angle bac+ angle acb=180 angle bac= 150/2 = 75

since the angle bisector divides the given angle 30 into 2 . then it will become 15. angle bisector usually forms a right angle which is 90. simple math, 180=x+15+90.. find for x. you will be able to get the answer as 75.

SINCE R IS THE MIDPOINT THEREFORE IT IS PERPENDICULAR. SO ANGLE ABC SHOULD ALSO BE BISECTED. SO ANGLE ABR IS 15. SO ANGLE BAC = 180 - (90+15) = 75 DEGREES

here, BR is a median because it is 90 degrees (as it is a perpendicular bisector) and in triangle ABR, angle ABR = 1/2 of ABC so, 15 + x + 90 = 180 or x = 75 where x = unknown angle