The King (still) needs your help
An ambitious king plans to build five new cities in the wilderness, connected by a network of roads, so that any city can be reached from any other. He expects the annual tax revenues from each city to be numerically equal to the square of the population. Road maintenance will be expensive, though; the annual cost for each road is expected to be numerically equal to the product of the populations of the two cities that road connects. The project is considered viable as long as the tax revenues exceed the cost, regardless of the populations of the various cities (as long as at least one city has any inhabitants at all). How many options does the king have, that is, how many graphs (up to isomorphism) can he use to get a viable layout, with the vertices representing the cities and the edges representing the roads?
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Thank you, Abhishek... you have all the right ideas.
As you say, we can easily "complete the squares" to show that the revenue-cost functions q of Raghav's two graphs are positive definite.
In the case of the path graph on the left, with populations a 1 , a 2 , . . . , a n , we have q ( a 1 , . . . , a n ) = 2 1 ( a 1 2 + ∑ k = 1 n − 1 ( a k − a k + 1 ) 2 + a n 2 ) which is positive unless all populations are zero.
In the case of the graph on the right, label the populations at the two "leaves" on the right b and c and the others a 1 , a 2 , . . . , a n , with a 1 being the population of the city with three neighbours. Then q ( a 1 , . . . , a n , b , c ) = 2 1 ( ∑ k = 1 n − 1 ( a k − a k + 1 ) 2 + a n 2 ) + ( b − 2 a 1 ) 2 + ( c − 2 a 1 ) 2 , which, again, is positive unless all populations are zero.
Actually, there are three types of trees on five vertices. Can you find the third type and show that it isn't viable?
FOLLOW-UP QUESTION: Besides the two types of trees discussed here, are there any other trees, on any number of vertices, that lead to a viable plan?
Log in to reply
The third one is a star graph : one node in the middle and 4 other nodes directly attached to the middle one. To show infeasibility consider the following configuration : 2 people in the middle node and 1 person each in other nodes. Total revenue : 2 2 + 1 2 + 1 2 + 1 2 + 1 2 = 8 . Total cost = 4 × 2 = 8 . Hence infeasible.
Log in to reply
Exactly! We are done with this one... I just posted another.
Besides the two types of trees discussed here, are there any other trees, on any number of vertices, that lead to a viable plan?
Yes, there are.
Taking Raghav's right tree as a starting point, you could extend the longest branch to any desired length and it would still be a viable plan. Or you could instead extend one of the other two branches by three and it would still be a viable plan. Or you could take any (connected) sub-tree of any of those (including, naturally, a straight chain of any desired length).
Log in to reply
Sounds good! Thanks! So, how many graphs are there besides the "path graph" of arbitrary length and the "two-pitched fork" with an arbitrarily long handle? And why is all that true? See this
Log in to reply
See this
Thanks. I see now that this discussion is older than I had previously realized. (I guess I could have saved myself a bunch of work if I had visited those other 2 problems earlier -- but then again, easier often means less interesting. :) )
WIth OEIS sequences, I believe that they tend to index by 0 where possible (even if it gives a trivial value).
Log in to reply
Yes, that confused me a bit. Should have double-checked it.
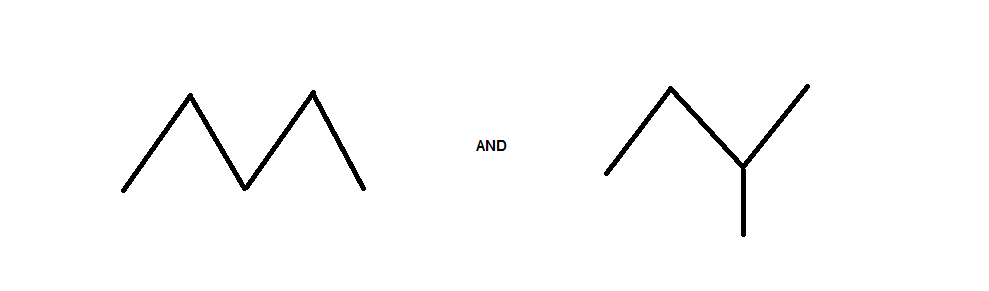
Where each vertex of the graph is a city. Don't ask me why.
You are correct! Thanks! I have to ask "why?" though ;)
Log in to reply
Actually, what happened was that I guessed 2. I knew that the straight chain was a solution(courtesy of your explanation in previous problem). Then I thought there might be one more. Once the answer is known to be 2, it is easy to prove that these two must be the viable options. But otherwise, I am lost.
Log in to reply
Let's wait a while to see whether anybody else comes up with a solution. If not, I guess it will be my turn.
First note that a viable network can not contain cycles. Because if a connected graph on n vertices contains a cycle (i.e. it is not a tree), then it has at least n number of edges (roads). Then consider the case when every city has exactly one person. Then, we have revenue = n and total cost ≥ n , resulting in infeasibility.
Hence the viable network must be a tree. Now with n = 5 vertices, there are only two distinct trees (upto isomorphism). These two trees are as drawn in Raghav's answer. One can just try to prove the result by trial and error or look up here .
To show that these two graphs indeed satisfy the constraints consider the inequality ∑ ( i , j ) ∈ E ( n i − n j ) 2 ≥ 0 , for the first graph and something similar for the second graph. Here E denotes the edges and n i denotes number of people on node i .
EDIT : As Otto mentioned, there is another tree, the star graph. It can be shown to be infeasible. Please see my comment below.