The Lightning Scar

Geometry Level 3

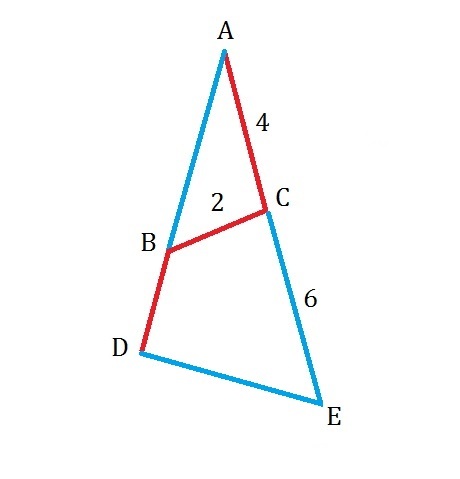
Long after Voldemort's defeat, Harry Potter, now a specialized and well-known Auror, just discovered that his lightning scar (marked red) was, in fact, a part of another symbol for the fourth Deadly Hallow: the Congruence Spear, which could usurp the magical power from whomever it killed.

The segments $AC$ , $CB$ , & $CE$ are measured $4$ , $2$ , & $6$ respectively as shown above, and the new mark(blue) is constructed such that the $\triangle ABC$ is similar to the $\triangle AED$ with $AB + BC = BD + DE$ .

If $AB = x$ ; $BD = y$ ; and $DE = z$ for some numbers $x, y, z$ , what is the value of the 3-digit integer, $\overline{xyz}$ ?

Image Credit: Harry Potter & the Prisoner of Azkaban.

The answer is 534.

1 solution

Worranat Pakornrat
Mar 29, 2016

Since the $\triangle ABC$ is similar to the $\triangle AED$ , we can equalize the ratios of the side lengths as followed:

$AB : BC : CA = AE : ED : DA$

$x : 2 : 4 = 10 : z : x + y$

And we know that $AB + BC = BD + DE$ , so $x + 2 = y + z$ . $y = x - z + 2$ .

Thus, $x : 2 : 4 = 10 : z : 2x - z + 2$ .

This can be rewritten as:

$\dfrac{10}{x} = \dfrac{z}{2} = \dfrac{2x - z + 2}{4}$

Solve for $z$ in terms of $x$ in the first half, we will get $z = \dfrac{20}{x}$

Substituting $z$ in the other equation, we will get:

$\dfrac{10}{x} = \dfrac{2x - \dfrac{20}{x} + 2}{4}$

$40 = 2x^2 - 20 + 2x$

$0 = 2x^2 + 2x -60$

$0 = x^2 + x - 30 = (x - 5)(x + 6)$

Hence, $x = \boxed{5}$ .

$z = \dfrac{20}{5} = \boxed{4}$ .

And $y = 5 - 4 + 2 = \boxed{3}$ .

As a result, $\overline{xyz} = 534$ .

Moderator note:

Great write-up.

When dealing with a geometric scenario and converting it into algebra, we should check that the final answer makes sense. For example, we need lengths and areas to be positive (unless we're using directed lengths/areas), and for triangles to satisfy the triangle inequality. In a previous version of this problem, the triangle ended up being a straight line.

Triangle ABC is similar to AED and not ADE. If you solve it that way then we get the answer. Do you want us to figure out what the question is? BTW I solved the question but it was dissaponting.

Kushagra Sahni - 5 years, 2 months ago

What do you mean ABC is similar to AED but not ADE?

Worranat Pakornrat - 5 years, 2 months ago

Are you aware of the order in which we write the triangle vertices? Or do you think that even if we write DAE or any of the 6 combinations it means the same. ABC being similar to AED means that Angle ABC equals AED, Angle ACB equals ADE and BAC equals EAD. We take the vertices in the same order in both triangles. That's the way to write.

Kushagra Sahni - 5 years, 2 months ago

@Kushagra Sahni – OK, I'll change it to AED then.

Worranat Pakornrat - 5 years, 2 months ago

I already changed the question details. Now it should be a triangle while the answer is still the same.

Worranat Pakornrat - 5 years, 2 months ago

Great! This is an interesting problem where the values are kept small and we can "somehow" find the lengths to meet the criteria.

Calvin Lin Staff - 5 years, 2 months ago

also he isn't an auror, he is head of a department

Bách Hữu Trần - 1 year, 2 months ago

The Lightning Scar

Image Credit: Harry Potter & the Prisoner of Azkaban.

The answer is 534.

1 solution

Moderator note:

0 pending reports