The Midpoint Of The Points Of Tangency
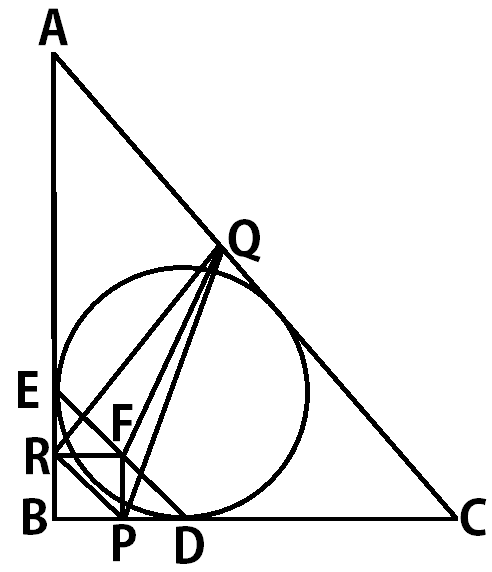 In right angled
△
A
B
C
,
∠
A
B
C
=
9
0
°
and
∠
B
C
A
=
6
0
°
. The incircle of
△
A
B
C
touches sides
B
C
and
A
B
at points
D
and
E
respectively. Let
F
be the midpoint of
D
E
.
P
,
Q
,
R
are the feet of perpendiculars from
F
on
B
C
,
C
A
,
A
B
respectively. Let
k
=
P
Q
+
Q
R
+
R
P
A
B
+
B
C
+
C
A
. Find
⌊
1
0
0
k
⌋
.
In right angled
△
A
B
C
,
∠
A
B
C
=
9
0
°
and
∠
B
C
A
=
6
0
°
. The incircle of
△
A
B
C
touches sides
B
C
and
A
B
at points
D
and
E
respectively. Let
F
be the midpoint of
D
E
.
P
,
Q
,
R
are the feet of perpendiculars from
F
on
B
C
,
C
A
,
A
B
respectively. Let
k
=
P
Q
+
Q
R
+
R
P
A
B
+
B
C
+
C
A
. Find
⌊
1
0
0
k
⌋
.
Details and assumptions
-
⌊ x ⌋ denotes the greatest integer function, i.e. it is the greatest integer not exceeding x . For example, ⌊ 2 . 3 ⌋ = 2 , ⌊ π ⌋ = 3 , ⌊ 5 ⌋ = 5 .
-
Once you find the exact form of k , you might use a calculator to proceed.
-
The last digit of the answer that is being accepted is 8 . If your answer slightly differs from the intended one because of approximation errors, you should enter the closest integer whose last digit is 8 .
-
GeoGebra users will be prosecuted.
The answer is 268.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
It is a very tedious question.I practically gave up after using the Pythagoras theorem, because I knew it would be a long grind.Although this question was nice,and given your age, you are well beyond your years,I would encourage you to look into questions with more elegant answers. Anyways, good going buddy,your knowledge is frighteningly impressive.
Directly using coordinates and analytical geometry gives a slightly alternative solution, and it is not longer than this one. Anyway, the question is quite tedious and not elegant at all.
You must check your soln, As, co-ordinate of D-->({sq rt\3-1}/2,0) and of E-->(0,{sq rt\3-1}/2)
Log in to reply
Oh yeah, that's another typo! Fortunately that doesn't matter because that leaves the coordinates F unchanged.
Tedious. V tedious.
Very long calculations and processes
but k = (AB+BC+CA)?(PQ+OR+RS) right?
Just call one side of ABC as J, then find the other sides of ABC. After this find the radium of the circumference depending on J. Finding the radium you can find all the measures with pytagoras. A tip is putting a value to J, your choice, it wont make a difference. Abuse of your calculator =D.
Here's a slightly easier method: Assume AC = 8b, BC=4b & AB=4√ 3 b. AB is: x/(4b)+y/(4√ 3 b) = 1. Slope AC= -√ 3. Let FQ be: y= - x/√ 3 + k. We know that r=(AB+BC-CA)/2, from which midpoint F is [(b√ 3 -b),(b√ 3-b)]. FQ passes through this point so we get k= -2b + b√ 3 - b/√ 3 and therefore, FQ is: y = x/√ 3 - 2b + b√ 3 - b/√ 3 . Determine the intersection of this line with AC which is: x/(4b)+y/(4√ 3 b) = 1 as above. We find Q:[(√ 3/2+2)b, (2√ 3- 3/2)b] whereas P:[2(b√ 3 -b),0] & Q:[0,2(b√ 3 -b)]. Now it's only a matter of calculating PQ, QR & RP using the distance formula and finding the total to be 7.0054948b while AB+BC+CA=8b+4√ 3 b+4b = 18.78057b which gives k~=2.68.
The correct answer is 238.44746
I did it slightly differently, though as long. I used cosA + cosB + cosC = 1 + r/R. Assuming the length of the hypotenuse to be x, R=x/2 (right angled triangle), finding a bunch of angles and a very focused mind, you should end up with 268 :)
Log in to reply
Could you show your method? I can't see how you'd continue from there.
the best way to solve this type of problem is by construction using any CAD tools.Does not take much time either
Log in to reply
As I mentioned in my problem, GeoGebra or any other drawing tools are prohibited.
This is very wrong solution.
the right R is
B D = ( A B + B C + A C ) / 2 − ( A E + C G )
B D = ( A B + B C + A C ) / 2 − ( A E + ( A C − A E ) )
B D = ( A B + B C − A C ) / 2 − ( A C )
B D = ( A B + B C − A C ) / 2
Log in to reply
Typo. Fixed!
Log in to reply
not only there are typos but your whole solution is wrong.
Log in to reply
@Shahbaz Patel – No it isn't. Care to elaborate? Also, note that GeoGebra agrees with me.
We start by computing the lengths of B D and B E . Let the incircle touch A C at G . Since A B , B C , C A are all tangents to the incircle, B D A E C D = = = B E A F C F Note that B D + D C B E + E A A F + F C = = = B C A B A C Summing them up, ⟹ 2 ( B D + C G + A E ) B D + C G + A E = = A B + B C + C A 2 A B + B C + C A Now, B D = = = = B D + C G + A E − ( B D + C G ) 2 A B + B C + C A − ( B D + C D ) 2 A B + B C + C A − A C 2 A B + B C − C A
Now, instead of computing the lengths P Q , Q R , R P , we shall find out the lengths of A F , B F and C F . Let B C = a . Then, A B = a tan 6 0 ° = 3 a and B C = cos 6 0 º a = 2 a . Set the Cartesian coordinates B = ( 0 , 0 ) , C = ( a , 0 ) , A = ( 0 , 3 a ) .
We have B D = 2 A B − B C + C A = 2 3 a − a + 2 a = 2 3 + 1 . It follows that the coordinates for D are ( 2 3 + 1 a , 0 ) . Similarly, the coordinates for E are ( 0 , 2 3 + 1 a ) . Using Section rule, we find out that the coordinates of F are ( 4 3 + 1 a , 4 3 + 1 a ) . Computing the lengths A F , B F and C F is a straightforward job now. A F B F C F = = = = = = ( 4 3 + 1 a ) 2 + ( 4 3 + 1 a − 3 a ) 2 2 8 − 3 a ( 4 3 + 1 a ) 2 + ( 4 3 + 1 a ) 2 2 2 3 + 1 a ( 4 3 + 1 a − a ) 2 + ( 4 3 + 1 a ) 2 2 4 − 3 a
Since ∠ A R F = ∠ F Q A = 9 0 ° , quadrilateral A R F Q is cyclic with diameter A F . By sine rule on △ A R Q , sin A R Q = A F . Also notice that A C is the diameter of the circumcircle of △ A B C , since ∠ A B C = 9 0 ° . By Sine rule on △ A B C , sin A B C = A C = 2 a . Eliminating sin A , we find out that R Q = 2 a A F × a = 2 A F = 4 8 − 3 a . Similarly, we find out that P Q = 2 3 × 2 4 − 3 a and P R = 2 2 3 + 1 a .
k = A B + B C + C A P Q + Q R + R P = 3 + 3 4 8 − 3 + 2 3 × 2 4 − 3 + 2 2 3 + 1 ≈ 0 . 2 6 8 Our desired answer is ⌊ 1 0 0 k ⌋ = 2 6 8 .