There must be a pattern here!
[ ( x + y ) ( x + z ) + ( y + z ) ( 2 y ) ] + [ ( x + 2 y ) ( x + y + z ) + y z ]
Let x , y , and z be real positive number, such that x + 2 y + z = 9 . Find the maximum value of the expression above.
Hint: Two inequalities are summed up.
For more problem on finding maximum and minimum value, click here
Try another problem on my set! Warming Up and More Practice
The answer is 18.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Fidel Simanjuntak Good solution! Anyways, it should be "There must be a pattern here!".
By the way, I see a few typing errors. Can you please fix them?
Log in to reply
Edited. Thanks for pointing it out! What do you think about this set of problems?
Log in to reply
A good one, not 2 hard but not 2 easy. That's what I expect in such a set.
By the way, it's "Hence, the answer..."
Log in to reply
@Steven Jim – Oh my goodness .. Hahahahaaa,, thanks for pointing it out..
Log in to reply
@Fidel Simanjuntak – It's okay :)
Log in to reply
@Steven Jim – What problem do you like at most?
Log in to reply
@Fidel Simanjuntak – "K gives a great inequality" is a good one.
Log in to reply
@Steven Jim – Wew.. I like it too..
Log in to reply
@Fidel Simanjuntak – Yeah. And I feel like others are somewhat easy to guess.
@Fidel Simanjuntak – By the way, try this set.
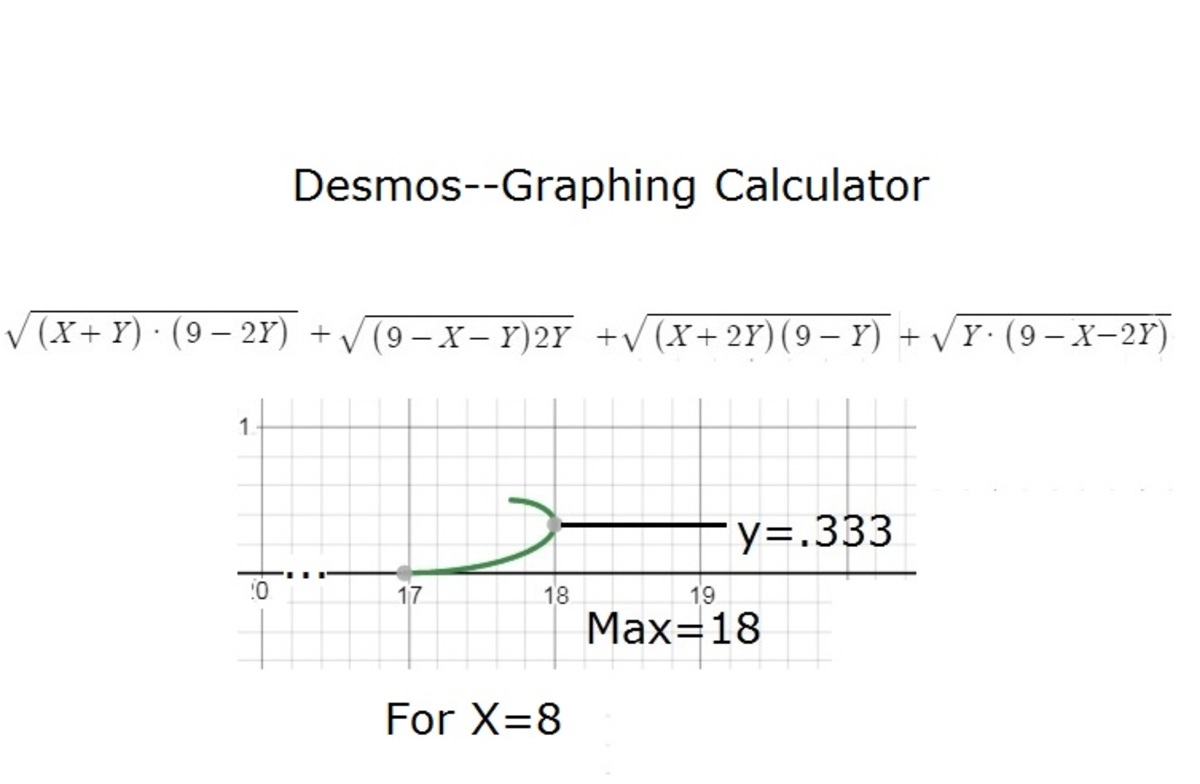 Plotting the graph, taking z=9-x-2y, and vari\ying x=1 to 10, after which y goes to <0. The max of curve stay near 18 for many values.
Plotting the graph, taking z=9-x-2y, and vari\ying x=1 to 10, after which y goes to <0. The max of curve stay near 18 for many values.
With Cauchy-Schwarz Inequality, given a c + b d ≤ ( a + b ) ( c + d ) .
First, let a = x + y ; b = y + z ; c = x + z ; d = 2 y
Then, we have
( x + 2 y + z ) ( x + 2 y + z ) 9 ≥ ( x + y ) ( x + z ) + ( y + z ) ( 2 y ) ≥ ( x + y ) ( x + z ) + ( y + z ) ( 2 y ) . . . ( 1 )
Second, let a = x + 2 y ; b = z ; c = x + y + z ; d = y
Then, we have
( x + 2 y + z ) ( x + 2 y + z ) 9 ≥ ( x + 2 y ) ( x + y + z ) + ( z ) ( y ) ≥ ( x + 2 y ) ( x + y + z ) + y z . . . ( 2 )
( 1 ) + ( 2 ) gives
[ ( x + y ) ( x + z ) + ( y + z ) ( 2 y ) ] + [ ( x + 2 y ) ( x + y + z ) + y z ] ≤ 1 8
Hence, the answer is 1 8