The not-so-hard-working flights
In the country of Brilliantia, there are n > 6 0 airports built recently such that the distances between any two airports are all different from one another.
A plane will always fly from an airport to the nearest airport. Let an origin of an airport A be another airport that flies planes to A .
What is the maximum number of origins an airport can have?
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
An interesting thought is whether this proof holds up on a spherical planet, rather than a flat planet. It does, because on a spherical planet, triangle have angles whose sums are greater than 180 degrees.
Log in to reply
The proof still holds on a spherical planet, since you look at a very small patch that looks like a plane.
Now if we talk about hyperbolic geometry, where angles of a triangle sum to less than 1 8 0 ∘ , we can possibly get a higher answer. It depends on the surface.
Log in to reply
It is well known that an hexagonal tesselation is the most effective way to cover a plane. Therefore, if the airports are located at the vertices of an hexagonal tesselation, the optimum regular separation between airports is achieved. Therefore, the maximum number of airports closest to a given one is k< 6 and the solution has to be 5 (as you explain very well). This reasoning can be easily generalized to spheres (as suggested by Sean). In this case the hexagonal tesselation is not possible and the best solution is the so called spherical polyhedron (composed of hexagons and pentagons). Therefore, over an sphere, the solution should be 4.
Log in to reply
@Jose Jimenez – Sorry for my comment regarding the sphere, it is an error. In fact, the solution is 5 as well. Since the tesselation is a spherical polyhedron, it can happen that the optimum is strictly <6 in for some airports (those that correspond to the hexagons) . Therefore, 5 is also the solution for the sphere. In any case, it is less likely (more difficult to achieve), but still possible.
Log in to reply
@Jose Jimenez – Very fascinating. I've never thought of that. You get an applause from me!
Your solution assumes that the airports are all located on a common plane. If we assume mountainous terrain, we open up another degree of freedom; at the extreme case (very steep mountains/valleys) the airports could be located on the surface of a spheroid, with Airport A located about half-way up a mountain In this case it is possible to have more than 5 origins.
Log in to reply
Well, have fun solving that out! Also, because of extreme weather conditions, there're not a lot of airports open on the mountains.
Fair enough. It's not listed in the problem, but I assume that the country is located on a plane with no mountainous terrain or anything.
With mountainous terrain, the equivalent formulation would be placing this in three dimensions. If there are points in three dimensions and from each point we look at the closest neighbor, what is the maximum number of times a point can be looked at?
Log in to reply
That's interesting. You can't go through mountains, and you can't put airports on mountains (as I mentioned before). Somehow this problem became, rather a discussion.
I've deleted the line: "Every plane takes off and lands at the same time." so the probability will be a lot smaller but it's still possible.
I KNEW it had to have a 5. I've been out of school for too long to get it done properly anymore :(
Ivan's solution is based in geometry, but this is also a theorem of weighted graphs. A nearest-neighbor graph is the directed graph obtained from a weighted graph by connecting each vertex to its nearest neighbour. If the original graph is in general position (so that all distances between vertices are different), this is a planar graph with each vertex having valency at most 5 .
But, isn't the proof of the theorem the geometrical argument?
Log in to reply
I did not buy the paper. The abstract talks about NNGs in abstract metric spaces. If the theorem is valid in other metric spaces than Eucludean ones, then the geometric proof is not enough.
Not a strict proof , Just a way to 'get' the answer
If we have two airports:
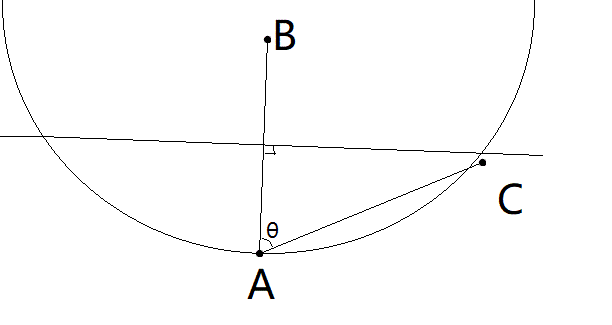 and suppose A is the one that has most 'origin'
So , when we add the third airport (which is a origin of A) to the country,It can't be located in the circle , or above the line. That means θ will always be less than 60 degrees. One by one we add other airports (origins of A) to the country, they are all supposed to have a θ bigger than 60 degrees.
Their sum can't be greater than 180° , So the origins of A should be less than 6 , wich is 5.
and suppose A is the one that has most 'origin'
So , when we add the third airport (which is a origin of A) to the country,It can't be located in the circle , or above the line. That means θ will always be less than 60 degrees. One by one we add other airports (origins of A) to the country, they are all supposed to have a θ bigger than 60 degrees.
Their sum can't be greater than 180° , So the origins of A should be less than 6 , wich is 5.
if a plane always flies to the nearest airport, then after its first flight , the nearest airport is the one he just came from. therefore the maximum number of origins is 2, because he can never go anywhere else.
Consider three airports A , B , C . Suppose A B is the longest side; we claim that no flight goes between A B . But this is trivial to see: a flight from A will never choose B , since C is closer (and probably some other city is even closer, but basically not B ), and likewise a flight from B will never choose A . Thus any pair of cities that is the longest side of some triangle can be immediately ruled off.
Suppose a city A receives flights from the set of cities S . We claim that for any two cities B , C ∈ S , we have ∠ B A C > 6 0 ∘ . This is easy to see, by remembering that the longest side of a triangle is always opposite the largest angle. Since there are flights along the pair A B and A C , this means B C is the longest side, and hence ∠ B A C is the largest angle. But if ∠ B A C ≤ 6 0 ∘ , this means we have the other two angles ∠ A B C , ∠ A C B < 6 0 ∘ . Their sum is less than 1 8 0 ∘ , contradiction.
Now that angles between two cities in S is greater than 6 0 ∘ , simply sweep clockwise around A . It will meet every city in S once before returning to its original position; suppose we call the elements S 1 , S 2 , S 3 , … , S k in order met (and after S k , we continue until it meets S 1 again). Then ∠ S i A S i + 1 > 6 0 ∘ for all i (with S k + 1 = S 1 ). Adding everything up gives 3 6 0 ∘ > k ⋅ 6 0 ∘ , so k ≤ 5 . This is easily achievable.