The Orbits' Envelope of the Projectiles
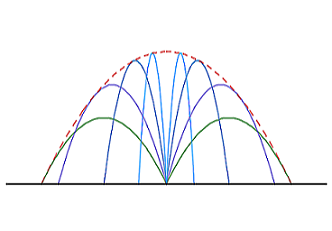
Suppose at initial height 0 , one casts a projectile into the air with constant initial velocity v but different elevation angles in the same vertical plane. The area of the set of all points that can be reached by the projectile is A = α g 2 v 4 . What is the value of positive number α ?
Neglect air resistance.
The answer is 0.6666667.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Alternatively One notes That the equation of the envelope of all projectiles is. Y=v^2/2g - gx^2/2v^2 (At a given x,what is the maximum y one can achieve) We integrate the area under y(x) With limits being from -v^2/g to +v^2/g (The limits correspond to the extreme horizontal ranges of the projectiles)
Log in to reply
How would we derive the envelope, Suhas?
Log in to reply
Take the trajectory equation
y = x tan θ − 2 v 2 g x 2 sec 2 θ
Differentiate with respect to θ :
0 = x sec 2 θ − v 2 g x 2 sec 2 θ tan θ
Now eliminate θ from these equations.
That is not what the question asked. It asked for an area. You wanted a volume.
The trajectory of a projectile with fixed initial speed but variable angle is given by
y t r a j = x tan θ − 2 v 2 cos 2 θ g x 2
The envelope of the family of trajectories are the set of all points reachable by all the trajectories, and must satisfy the condition that the envelope function y ( x ) must be tangent to and contain the point (x,y) at all points that intersect with a trajectory.
This is satisfied when F ( x , y , θ ) = x tan θ − 2 v 2 cos 2 θ g x 2 − y = 0 and ∂ θ ∂ F ( x , y , θ ) = x sec 2 θ − v 2 cos 2 θ g x 2 tan θ = 0 .
Combining the two gives the envelope function to eliminate terms with θ gives
y = 2 g v 2 ( 1 − v 4 g 2 x 2 ) .
We recognize h = 2 g v 2 and R = g v 2 as maximum height and maximum range.
If we go to unitless so that v = y / h and u = x / R and agree to scale areas by a factor h R = 2 g 2 v 4 then the area required by the question is easily found by:
A r e a = h R ∫ − 1 + 1 ( 1 − u 2 ) d u = h R ( 2 − 2 / 3 ) = 4 / 3 h R = 3 2 g 2 v 4
Thus, the answer is 2 / 3
Nice solution bro
The trajectory for a particle projected at an angle of θ to the horizontal is y = x tan θ − 2 v 2 g x 2 sec 2 θ Let us write d = g v 2 . Then the maximum height that can be reached by the particle (when θ = 2 1 π ) is 2 1 d , and the maximum range of the particle (when θ = 4 1 π , 4 3 π ) is d . If we consider the curve C given by the equation y = 2 d 1 ( d 2 − x 2 ) then 2 d 1 ( d 2 − x 2 ) − ( x tan θ − 2 d 1 x 2 sec 2 θ ) = 2 1 d − x tan θ + 2 d 1 x 2 tan 2 θ = 2 d 1 ( x tan θ − d ) 2 Thus the curve C always lies above every trajectory curve, and touches the θ trajectory at the point x = d cot θ . In other words, C is the envelope of the trajectories. The area between C and the x -axis is easy to calculate as 3 2 d 2 , and hence α = 3 2 .