The Other Way Around
a + b + c a 2 + b 2 + c 2 a 3 + b 3 + c 3 = = = 1 2 3
Numbers a , b , c satisfy the equations above.
What is the value of a − 1 + b − 1 + c − 1 ?
The answer is -3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
An alternate (slower) way to derive the answer is by finding the values of a + b + c , a 2 + b 2 + c 2 , a 3 + b 3 + c 3 in terms of a + b + c , a b + b c + c a , a b c by Newton Sums Method, then solving for those three expressions, which is what I did.
This basically just reproves the identities you used though. (I can never remember those Algebraic identities!)
Log in to reply
what is newton sums method @daniel liu
Log in to reply
See here
Log in to reply
@Daniel Liu – It's still incomplete though. I can't seem to get enough time to complete it. The school projects are a pain in the arse. :P
@Daniel Liu I corrected a typo in there, I think that's why you're wondering where those identities come from. It was just basically derived from Newton-Girard formulas.
@John Obia: No actually formula for 3abc = (a+b+c)[(...) ] hasa typo maybe.
Log in to reply
It must have been overlooked.
(
a
+
b
+
c
)
3
=
a
3
+
b
3
+
c
3
+
6
a
b
c
+
3
(
a
2
b
+
a
2
c
+
a
b
2
+
b
2
c
+
a
c
2
+
b
c
2
)
So
a
3
+
b
3
+
c
3
−
3
a
b
c
=
(
a
+
b
+
c
)
3
−
9
(
a
b
c
)
−
3
(
a
2
b
+
a
2
c
+
a
b
2
+
b
2
c
+
a
c
2
+
b
c
2
)
a
3
+
b
3
+
c
3
−
3
a
b
c
=
(
a
+
b
+
c
)
3
−
9
(
a
b
c
)
−
3
(
a
2
b
+
a
2
c
+
a
b
2
+
b
2
c
+
a
c
2
+
b
c
2
+
3
a
b
c
)
+
9
a
b
c
a
3
+
b
3
+
c
3
−
3
a
b
c
=
(
a
+
b
+
c
)
3
−
3
(
a
+
b
+
c
)
(
a
b
+
a
c
+
b
c
)
a
3
+
b
3
+
c
3
−
3
a
b
c
=
[
a
+
b
+
c
]
[
(
a
+
b
+
c
)
2
−
3
(
a
b
+
a
c
+
b
c
)
]
a
3
+
b
3
+
c
3
−
3
a
b
c
=
(
a
+
b
+
c
)
(
a
2
+
b
2
+
c
2
−
(
a
b
+
a
c
+
b
c
)
)
Also, there was a wrong substitution in the wrong formula that made the answer right. ( a + b + c ) 2 = 2 but 1.
Log in to reply
@Roman Frago and @Ajit Deshpande Thank you very much for your concern, I just overlooked the mistake though. I have edited them already. I think that's why some people are wondering where did I get these identities.
I take it you cannot assign "a" "b" and "c" values that satisfies the equations as the formulas will not equate on power 2 and 3 to answers 2 + 3, closest I am getting without messing around is -.1945, -.1945 + 1.389 resulting in 2.004982 + 2.665111, any adjustment to the ratios only narrows the ration making achieving a result of 2 + 3 impossible?????
The value required is just e 3 e 2 , where e k is the k th elementary symmetric polynomial which can be found out by recursively using Newton's Identities as stated by Daniel.
Log in to reply
Can you tell us more what e1, e 2 means ?
Log in to reply
If the roots of a degree n polynomial are r i 1 , r i 2 , … , r i n , then we define e k as,
e k = 1 ≤ i 1 < i 2 < ⋯ < i k ≤ n ∑ ⎝ ⎛ t = 1 ∏ k r i t ⎠ ⎞ ∀ 1 ≤ k ≤ n
As an explicit example, for a quartic polynomial with roots a , b , c , d , we have,
e 1 = a + b + c + d e 2 = a b + a c + a d + b c + b d + c d e 3 = a b c + a b d + a c d + b c d e 4 = a b c d
Log in to reply
@Prasun Biswas – Very well explained............ Brilliant
The first thing that I did was rewrite the problem. a − 1 + b − 1 + c − 1 = a 1 + b 1 + c 1 = a b c b c + a b c a c + a b c a b = a b c b c + a c + a b Next, I manipulated the original equation to find a value equivalent to bc+ac+ab and another one equivalent to abc. a + b + c = 1 ( a + b + c ) 2 = 1 2 ( a + b + c ) ( a + b + c ) = 1 a ( a + b + c ) + b ( a + b + c ) + c ( a + b + c ) = 1 a 2 + a b + a c + a b + b 2 + b c + a c + b c + c 2 = 1 a 2 + b 2 + c 2 + 2 a b + 2 b c + 2 a c = 1 ( a 2 + b 2 + c 2 ) + 2 a b + 2 b c + 2 a c = 1 The expression in parenthesis is the second equation we were given; therefore, 2 + 2 a b + 2 b c + 2 a c = 1 2 a b + 2 b c + 2 a c = − 1 a b + b c + a c = − 2 1 There, we have the expression for the numerator. The denominator is a little more involved. a + b + c = 1 ( a + b + c ) 3 = 1 3 ( a + b + c ) ( a + b + c ) 2 = 1 From the previous part we know that, ( a + b + c ) 2 = 2 + 2 a b + 2 b c + 2 a c Therefore, ( a + b + c ) ( 2 + 2 a b + 2 b c + 2 a c ) = 1 a ( 2 + 2 a b + 2 b c + 2 a c ) + b ( 2 + 2 a b + 2 b c + 2 a c ) + c ( 2 + 2 a b + 2 b c + 2 a c ) = 1 2 a + 2 a 2 b + 2 a b c + 2 a 2 c + 2 b + 2 a b 2 + 2 b 2 c + 2 a b c + 2 c + 2 a b c + 2 b c 2 + 2 a c 2 = 1 Combine like terms and strategically place parentheses: 6 a b c + ( 2 a + 2 b + 2 c ) + ( 2 a 2 c + 2 a 2 b ) + ( 2 a b 2 + 2 b 2 c ) + ( 2 b c 2 + 2 a c 2 ) = 1 6 a b c + 2 ( a + b + c ) + 2 a 2 ( b + c ) + 2 b 2 ( a + c ) + 2 c 2 ( a + b ) = 1 6 a b c + 2 ( a + b + c ) + 2 a 2 ( a + b + c − a ) + 2 b 2 ( a + b + c − b ) + 2 c 2 ( a + b + c − c ) = 1 Substitute 1 for every a+b+c that appears (first equation given). 6 a b c + 2 ( 1 ) + 2 a 2 ( 1 − a ) + 2 b 2 ( 1 − b ) + 2 c 2 ( 1 − c ) = 1 6 a b c + 2 + 2 a 2 − 2 a 3 + 2 b 2 − 2 b 3 + 2 c 2 − 2 c 3 = 1 6 a b c + 2 + 2 a 2 + 2 b 2 + 2 c 2 − 2 a 3 − 2 b 3 − 2 c 3 = 1 6 a b c + 2 + 2 ( a 2 + b 2 + c c ) − 2 ( a 3 + b 3 + c 3 ) = 1 Take a look at the second and third given equations and substitute. 6 a b c + 2 + 2 ( 2 ) − 2 ( 3 ) = 1 6 a b c + 2 + 4 − 6 = 1 6 a b c = 1 a b c = 6 1 There, we have an expression for the denominator. Now we plug them back in. a b c b c + a c + a b = 6 1 − 2 1 = − 3
Nice approach for the solution for those who don't know the identities...like me
nice solution
I solved the problem this way
While a bit long, this solution was really easy to understand. Great job!
Squaring the first equation: a 2 + b 2 + c 2 + 2 ( a b + a c + b c )
but a 2 + b 2 + c 2 = 2 .
So a b + b c + a c = − 2 1 [ 4 t h equation]
Multiplying the first and second equation: a 3 + b 3 + c 3 + a b 2 + a c 2 + a 2 b + b c 2 + a 2 c + b 2 c = 2
but a 3 + b 3 + c 3 = 3
so a b 2 + a c 2 + a 2 b + b c 2 + a 2 c + b 2 c = − 1 [ 5 t h equation]
Multiplying the first and fourth equation: a b 2 + a c 2 + a 2 b + b c 2 + a 2 c + b 2 c + 3 a b c = − 2 1
but a b 2 + a c 2 + a 2 b + b c 2 + a 2 c + b 2 c = − 1
so a b c = 6 1
a − 1 + b − 1 + c − 1 = a 1 + b 1 + c 1 = a b c b c + a c + a b = 6 1 − 2 1 = − 3
Oh, what a creative solution out there :)
Oh! Nearly the same way I solved it! Great job!
Great solution!!, 😊😊😊😎😎
We have to only remember two formulas i.e. [ a + b + c ] 2 = a 2 + b 2 + c 2 + 2(ab +bc +ca) and a 3 + b 3 + c 3 - 3abc = (a + b + c)( a 2 + b 2 + c 2 - ab -bc -ca). By these two formulas we can easily equate the answer.
Subtracting the 1st equation from the 2nd:
a ( a − 1 ) + b ( b − 1 ) + c ( c − 1 ) = 1 --- ( 1 )
Subtracting the 2nd equation from the 3rd:
a 2 ( a − 1 ) + b 2 ( b − 1 ) + c 2 ( c − 1 ) = 1 --- ( 2 )
From equation 1, three equations can be deduced:
- a − 1 = − ( b + c )
- b − 1 = − ( a + c )
- c − 1 = − ( a + b )
Doing the necessary substitutions with the equations above into equation ( 1 ) and ( 2 ), we get:
a ( b + c ) + b ( a + c ) + c ( a + b ) = − 1 --- ( a ) a 2 ( b + c ) + b 2 ( a + c ) + c 2 ( a + b ) = − 1 --- ( b )
Subtracting the equation (a) from (b), expanding, cleaning up and factorising:
6 a b c + a 2 ( b + c ) + b 2 ( a + c ) + c 2 ( a + b ) = 0
Therefore,
a b c = 6 1
Now with the 1st equation, by doing the necessary multiplications we can get
a b + b 2 + b c = b
a 2 + a b + a c = a
a c + b c + c 2 = c
Adding up and simplifying,
a + b + c = a 2 + b 2 + c 2 + 2 ( a b + b c + a c )
Which reduces to a b + b c + a c = 2 − 1
Now we have all the information that we need. The equation that we want to find the value of can be written as
a b c a b + a c + b c
Thus the value is − 3
I did by this way
Because
ab+bc+ca = [(a+b+c)^2-(a^2+b^2+c^2)]/2 = [1^2-2]/2 = -1/2
and
a^3+b^3+c^3-3abc = (a+b+c)(a^2+b^2+c^2-ab-bc-ca)
<=> 3-3abc = 1*(2+1/2),
<=> abc = 1/6,
it follows that
1/a+1/b+1/c
= (ab+bc+ca)/(abc)
= (-1/2)/(1/6)
= -3.
I wanted to use Newton's sums in order to solve this problem. So, let's define: e 1 ≡ a + b + c , e 2 ≡ a b + b c + c a , e 3 ≡ a b c . The first three Newton's sums, the ones given by the problem, are thus: p 1 ≡ a + b + c = e 1 , p 2 ≡ a 2 + b 2 + c 2 = e 1 p 1 − 2 e 2 , p 3 ≡ a 3 + b 3 + c 3 = e 1 p 2 − e 2 p 1 + 3 e 3 . Since p 1 = 1 , p 2 = 2 , p 3 = 3 , we can easily determine e 1 = 1 , e 2 = − 2 1 , e 3 = 6 1 . Now, a − 1 + b − 1 + c − 1 = e 3 e 2 , and so we find the result a − 1 + b − 1 + c − 1 = − 3 ,
1 = ( a + b + c ) 2 = 2 + 2 ( a b + a c + b c ) ⟹ 2 − 1 = a b + a c + b c
1 = ( a + b + c ) 3 = 3 + 3 ( a b + a c + b c ) ( a + b + c ) − 3 a b c ⟹
− 2 = 2 − 3 − 3 a b c ⟹
− 4 = − 3 − 6 a b c ⟹ a b c = 6 1
∴ a 1 + b 1 + c 1 = a b c b c + a c + a b = − 3 .
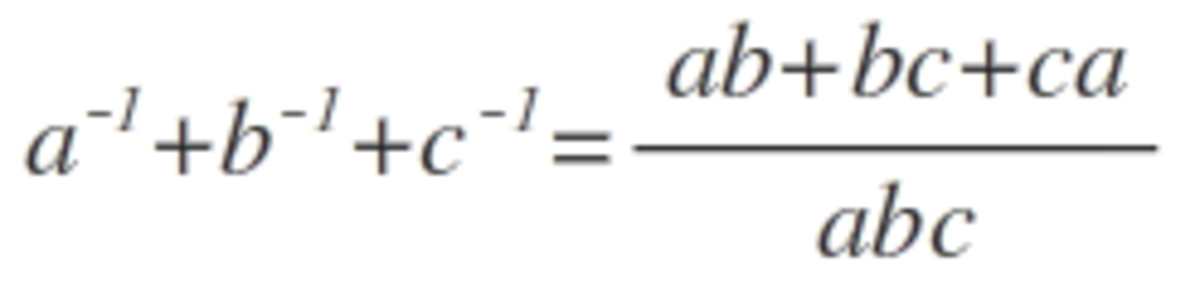
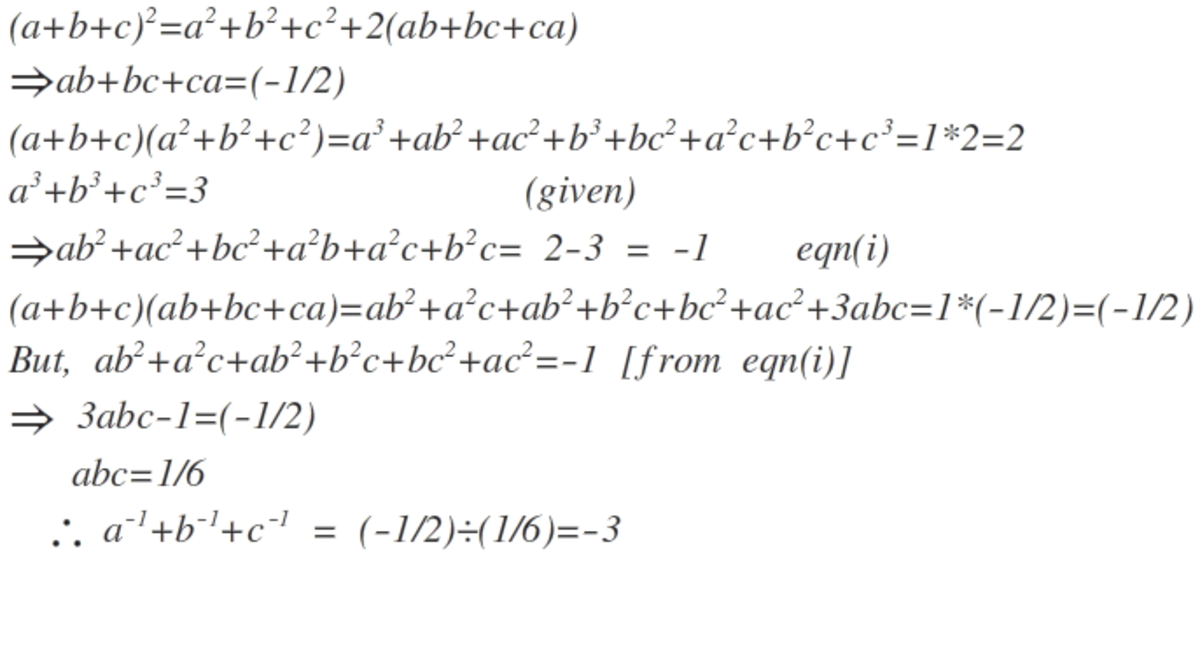
a − 1 + b − 1 + c − 1 can be written as a b c a b + a c + b c
And we have a b + a c + b c = 2 1 [ ( a + b + c ) 2 − ( a 2 + b 2 + c 2 ) ]
⇒ a b + a c + b c = 2 1 ( 1 − 2 ) ⇒ a b + b c + a c = 2 − 1
From the identity
a 3 + b 3 + c 3 − 3 a b c = ( a + b + c ) [ ( a 2 + b 2 + c 2 ) − ( a b + a c + b c ) ]
⇒ 3 − 3 a b c = 1 ( 2 + 2 1 ) ⇒ a b c = 6 1
Therefore: a − 1 + b − 1 + c − 1 = a b c a b + a c + b c = 6 1 2 − 1
⇒ a − 1 + b − 1 + c − 1 = − 3