The pentagons are not regular anymore, does it change anything?
An infinite plane can be tiled using identical triangles, quadrilaterals, or hexagons with no overlaps and no gaps.
Is it possible to tile an infinite plane using identical pentagons?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Lovely solution - made me laugh out loud!
But shapes needs to be identical!!
Log in to reply
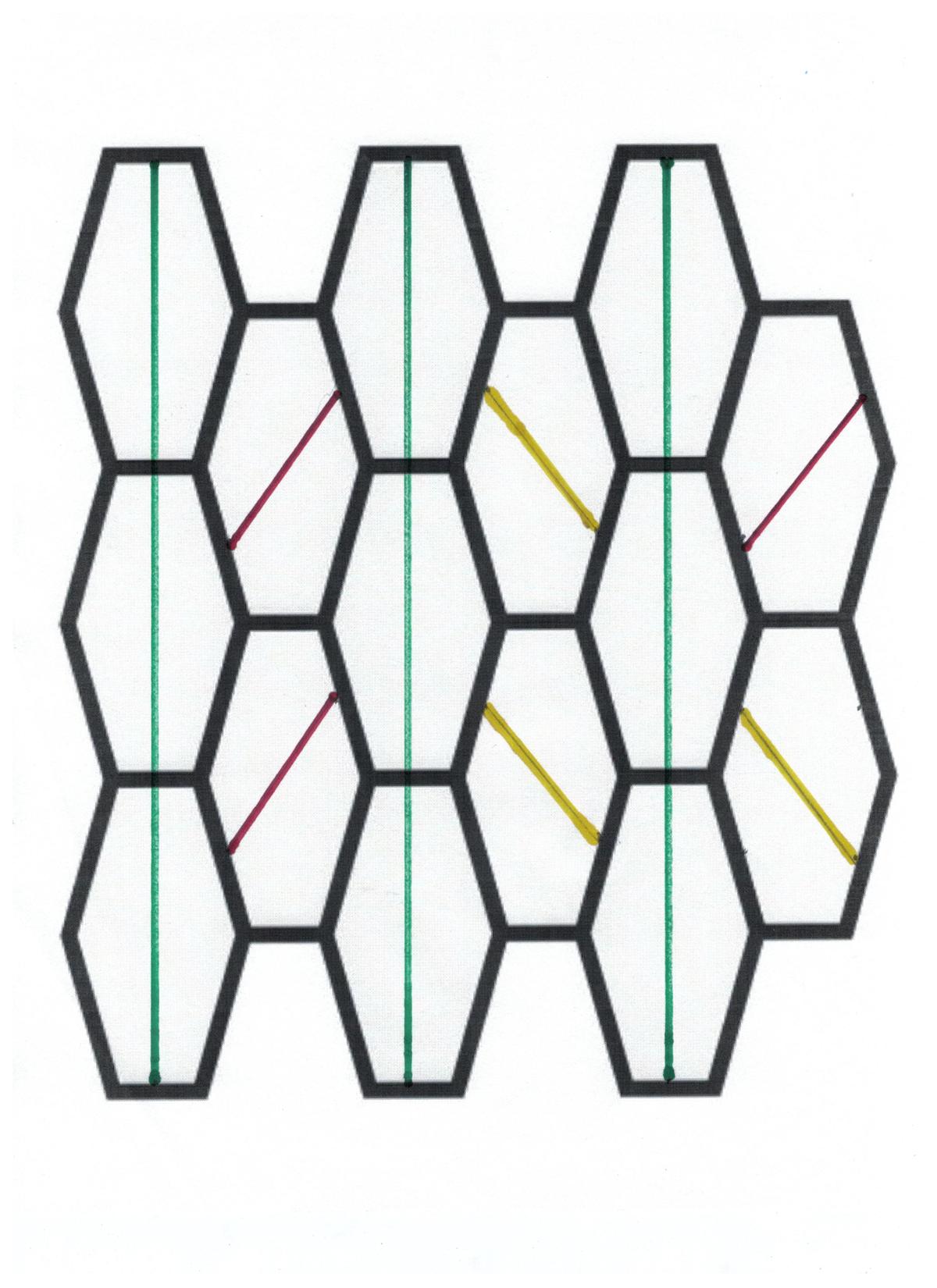
I gave three color choices, any one of which will yield an identical shape for the color (but not all the same from color to color). Tile the infinite plane with all green ones, OR all red ones, OR all yellow ones. The example is simply a display case to choose from. :)
His solution is correct, it's just the diagram that's not the nost accurate representation.
Log in to reply
A diagram from dinasour days, using straight edge and magic marker! I assume that the criticism from Prince Kumar had to do with the three examples I used, so that they did not cover the infinite plane with a single pentagonal shape. My intent, of course, was to offer a display case from which to pick your favorite pattern. 😁
Excellent.
This was really creative!
the hexagons are identical the pentagons are not cheezy
This is also a correct solution. Those who are saying that the pentagons are not identical, I understand your doubt. There are two possible solutions given in the diagram.You can choose either one, that is, you can either cut the pentagons through the vertical lines to create identical pentagons or through the the lines via the other pair of parallel lines of the pentagon. Both ways are part of the same solution set but are different solutions. Hope I have made it sufficiently clear.
Log in to reply
Mukund Choudhary - Exactly! It was easier for me to post one diagram as a "display case" of possible solutions for people to see all at once. I have edited the description. Thanks.
Any bisector of the hexagon (line thru the center) produces 2 identical (non-equilateral) pentagons.
Question is stated a bit vague, by default one think of a pentagon as a regular pentagon, which you can't tile the flat surface with...
Log in to reply
Alex P - The definition of a regular polygon (which I am sure you know; I'm just repeating for sake of discussion) is: "A polygon is regular when all angles are equal and all sides are equal." None of the three examples shown in the problem consists of regular polygons (the triangles "might be," but they really look isosceles). The terms of the problem, which says "identical," and the three irregular examples are enough to make the question clear.
Log in to reply
Probably most of people that get this question wrong are deceived by assuming a regular pentagon. The image in the question is distorted (you can tell by the line's width). If the image had the correct ratio, the examples would be regular geometric shapes (obviously except the parallelogram). Actually, to consider irregular polygons in such a question is a little bit stupid since you can fill a plane with almost any irregular polygon such as pentagons, polyominoes and in fact almost any kind of geometric shape.
Log in to reply
@Rafæl Couto – Funniest thing I've read today. Thanks!
I misunderstood the question to mean all sides must be equal for a pentagon! Didn't think broadly enough:)
a pentagon is a 5 sides geometric form, not 6 that is called an HEXagon
Log in to reply
Very good. What does that have to do with this particular problem?
Just cut each of the field filling hexagons into 2 identical, but NOT equilateral pentagons.
Albert Fishers point is that if you divide these hexagons in half "mid-side to mid-side" like he did, you would get identical pentagons.
Log in to reply
Simon Simon - Exactly! Very perceptive. Thank you.
Oops! I made the mistake of extrapolating/presuming the simplicity of the equilateral & consistent shape solutions available for the mentioned exemplars as a rule for pentagons. Of course it might be argued that circles of infinitely variable size can fill a field too (either 1 or an infinite number, infinitely small).
expain clearly
If you have to cut the hextagon in half to complete the plane, then you no longer have identical hextagons. You now 2 different shapes and one is not a hextagon anymore.
There's "only" 15 possible irregular pentagons that will tile the plane, but a few years ago it was said that there was "only" 14. The last one (bottom right) was discovered in 2015.
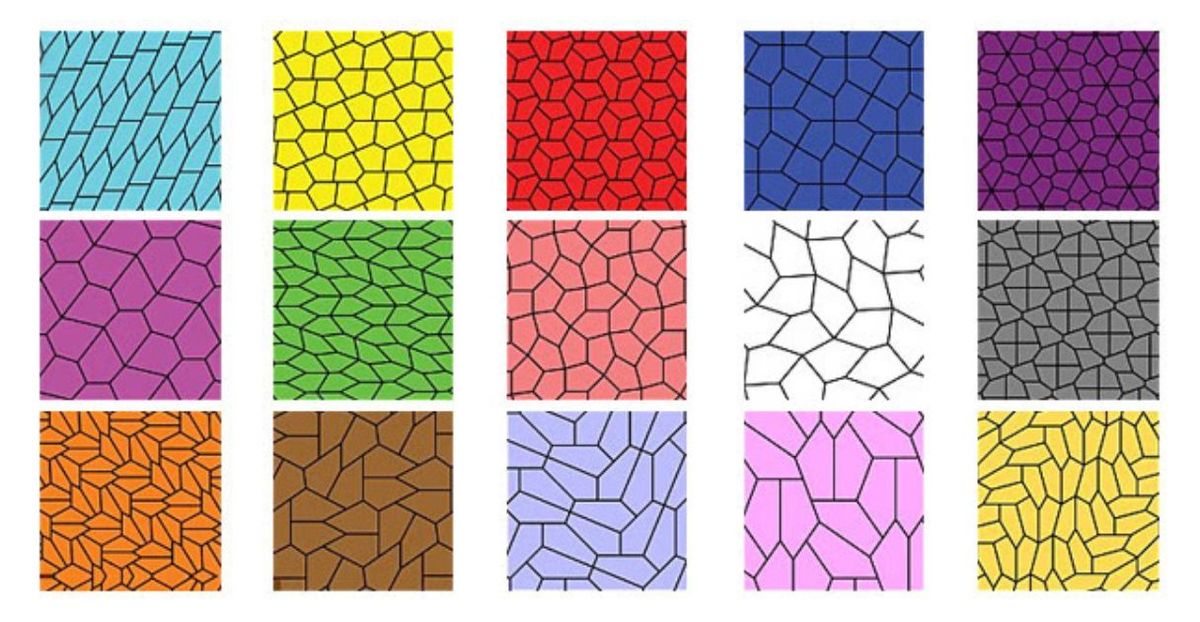
Try to see if you can figure out what are the angles of each irregular pentagon by looking at the examples of how they may tile the plane. For example, let a , b , c , d , e be the angles of the last example, where a is obviously 9 0 and the rest follows clockwise (or counterclockwise). Then we have the following equations:
2
a
+
1
8
0
=
3
6
0
2
c
+
d
+
e
=
3
6
0
2
b
+
c
=
3
6
0
b
+
2
e
=
3
6
0
2
d
+
a
=
3
6
0
From this, we have the angles ( a , b , c , d , e ) = ( 9 0 , 1 5 0 , 6 0 , 1 3 5 , 1 0 5 ) \
Here's one with non-convex pentagons

Nice solution.
I was thinking it should be possible with a non-convex pentagon. Is this possible?
It was also proven in the same paper that there cannot be any more convex pentagons that satisfy, though it was done by brute force.
So cool. I think it’s time to re-tile my kitchen!
I thought it was only applied to regular polygons!
I thought these 15 cases were missing the simple one drawn by @Albert Fisher above. However, it turns out that some of these 15 have degrees of freedom, and his solution is a semi-regular example of case 1.
For more info see https://en.wikipedia.org/wiki/Pentagonal_tiling
Can't the concave angle be varied in between 0 and 180 deg, by rotating the adjacent segment around its midpoint, and adjusting the length of it and its neighbors to fit? Maybe you meant something else by .... I think you can do anything you want with the lengths & angles, as long as you keep the line intersections intact & don't hide the 5th side with 0 or 180 deg.
I don't understand what "identical" means in the question. Rotation is obviously allowed, but I'm not sure about flipping. Some of your solutions involve flipping. Thanks for the solution.
Log in to reply
Congruent figures allows flipping, i.e., mirror images can be used.
I get you showing these but I could have used the Internet too - what’s the point? Is there a mathematical solution rather than trial & error or google?
Log in to reply
Albert Fisher provided a mathematical solution. Sometimes in mathematics, it takes a while to come up with all the possible solutions and their classification.
Awesome ! Thank you Michael Mendrin 👍. But is the last example in the bottom left surposed to be a hexagon at first place ? I am asking because it looks like a heptagon to me ? The middle one from the far right looks more like an octagon while the one on top of it looks overwhelmingly “multi-sided”. What is going on? Would you help ?
Log in to reply
Okay, I'm confused... how are you counting up the sides of the tiles? Remember, one can flip over a tile and use its mirror image, so that when you put two of them together, it forms a heptagon. But it's still 2 pentagons put together.
Awesome explaining and examples!
This is one solution, which I had in my mind at first.
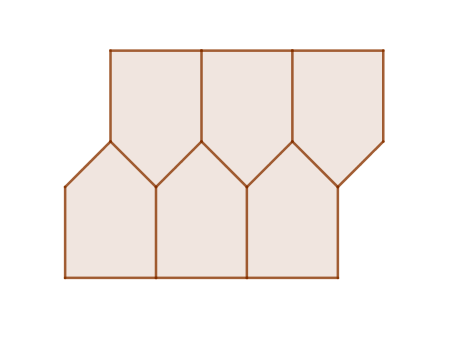
You silly gits. The equation does not state whether an infinite number of tiles were available.
Log in to reply
You shouldn’t call someone silly guts. They learnt and that is all that matters,
I wonder how many other people had this as first thought too, it's even similar to @Michael Mendrin solution top left.
This exactly the picture I had in mind as well. My question is, what restrictions are required to tile the plane with identical pentagons? 180° symmetry?
I don't understand, why is this not a legitimate solution?
I daresay that the residents of Cairo may have found this problem too easy!
Many streets in Cairo are paved with identical irregular pentagons; the design is aptly named Cairo pentagonal tiling.

Neat. A real world example.
if you have trouble with the gap left, top and bottom or/and right and left, mind you can fold the plane into a toric shape

Make a Pentagon with 5 sides the same. The angle at each corner is 360/5. So 5 of them will be 360. Done
But the sum of the angles in pentagon is 540.
If you are talking about tiling regular pentagons, then it's actually impossible to tessellate them.
For a regular pentagon if you draw lines from the vertices to the center the central angle will be 72 degrees. That makes the two base angles sum to 108 degrees. Fortunately each vertex consists of two base angles. 360 degrees divided by 108 degrees is 3 1/3, so unsuitable for tessellation.
No, the angle at each would be 108.
There is also the rather beautiful Penrose tiling with equilateral but not equiangular pentagons (concave!) - remarkable because it is infinitely non repeating (aperiodic) as it covers the plane. Thank you Martin Gardner for that and many other mathematical wonders
Yes. Simply cut a hexagon in half, mid-side to mid-side, forming two identical pentagons. There are several ways to make the cut. This is a "display case" with several patterns to choose from. Tile the infinite plane with all greens, OR all reds, OR all yellows