The popular puzzle revisited!

Number Theory Level 4

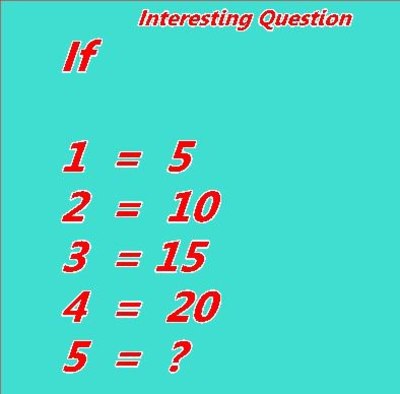
The image shows a popular puzzle, which can be seen frequently online. In fact, the statement of the problem doesn't make sense from the mathematical perspective. But I'll dive it a little deeper.

What the designer of the problem really means is to define a sequence $\{a_n\}$ , so that:

$a_{n}=\begin{cases} k , \exists k<n\ (k \in \mathbb N^+), a_k=n \\ 5n , \textup{otherwise} \end{cases}$

Find $\displaystyle \sum_{k=1}^{2020} a_k$ .

The answer is 8567810.

4 solutions

Alexander Shannon
Jul 10, 2020

1- $a_k=5 \cdot k$ iff $5 \nmid k$ or $25|k$

2- $a_k= \frac{ k}{5}$ iff $5| k \ , \ 25 \nmid k$

Based on the deductions above and using a version of Inclusion-Exclusion principle ,

$\sum_{k=1}^{2020}a_k= 5 \sum_{k=1}^{2020}k \ - \ 5 \sum_{k=1}^{2020/5} 5\cdot k \ + \ 5 \sum_{k=1}^{\lfloor 2020/25 \rfloor } 25\cdot k \ + \ \sum_{k=1}^{2020/5} k \ - \ \sum_{k=1}^{\lfloor 2020/25 \rfloor } 5\cdot k$

$\sum_{k=1}^{2020}a_k= 5\cdot (1+\dots+2020)-5\cdot 5 \cdot (1+\dots+404)+5\cdot 5 \cdot 5 \cdot (1+\dots+80)+(1+\dots+ 404)-5 \cdot (1+\dots +80)=8631410$

BTW, dont dive too deep, you may hit your head against the bottom!

What about multiples of $5^3$ and and multiples of $5^4$ ?

David Vreken - 11 months, 1 week ago

I think they fit into either of the categories 1 or 2. don't they?

Alexander Shannon - 11 months, 1 week ago

As one example, your statements would put $k = 125$ in category $1$ , which would make $a_{125} = 625$ . However, it should be $a_{125} = 25$ , because $a_{25} = 125$ .

David Vreken - 11 months, 1 week ago

@David Vreken – Now I get your point, that is correct. Then, my solution is wrong, which probably makes the final answer wrong. You are such an early bird anyways!

Alexander Shannon - 11 months, 1 week ago

@Alexander Shannon – Oh, I think I've got the same problem. I will post a revised program here.

Alice Smith - 11 months, 1 week ago

@Alice Smith could you please share with us the way you got the answer?

Alexander Shannon - 11 months, 1 week ago

OK, I've posted the revised version of it:)

Alice Smith - 11 months, 1 week ago

Yuriy Kazakov
Jul 23, 2020

seq=set()
for k in range(1,2021):
  if k in seq:
    seq.add(k//5)
  else:
    seq.add(5*k)
print(sum(seq)) 

8567810

Laura Ruzittu
Jul 16, 2020

Using Excel.

Column A and column C : from 1 to 2020.

Column B : each cell contains the expression IFERROR(VLOOKUP(An; $B$1 : C_(n-1); 2 ; FALSE); An*5) .

D1 = sum(B1:B2020) gives the answer 8567810 .

Alice Smith
Jul 10, 2020

First: The solution is incorrect. The answer should be $\boxed{8567810}$ :

The revised Wolfram code is as follows:

    a[n_] := Module[{i, m = n}, 
      For[i = 0, {q, r} = QuotientRemainder[m, 5]; r == 0, i++, m = q]; 
      m*5^If[Mod[i, 2] == 1, i - 1, i + 1]]; 
    Table[a[n], {n, 1, 2020}] // Total

Which would get $\boxed{8567810}$ .

But David is still upset. How are u gonna make that up to him?

Alexander Shannon - 11 months ago

No worries. We've discussed that in the report, so the administrator will change the answer.

Alice Smith - 11 months ago

Good on you!

Alexander Shannon - 11 months ago

@Alexander Shannon – It's all good!

David Vreken - 11 months ago

The popular puzzle revisited!

The answer is 8567810.

4 solutions

0 pending reports