The quick brown fox and the lazy duck
A fox moving at a constant speed of s m/s wants to eat a duck that is swimming at 1 m/s in a pond. The duck can only fly when he’s on land, and the fox can’t swim.
What is the maximal value of s such that wherever the animals start, the duck can reach land without being caught by the fox?
Assumptions:
- The pond is a perfectly round circle.
- The fox can start anywhere except inside the pond, but he can never enter the pond.
- The duck must start somewhere on the pond.
- If the duck reaches the edge of the pond at the exact same time as the fox, the fox catches the duck.
- If the duck reaches land and the fox is not there, he instantly flies away and the fox loses his meal.
- The duck and the fox see each other and take decisions in real time.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
there is still a question not answered, why would the duck fly if the fox can't swim… ?
Log in to reply
hmm.... well.... it's a very uncommon species of duck which can only fly when he reaches solid ground... ;-)
Actually, I hesitated posting the problem with captain Kirk using a protective shield against a monster, but the shield also tampered with the possibility of Kirk being "beamed up" to safety. But the fox and the duck were cuter...
I don't get this. What if the fox starts a million kilometers away from the lake? Why is there a maximum speed for the fox, given that he can start at any position outside of the lake?
Log in to reply
We want the duck to escape "wherever the animals (fox and duck) start" so we expect a maximum value of s (speed of the fox) that let a chance to the duck, in any case (particularly in the worse case for the duck). To do so, we consider the case where the fox is at the edge of the lake and the duck in the center because if the duck can escape in this configuration then he can escape in any other configuration by going at first in the center then starting the freeing path.
I hope i was clear :)
sorry for the late reply (i was off-line for a while), Antoine (Diot) already made a (at least in my opinion, but hopefully in yours too) very nice answer.
My (probably not so helpful) reply would have been to break down the conditions like this:
Say a speed s is "good" if whatever the starting positions the duck escapes the fox. We are looking for the maximal "good" s . Using a scenario where the fox is miles away is not helpful because the duck will always be able to escape. So the relevant positions is those where the duck is at a disadvantage.
Speed or velocity is a VECTOR thing!! So in the statement it SHOULD HAVE BEEN mentioned that constant remains speed's MAGNITUDE!
Log in to reply
if the fox speed is constant as a vector, then he has no serious chances of catching the duck, because he would not be able to go around the pond. So basically, if you make that assumption, you could have a high speed fox lose to the duck, and you stumble on the right answer. Which is not the worse thing that could happen.
Of course I agree with you that the question is perhaps not in the strictest sense mathematically formulated, but there is a fair amount of translation one should do when considering a "text-problem".
Log in to reply
you see... it is the case of how to interpret the statement! i mean if you think of velocity as of a vector then you get one answer (and IT WAS in the list of possible answers!!!!) and if you think of velocity as of scalar then you get the other answer (which was also in the list!!) so you have two correct solutions in your hands all what's left for you to do at this moment is just GUESS what the author ment!! and that's not good!!
Log in to reply
@Nik Gibson – Well, I believe that. if you interpret velocity as a vector, you get the right answer too. Here is why:
The fox has constant velocity, so he moves only in a straight line. This means that, wherever he is on the plane there are always point on the circle which he cannot attain. Since the circle is convex, the duck can always aim for those points. Hence the fox can be as fast as you want and the duck will always win. So I just proved that with constant velocity vectors the duck wins even if the fox has infinite speed. The only answers which is reasonable in this case is "It's > π " (which is the correct answer)
This solution may not show the actual maximal value of s , but is sufficient to show that for the following strategy, the maximal value of s is greater than π :
The duck can start by swimming to the center D of the pond, and then by swimming directly away from where the fox is sitting at point F . The fox must pick a direction to chase the duck as soon as possible to catch it. Once it does, the duck should veer away from it by swimming along the arc of a circle with the same radius r as the pond and a center O such that ∠ O D F makes a right angle, to reach land at point E .
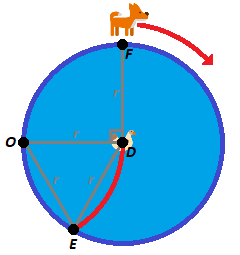
Since O D , D E , and O E are all equal to r , △ O D E is an equilateral triangle with 6 0 ° angles. Using this strategy, the total distance that the duck travels along arc D E is 3 6 0 ° 6 0 ° 2 π r = 3 π r , and the total distance that the fox travels along major arc FE is 3 6 0 ° 3 6 0 ° − ( 9 0 ° + 6 0 ° ) 2 π r = 6 7 π r , which means the fox's speed must be at least 3 π r 6 7 π r = 2 7 times faster than the duck in order to catch it.
Since the duck's speed is 1 , the fox's speed must be at least 2 7 ⋅ 1 = 2 7 in order to catch the duck. If the fox's speed is less than 2 7 , it will not catch the duck, so the maximal speed s of the fox is s < 2 7 , but since 2 7 > π , the maximal speed s can also be s > π .
I was drawing out the same thing with the duck starting in the center, but I was declared "incorrect" by a damn computer
nice solution and nice picture!
If the duck is at the center of the lake and the fox is on the perimeter, the duck can head towards the shore of the lake while keeping opposite of the center from the fox. Regardless of whether the fox moves back and forth along perimeter or runs in one direct only (counterclockwise here), the distance the duck travels until it cannot get any closer to the shore in this way is the perimeter of the semicircle, its diameter being the maximum distance from the center while still staying opposite of the center from the fox. The distance is the same whether the duck goes from
D
1
to
D
2
, or from
D
1
to
D
3
, or from
D
1
to any other point on the blue circle depending how the fox attempts to head off the duck. See the following diagram:
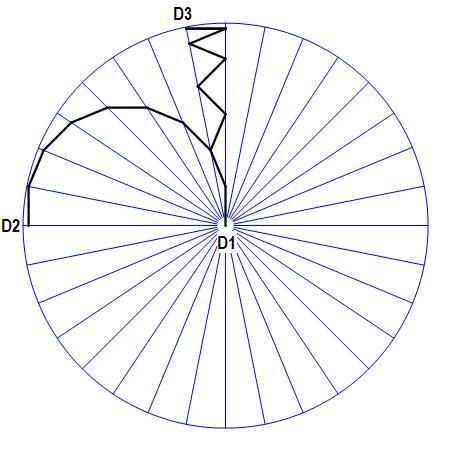 Once the duck has reached the maximum distance by this means, then the next thing the duck can do is to head straight for the shore, and hope to beat the fox that will have to run halfway around the circumference of the lake. See the following diagram:
Once the duck has reached the maximum distance by this means, then the next thing the duck can do is to head straight for the shore, and hope to beat the fox that will have to run halfway around the circumference of the lake. See the following diagram:
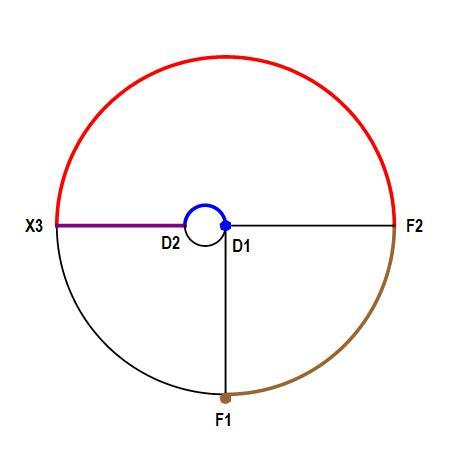 While the fox runs from
F
1
to
F
2
, the duck paddles from
D
1
to
D
2
, and then the fox has to run from
F
2
to
X
3
while the duck paddles from
D
2
to
X
3
. Let the speed of the duck be
v
d
u
c
k
=
1
and the radius of the blue semicircle be
r
s
e
m
i
c
i
r
c
l
e
=
1
also. Then we need to determine the speed of the fox
v
f
o
x
and the radius of the lake relative to the the semicircle
r
l
a
k
e
. We have the following two equations, for the two parts of the chase:
While the fox runs from
F
1
to
F
2
, the duck paddles from
D
1
to
D
2
, and then the fox has to run from
F
2
to
X
3
while the duck paddles from
D
2
to
X
3
. Let the speed of the duck be
v
d
u
c
k
=
1
and the radius of the blue semicircle be
r
s
e
m
i
c
i
r
c
l
e
=
1
also. Then we need to determine the speed of the fox
v
f
o
x
and the radius of the lake relative to the the semicircle
r
l
a
k
e
. We have the following two equations, for the two parts of the chase:
2
v
d
u
c
k
2
π
r
s
e
m
i
c
i
r
c
l
e
=
4
v
f
o
x
2
π
r
l
a
k
e
v
d
u
c
k
r
l
a
k
e
−
2
r
s
e
m
i
c
i
r
c
l
e
=
2
v
f
o
x
2
π
r
l
a
k
e
The solution leads to v f o x = π + 1 , which the fox has to exceed in order to reach the duck before it reaches the shore at X 3 . But this is not the maximum fox speed.
Per Antoine, see
this site
for details of how the duck can instead go from
D
2
to
X
3
perpendicular the line the duck, the center, and the fox are all on, for the to have to exceed
4
.
6
0
3
3
3
8
8
4
.
.
.
to get to the duck before it gets to point
X
3
on the shore. This strategy is based on the fox's realizing that it cannot afford change directions once it has become clear to him what direction the duck is heading for the shore.
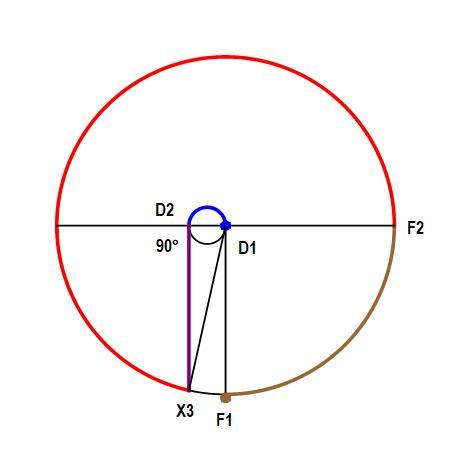
I'm not sure if this is even the maximum fox speed, though.
The first diagram is really great. Did you program it?
Also, I'm not sure whether 4.6033 is really the absolute max... the explanations on the site I linked to are somehow scarce and not quite rigorous.
Log in to reply
Same program I've been using for my other graphical work, which does have its pros and cons.
As for whether 4.6033 is really the max, this is really about game strategy, i.e., the duck should follow a path such that at any given moment it's not clear to the fox which direction it ought to take, until it becomes obvious to both that the fox will stay in one direction, after which it's about finding that final point
X
3
such that the ratios of the distances needed to travel is maximum. The tricky part to work out is the stage before that, after the duck leaves
D
2
, I don't know the answer to that one yet.
I'm not sure I understand how D2 to X3 works better unless you assume there is some delay in how the fox identifies the duck strategy. Would the fox start running clockwise at F2?
Log in to reply
I'm not sure either, Malcom. I suppose the duck can continue straight away from the fox until the fox makes its move, and then go in a perpendicular direction. This is the tricky part of the chase and evasion.
From the centre of the pond, duck can swim opposite from the fox, making a spiral, up until a radius of 1/s. At 1/s radius (red circle), duck can maintain position opposite from the fox indefinitely. There on duck can swim in straight line in one of the direction opposite from the direction the fox have chosen. Fox will start reducing the distance, but it will be too late if the speed ratio is approx. s<1.465 π , the fox will not catch the duck.
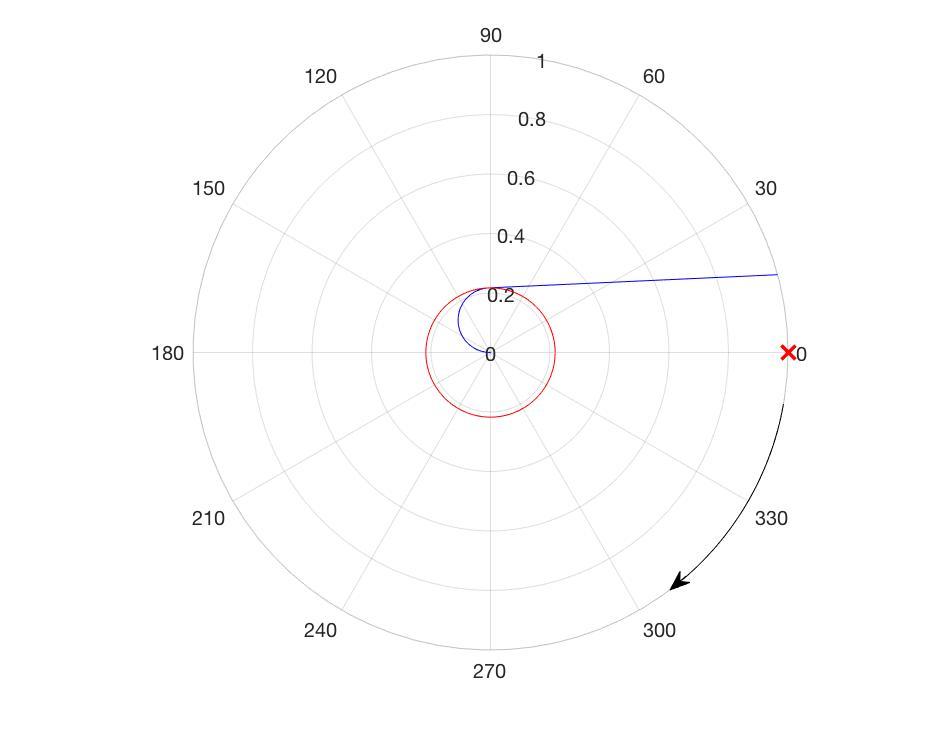
In the picture, fox start on the right, at 0 mark. Blue circle is an optimal path for the duck, given a fox that prefers clockwise direction (upon equal choice of direction). After the red circle, the fox have to commit on the direction.
EDIT: It turns out that an optimal "spiral" path that duck should follows at the beginning of the escape is actually a half circle, with radius r=1/2s. It follows from simple geometric consideration (angles duck and fox traverse).
Nice picture! Did you try to optimise the angle at which the duck leaves his first circle? the line you drew does not seem to be tangent to the smaller circle?
Log in to reply
The line is indeed tangent to the small circle. Image artefacts or optical illusions might cause one to believe otherwise (red line is plotted on top of the blue line and that might produce the effect).
How I looked at it: The worst case scenario would be the Fox being at the edge of the pond on land and the Duck being at the edge of the pond on the same side as the Fox but in the water instead. If the duck travels to the opposite end of the pond it will give the fox the longest distance to travel. I just wanted to find out if anyone else considered this as a worst case scenario. I got the question right but my math didn't end up checking out
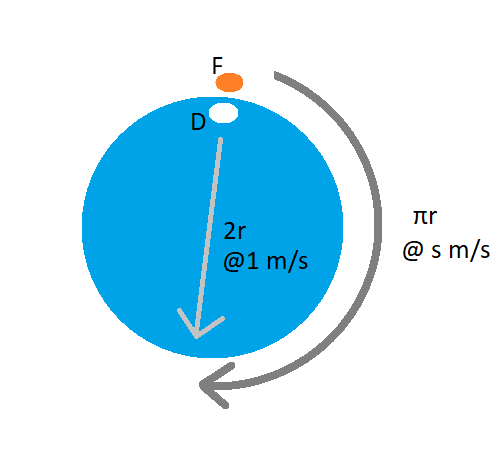
You can improve on by thinking that the duck can always travel to the centre of the pond before trying to escape. Lets say the pond had r=1 for simplicity. Duck is 1m away from the edge, whereas the Fox needs to travel π in order to reach the other side (if the duck just swims straight). For this Duck-strategy we have reached s<π because if s=π the fox will get to the edge at the same time and eat the duck.
The next step is to work out if there is a better strategy.
A simple improvement I thought of just involved the duck travelling along 2 straight lines:
Start: WLOG let the Duck be at the centre. Fox be at the bottom and goes clockwise at speed π. Let the angle clockwise from the top of the pond around the centre be θ, and D(θ) ( and F(θ) ) be the distances the duck (and Fox) are away from the edge at angle θ from centre.
Step 1: Duck moves 1/2 up. Fox moves π/2 around the pond. D(θ)=sqrt(5 - 4cos(θ))/2. cos(θ) > 1-(θ^2)/2. So D(θ) < sqrt(1+2θ^2) /2 . Using binomial expansion D(θ) < 1/2 [ 1+θ^2 ]. F(θ)=π/2+θ. In the time for the Duck to reach point θ the Fox travels π/2[ 1+θ^2 ].
Step 2: Letting θ=1/π. The fox travels π/2 + 1/(2π) < F(1/π) = π/2 + 1/π. So the Duck survives. If the Fox travels at speed π+ϵ for sufficiently small ϵ>0, the duck still survives. So s>π
Log in to reply
Seems to me that we might be able to define the quickest path for the duck by (finding where the minimum time from when the spiral motion of the duck goes to a straight line toward the edge of the pond while the fox is 180 degrees from the duck) creating an equation defining the total time it takes to traverse both the spiral and linear path(s) for the duck, and setting the 1st derivative to zero and solving?
First, one can assume that the prey begins at the center of the circle and the monster on the boundary. This case encompasses the worst-case scenario: if the prey is not in the center, then it can go to the center; if the predator is not on the boundary of the circle, then it's only better for it to be on the boundary.
The answer is not π or < π !
A first thought of many (including me) is to say the answer is π . This corresponds to the prey simply running for the point opposite to the predator on the other side of the pond. This turns out to be wrong.
Here is a better strategy. Decompose the motion of the prey (and predator) as radial and angular. Note that when the prey is closer to the center a small speed is sufficient to get a large angular speed. However the predator has always a fixed angular speed (he could choose to go clockwise or counterclockwise, but everything less is useless).
The prey starts to run to some point on the border (and the predator will start to run around the circle). As long as the prey is inside a smaller circle of g 1 the radius, it may have a higher angular speed than the predator. This means it can use parts of its speed to move radially until it gets as close as possible to this radius all the while having the predator on the opposite side of the circle.
After a very long time, being as close as desired to the circle of radius g 1 the prey can try to dash for the point opposite the predator.
This means that the prey has 1 − g 1 time units to the boundary while the predator would need g π to reach that point. ⟺ ⟺ 1 − g 1 g − 1 < π g < π + 1 < g π This shows that as long as g < π + 1 the prey can win. So the answer is I t ’ s $ > \pi $ .
Now obviously, you can still improve upon that later strategy (the prey can re-adjust the point on the edge of the pond at which it is aiming, see below). The actual maximal speed is [according to the reference] about ≈ 4 . 6 . See this site for details.
Another strategy.
Another strategy is that the duck aims [at first] for the point opposite the fox on the edge. The fox then starts to run either clockwise or counter-clockwise. When the duck has overcome half the radius, he can start to swim in a different direction (his path gets longer, but the path of the fox gets even longer). It turns out that if he then makes an angle (w.r.t. his current direction) of ≈ 3 7 ° , he can beat any fox with a speed g < 3 . 3 . It's far from being the best strategy, but it's still sufficient to see that the answer is not ≤ π .
One can try to optimise the moment at which the duck should go in a different direction and the angle of that direction. (e.g. if you go for a third of the radius and an angle of ≈ 2 6 ° you can beat speeds g < 3 . 5 ).