The radius of a circle
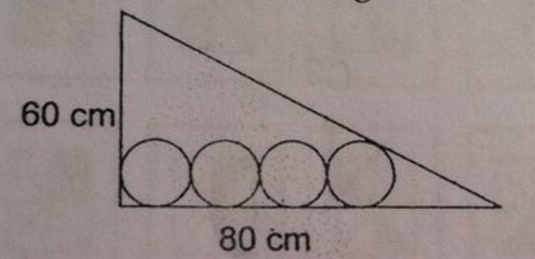 The four circles of same radius are included into right triangle as shown in the above figure. What is the radius of a circle?
The four circles of same radius are included into right triangle as shown in the above figure. What is the radius of a circle?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
Is level 1 supposed to be the easiest? This does not seem like a level 1 question. It's hard, is what I'm saying. Not impossible, but definitely not easy.
Log in to reply
I agree with you. If this question wasn't multiple choice then it would probably be level 3, but of the four answer options provided the only reasonable one is 8 cm, so it makes for a fairly easy guess.
You didn't explain how you got the 100/80 to find the distance between the top of the two triangles, it makes sence that we can find that value based off of the two hypotenuse being the distance away from eachother equal to the radius of the circles. But you never went over how you know the value will be 100/80 r
Dude coulnt understand.can u draw the diagram and share the pic pls
Imagine a similar triangle, which height is the diameter of the last circle, then the base of the triangle must be 80-7r (r: radius) // y: height and x: base, then we know by similarity that y: 6x/8, x: 80-7r , and y: 2r, we find x in the equation and it equals to 22.0689 then y: 16.55 and therefore the radius is 8.2758
The reason your answer is slightly more than the true answer is that the point of tangency of the rightmost circle with the hypotenuse is not at the height of that circle, and thus the triangle you are trying to describe is not right angled, therefore not similar. It works as an approximation though.
AB = 80; AC = 60; BC = 100 (this is a Pitagoric triangle!) Area of the triangle ABC = (AB x AC)/2 = (60 x 80)/2=2400 Consider the point D as the center of the circle closest to the vertex B. The aforementioned area is also the sum of the areas of the triangles ABD, BCD, and ACD. Note that: Height of the triangle ABD = r; Height of the triangle BCD = r; and Height of the triangle ACD = 7r. Therefore: (80 x r)/2 + (100 x r)/2 + (60 x 7r)/2 = 2400; 40r + 50r + 210r = 2400; 300r = 2400 and r=8.
This question should not be Level 1 for about 25 points.
Tan 2 Q = 60/ 80 = 3/ 4 = 2 t/ (1 - t^2) where t = Tan Q.
3 t^2 + 8 t - 3 = 0 => (3 t - 1)(t + 3) = 0 => t = 1/ 3 as Q is positive.
Tan Q = t = r/ x = 1/ 3 => x = 3 r.
7 r + 3 r = 80 => r = 80/ 10 = 8
Answer: 8 cm
All I did was realize that at least one more full circle would fit across the bottom if it wasn't for the hypotenuse. From there you can divide 80cm by 10, number of radii in 5 circles. If it had said "not drawn to scale" I would have been wrong.
Similar to how I did it. The length taken up by circles is greater than half the length of the base. Therefore the radius must be greater than 5, as there are only 4 circles. Since there is only one option that is greater than 5, that was my answer. As you say, this solution would be wrong if the puzzle had included the rule that the diagram was not to scale.
Consider last circle touching hypotenuse
Using similarity--80-8 r/80=2 r/60
we get r=7.5 thus giving 8
can you explain that in more detail?
Log in to reply
pls see the last circle an imagine a diameter touching hypotenuse and base of triangle
Log in to reply
No, I don't understand in the similarity :(
Log in to reply
@Sensen Liong – pls read triangles and you will what is similarity
You are absolutely wrong, the answer is not 7.5, its exactly 8cm from my method.
It's just common sense really. You go through each radius and you will notice non of them are big enough except from 8
The drawing is clearly wrong. 8 cm means 10 halfs of the lengths of 5 circles, which are clearly shorter than 80cm.
You can't expect the drawing to give you the answer straight away. There are indeed 5 circles exactly to fit in the length of 80 cm for actual exact drawing. This is not considered wrong.
Form a triangle similar to the one in the diagram as follows. Let the base go from the point of tangency of the leftmost circle with the 60 cm side of the main triangle to the center of the rightmost circle. Let the hypotenuse run parallel to the hypotenuse of the main triangle from the center of the rightmost circle to the 60 cm side of the main triangle. The vertical side then runs between the points where the base and hypotenuse intersect the 60 cm side.
The base then has a length of 7 r , where r is the radius of each of the circles, and so by similarity the height of our secondary triangle has a length of 8 0 6 0 ∗ 7 r = 4 2 1 r . But we can also measure this vertical side in a second way. Since the hypotenuse of our secondary triangle is a perpendicular distance of r from the hypotenuse of the main triangle, by similarity the distance between the upper vertices of the two triangles will be 8 0 1 0 0 ∗ r = 4 5 r . Thus the length of the vertical side of our secondary triangle can also be represented by 6 0 − r − 4 5 r = 6 0 − 4 9 r , and so
4 2 1 r = 6 0 − 4 9 r ⟹ 4 3 0 r = 6 0 ⟹ r = 8 c m .