The raise of iota
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
15 solutions
why did u attach 'k' with pi?? k has to be 1 or in d form 4*(n )+ 1 where n is an integer.k cannot be 2 ,3..
Log in to reply
It is because that exponential can take multiple values.
Log in to reply
If it is 2 then it becomes sin 180, which is zero. We require 4n + 1 multiples of pi by 2.
Log in to reply
@Vishnu Bhagyanath – In the next line, he has put a conditional clause to constrain the values of k to 4n+1. i.e. k = 1,5,9... for n = 0,1,2... Just another way of putting across the same point.
He did write that!
You need to be careful with complex exponentiation. There could be multiple values that i i takes on.
Log in to reply
So can you tell me how to specify them?
Log in to reply
So, more accurately, because e 2 k π i = 1 , we have i = e i 2 k π , and so i i = e i 2 2 k π = e − 2 k π , as the multiple values of the complex exponentiation.
Log in to reply
@Calvin Lin – So I was writing this solution for principle value of argument.Correct me if I am wrong .
Log in to reply
@Shivamani Patil – Since you're finding the value of i i , you should show that the all the (possible) values you've found are real numbers, instead of just showing one such value is a real number.
@Shivamani Patil – Yes, your solution applies to the principle value.
However, the question did not say "We are restricted to principle value of the argument". As such, there is the possibility that one of its values is real, while another of its value is complex.
@Calvin Lin – I don't understand why you could write that e 2 k π i = 1 . We cannot square both sides of an equation if one of them is negative, or am I missing something? Thank you
sIR, could u please explain how can i^i have multiple values ?
Can you tell me where you get that formula from? or is it like a formula?
Log in to reply
Click on the "View Wiki" button, which sends you to De Moivres Theorem .
You are 15, must be in 10th grade? I'm surprised they teach you Euler's equation in India at this level. Where I live the 10th grade syllabus doesn't comprise of Euler's equation.
Log in to reply
They didn't teach nor I have it in our syllabus. I learned it by myself.
Log in to reply
From where do you learn? Any specific website or book?
Log in to reply
@Mehdia Nadeem – I mostly learned it from online videos and articles .
Log in to reply
@Shivamani Patil – They say " Formal education earns you a living but personal education earns you a fortune." I believe this.
You don't even know India . We have world's one of the worst education system.
Calvin Lin, please mentor me . . . . . I really want to excel im math too . . . .
Log in to reply
You will excel.Slowly you will learn all concepts from wiki's ,problems and note that members post.Learn basics to have a strong foundation for advanced maths.I have a similar story of mine when I started brilliant I used to just stare at problems I didn't knew what to do,but slowly all problems,note and wikis helped me a lot.
Log in to reply
thank you so much , I will follow what you have said. I am now more motivated than before. Again, thank you so much.
Log in to reply
@Neil Ryan Manolong – Welcome brother,happy journey.
any specific book or website?
Log in to reply
For what?You mean complex numbers?
Log in to reply
not specifically complex nos., but a reply to your comment that you studied it on your own. i meant general topics out of class 10 syllabus.
Log in to reply
@Pulkit Gopalani – Mostly internet.
Log in to reply
@Shivamani Patil – i have a friend of mine who is taught things like this in coaching centers for IITJEE, so i probably thought there was such a specific book......... anyways, i will search, if i get time!(ps. i hate social science, but have to study and that is why i dont get much time to search this interesting stuff.)
Log in to reply
@Pulkit Gopalani – Me too hate Sst but economics seems interesting .There are books in markey search for books on google amd you can buy them.
@Pulkit Gopalani – Use Eulers formula. e (power ) ix= cos x + i sin x substitute x = pie/2
so e (power)i.pie/2 = cos pie/2 +i sin pie/2 = i.
now Shivamani Patils solution continues.
Maybe you should try "Complex Variables" from Mark J. Ablowitz and Athanassios S. Fokas or "Complex Analysis" from Serge Lang.
search "i^i" on google and it will give you a number, 0.20787957635, and that is a perfectly valid and real number.

This shows that i to the i is purely a real number.
Edit: for those curious about Euler

But i = e 5 i π / 2 too... thus i i = e − 5 π / 2 ... which of course does not affect the final answer... but... is a b well defined as an operation between complex numbers?
Let z = i =e^[(0.5pi).i]
Thus, using Moivre's Theorem,
z^i = (e^[(0.5pi).i] )^i
= e^-0.5pi = real number
Moderator note:
Yes, that is one of the possible values of i i . With complex exponentiation, you have to be careful with the possibility of multiple values.
i=(-1)^1/2
i^i=(-1)^1/2)^-1)^1/2)
=(-1)^1/2)^-1/2)
=(-1)^-1/4
=-(1/(1^1/4))
=-(1/1)
Which is a real number.
Something wrong...
before the last step you forgot about the minus sign. (-a)^b = [(-1)^b ]*[(a)^b] where a=1 and b=1/4.. Actually ur approach is somewhat wrong. And it seems u forcefully gave the solution..
Log in to reply
Wouldn't that still give a real number?
Log in to reply
In short, simple algebra does not apply to complex problems just like this problem which involves complex numbers.
it is giving real answer but the answer theoretically is wrong. Actually it is exponential.You have actually done it totally wrong. from the start itself,u were wrong. Actually it cant be done with simple algebra. Its got to be solved with Eulers thorem and most importantly the common mathematics skills. YOU MAY REFER to the solution which i gave
Log in to reply
@Nitin Jaitly – WHY can it not be solved with simple algebra?
Simple and great way to solve.
e^{π×i}+1=0 =>e^{π×i}=-1 Then, -1=i^{2} so e^{π×i}=i^{2} Square root, i=(e^{π×i})^{1/2}=e^{i×π/2} So i^i=e^{i×i×π/2}=e^{-π/2}, and this is a real number...
ln(i^i) = i*ln(i) = (i^2) * (pi/2) = -pi/2
i^i = exp(-pi/2)
Which is a purely real number.
Note: i=exp((pi/2)i) => ln(i)=(pi/2)i
From Euler we know e^(i pi) = -1, note i^2 = -1 hence e^(i pi / 2) = i , now if we raise this all to the power of i then we get i^i = (e^(i pi / 2))^i , who this gives us e^(i^2 pi / 2) and as i^2 = -1 then i^i = e^(-pi / 2) which approximates to 0.2079
i^(i) = (exp(ln(i)))^i ==> ( a^b=exp(b*ln(a)) )
= exp(i*(i*pi/2)) ==> ( ln(z) = ln(r) + i*arg(z) )
= exp(-pi/2) ==> ( i*i = i^2 = -1 )
By the Euler's formula: exp(i x pi/2) = cos(pi/2)+ i x sin(pi/2) = i ( where exp is the exponential function, exp(x) = e^x)
Raising both side to i, we have:
exp(i x i x pi/2) = i^i
So,
i^i = exp(-pi/2) which is a purely real number
a) ln(i^i) = i * ln(i); b) i = exp(i * pi/2); c) i * ln(i)=i * i * pi/2 = -pi/2 = "purely real"; d) i^i = exp("purely real") = "purely real"
taking i=exp(ix) ; where x is any complex number (a+ib) form
by De Moivre's theorem.....
exp(ix)= cos x+ i sin x
let, x= Π/2
exp(iΠ/2)= cos Π/2+i sinΠ/2= i ; satisfying the eqn.
i^i = exp[(i^2) Π/2] = exp (-Π/2) = 0.2078 ; a real value
for any real no. x= (2kΠ+Π/2) ;k =0,1,2,3......
i.e., exp[-(2kΠ+Π/2)]=i^i ; which gives real values
using euler's identity we can solve it to get e^pi/2 which is purely real
e^iπ=-1
=>(-1)^1/2=e^iπ/2
=>i=e^iπ/2
=>i^i=e^(iπ/2)i=e^(-π/2)=0.207879....which is a purely real number.
i^i=[cos (pi/2) + i sin (pi/2)]^i = e^[(i pi/2) (i)] = e ^ ( -pi/2) which is purely real
This solution applies for principle value of argument .You should show that it is true for all cases.
Log in to reply
ok i m going to change it this way i^i=[cos k(pi/2) + i sin k(pi/2)]^i = e^[k(ipi/2)(i)] = e ^ ( -k pi/2) which is purely real where k is like 1,5,9 i.e of the form 4 (n) +1 where n is an integer..
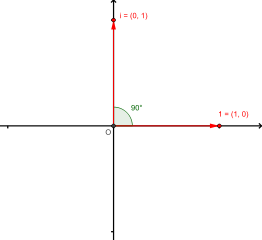

i = e i k 2 π ⇒ i i = e i 2 k 2 π = e − k 2 π which is a purely real number.
k = 4 n + 1