The sequence about the year
 1
+
2
+
3
+
⋯
+
2
0
1
2
+
2
0
1
3
+
2
0
1
4
1
2
+
2
2
+
3
2
+
⋯
+
2
0
1
2
2
+
2
0
1
3
2
+
2
0
1
4
2
=
?
1
+
2
+
3
+
⋯
+
2
0
1
2
+
2
0
1
3
+
2
0
1
4
1
2
+
2
2
+
3
2
+
⋯
+
2
0
1
2
2
+
2
0
1
3
2
+
2
0
1
4
2
=
?
Hint : 1 2 + 2 2 + 3 2 + ⋯ + n 2 = 6 1 n ( n + 1 ) ( 2 n + 1 ) .
The answer is 1343.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
13 solutions
It is a beautiful solution.
How to find a formula for finding the nth term and the sum of first n numbers?
Log in to reply
The sum of the first n numbers is given by the expression,
n(n+1)/2.
For Example, In 1+2+3, n=3 The sum of the three numbers is 3(3+1)/2=6.
For the nth term, the formula is a+(n-1)d, where a is the first term, n is the term you want to find and d is the common difference between any two terms.
For example, In 2, 4, 6, 8... To find the 20th term, a=2; n=20; d=2 (4-2);
Therefore, the 20th term is: a+(n-1)d = 2+19(2) = 40.
Can we derive formulae for findin1^2+2^2-------+n^2 =n(n+1)(2n+1)/6
Amazing. I just can not believe that I did not see it
To be honest, this is quite easy to think of this way... for there is only one EASY and obvious way to solve this problem
For those who dont have the algebraic background to solve this, this is an alternative solution: T 1 = 1 1 2 T 2 = 1 + 2 1 2 + 2 2 T 3 = 1 + 2 + 3 1 2 + 2 2 + 3 2 . . . T 1 , T 2 , T 3 , T 4 . . . 1 , 3 5 , 3 7 , 3 . . . 3 3 , 3 5 , 3 7 , 3 9 . . . ∴ T n = 3 2 n + 1 T 2 0 1 4 = 3 2 ( 2 0 1 4 ) + 1 = 1 3 4 3
How did you derived the formula 2n+1 upon 3 ???? Please tell. Didn't get it up there.
Log in to reply
When you are trying to convert a series into a formula, sometimes you have to just... see the pattern. The pattern here is rather simple though. They way Julian has this set up, he is in essence making an arithmetic sequence. You can use the formula for the nth-term on an arithmetic sequence to make a formula like this:
a n = a 1 + ( n − 1 ) d
Where a 1 is the first term and d is the difference between any two consecutive terms. Here, a 1 is 1 and d is 3 2 . So just plug in those two and simplify: a n = 1 + ( n − 1 ) ( 3 2 ) = 3 2 n + 3 1 = 3 2 n + 1
Log in to reply
But how do you know that it's an arithmetic sequence? A sequence that begins 1, 2, 3, 4 could be just the sequence of natural numbers, but without knowing any further terms of the sequence, for all you know it could be the sequence of 2 4 x 4 − 1 0 x 3 + 3 5 x 2 − 2 6 x + 2 4 for successive x .
Log in to reply
@Stewart Gordon – You never KNOW, but you can make an educated guess. And the more often it happens, the more proof you have that it is right.
@Stewart Gordon – We can always prove a sequence by induction if we really need to.
I am the 12000th solver!
W e k n o w t h a t : 1 ² + 2 ² + 3 ² + . . . + n ² = 6 n ( n + 1 ) ( 2 n + 1 ) a n d : 1 + 2 + 3 + . . . + n = 2 n ( n + 1 ) S o : 1 + 2 + 3 + . . . + n 1 ² + 2 ² + 3 ² + . . . + n ² = 2 n ( n + 1 ) 6 n ( n + 1 ) ( 2 n + 1 ) = n ( n + 1 ) 3 n ( n + 1 ) ( 2 n + 1 ) = 3 2 n + 1 F o r n = 2 0 1 4 w e h a v e : 3 2 n + 1 = 3 4 0 2 9 = 1 3 4 3 ∴ 1 + 2 + 3 + . . . + 2 0 1 4 1 ² + 2 ² + 3 ² + . . . + 2 0 1 4 ² = 1 3 4 3
We have ( n + 1 ) 3 − n 3 = 3 ∗ n 2 + 3 ∗ n + 1 Then, let A = 1 + 2 + 3 + … + 2 0 1 2 + 2 0 1 3 + 2 0 1 4 1 2 + 2 2 + 3 2 + … + 2 0 1 2 2 + 2 0 1 3 2 + 2 0 1 4 2 Then 3 ∗ ( A + 1 ) = 1 + 2 + 3 + … + 2 0 1 2 + 2 0 1 3 + 2 0 1 4 2 3 − 1 3 + 3 3 − 2 3 + 4 3 − 3 3 + … + 2 0 1 3 3 − 2 0 1 2 3 + 2 0 1 4 3 − 2 0 1 3 3 + 2 0 1 5 3 − 2 0 1 4 3 − 2 0 1 4
After cancellation we have 3 ∗ ( A + 1 ) = 1 + 2 + 3 + … + 2 0 1 2 + 2 0 1 3 + 2 0 1 4 2 0 1 5 3 − 2 0 1 5 After applying the formula of the sum of the first n positive integers we have 3 ∗ ( A + 1 ) = 2 0 1 5 ∗ 2 0 1 4 ∗ 2 1 2 0 1 5 3 − 2 0 1 5 Then we have 3 ∗ ( A + 1 ) = 4 0 3 2 So we get the value of A A = 1 3 4 3
if we calculate the first terms as : 1 1 2 = 1 = 3 3 and the second term can be written as : 1 + 2 1 2 + 2 2 = 3 5 .......... so in general : the n t h term can be represented as : 3 1 + 2 n .......... so : the 2 0 1 4 t h term is 3 1 + 2 0 1 4 ∗ 2 = 1343
Okay if you observe the series and divide it .. 1^2÷1=1 i.e. 3/3 (1^2+2^2)÷(1+2)=5/3...... .... And so on We have to find series till 2014 so we will use the 2015th odd number in numerator and 3 in denominator Which gives us 4029/3=1343 Which is the answer
the hint made the sum much more easier. The sum should have been given without a hint. Then it would be more challenging
Python:
a=0
b=0
c=1
while(c<=2014):
a+=c*c
b+=c
c+=1
print(a/b)
screwmath
= 2 X 3 X ( 1 + 2 + 3 + . . . + 2 0 1 4 ) 2 0 1 4 X 2 0 1 5 X 2 X 2 0 1 4 + 1 = 2 X 3 X 2 0 1 5 X 1 0 0 7 2 0 1 4 X 2 0 1 5 X 4 0 2 9 = 2 X 3 X 1 X 1 2 X 1 X 4 0 2 9 = 3 4 0 2 9 = 1343
1 + 2 + 3 + . . . . . . + 2 0 1 2 + 2 0 1 3 + 2 0 1 4 1 2 + 2 2 + 3 2 + . . . . . . + 2 0 1 2 2 + 2 0 1 3 2 + 2 0 1 4 2
⇔ 2 1 n ( 1 + U n ) 6 1 n ( n + 1 ) ( 2 n + 2 )
⇔ 2 1 n ( 1 + n ) 6 1 n ( n + 1 ) ( 2 n + 2 ) , f o r U n = n
⇔ 3 1 × ( 2 n + 2 )
⇔ 3 1 × ( 2 × 2 0 1 4 + 2 ) = 1 3 4 3
most people uses a direct formula for this, but i found that sometimes it is easier to do a direct approach to these kind of questions e.g. 1^2/1 = 1 = 3/3
(1^2+2^2)/(1+2) = 5/3
(1^2+2^2+3^2)/(1+2+3) = 14/6 = 7/3
(1^2+2^2+3^2+4^2)/(1+2+3+4) = 30/10 = 3 = 9/3
from these results we can see a pattern
the denominator will always be 3, while the numerator is form in a pattern; 3, 5, 7, 9, ...
so the only thing need to be done is find the pattern equation for the numerator.
for this example, the pattern can be simplify;
3, 5, 7, 9, ... = 3, (3+2), (3+4), (3+6), ...
from that, an equation to the pattern is made: 3+2(n-1).
now we need to test if the equation above will satisfy the pattern.
Testing
n | result
1 | 3
2 | 5
3 | 7
4 | 9
the equation satisfy the pattern!
therefore, the complete equation to the example is (3+2(n-1))/3
now, since the queation ends with 2014, we subtitute n as 2014.
(3+2(2014-1))/3 = 4029/3 = 1343
We can do it 1^2/1=1 (1^1+2^2)/3=1.6666666 (1^1+2^2+3^3)/6=2.3333333 So it is increasing by 0.6666667 So answer is 2014×0.6666667=1342.66 Rounding off. 1343
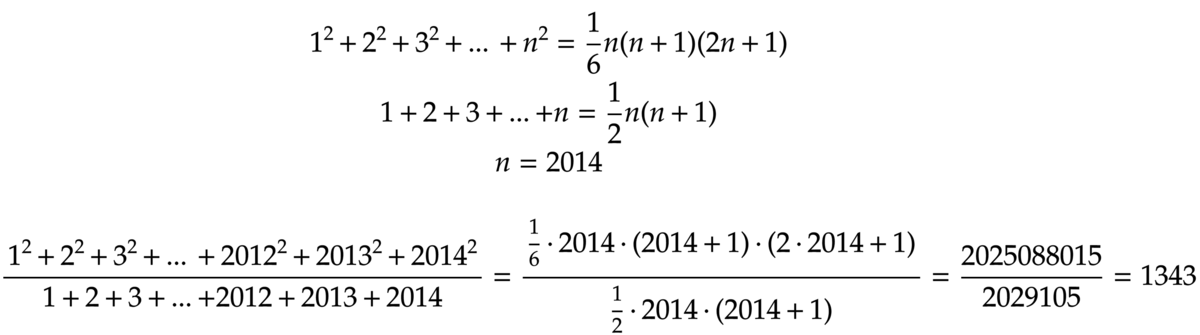
The formula for the sum of the first n positive perfect squares is
6 n ( n + 1 ) ( 2 n + 1 ) .
The formula for the sum of the first n positive integers is
2 n ( n + 1 ) .
Thus, by dividing the two quantities, we get
2 n ( n + 1 ) 6 n ( n + 1 ) ( 2 n + 1 ) = 3 2 n + 1 .
Substituting, we get
3 4 0 2 9 = 1 3 4 3 .